线索二叉树遍历

😭这个真不简单，亿点点难(●'◡'●)

首先说明：
线索二叉树包括两个方面：

• 线索化二叉树
• 遍历线索二叉树

以及TreeNode的定义:

title:TreeNode的定义

struct TreeNode
{
    char val;
    TreeNode* left;
    TreeNode* right;
    bool Lflag;
    bool Rflag;
    TreeNode(char v):val(v),left(nullptr),right(nullptr),Lflag(0),Rflag(0){}
    TreeNode(char v,TreeNode* l,TreeNode* r):val(v),left(l),right(r),Lflag(0),Rflag(0){}
}*fptr;

1. 前序

---

1.1 前序线索化二叉树(😘)

这个部分是真的简单

title:前序线索化

void pre(TreeNode* root)
{
    if(!root) return;
    
    if(!root -> left)
    {
        root -> left = fptr;
        root -> Lflag = true;
    }
    if(fptr && !fptr -> right)
    {
        fptr -> right = root;
        fptr -> Rflag = true;
    }
    fptr = root;
    if(!root -> Lflag) pre(root -> left);
    if(!root -> Rflag) pre(root -> right);
}

title:其实最重要的是下面代码的摆放位置

if(!root -> left)
    {
        root -> left = fptr;
        root -> Lflag = true;
    }
    if(fptr && !fptr -> right)
    {
        fptr -> right = root;
        fptr -> Rflag = true;
    }
    fptr = root;

由于这里是前序线索化二叉树所以顺序为主要操作->左节点->右节点

最后的最后,你要清楚线索化二叉树后,这棵树变成什么样

可以试着模拟一下最后得到的图是右边两张图,可以发现最后一个节点是不用给其后继加nullptr

因为前序遍历遍历到最后一个节点的时候它的右子树必定为空

1.2 遍历前序线索化二叉树(💩)

如果按照前面的步骤,一个遍历的思路为:

1. 首先从根节点(或者之后的右子树的根节点)开始,一直向左,访问最左节点,每次访问时输出该节点上的值(出口条件为当前点的Lflag为1)
2. 然后一直访问右节点(出口条件为该节点为nullptr,这里是整个循环的退出条件)

void preTraversal(TreeNode* root)
{
    auto cur = root;
    while(cur)
    {
        while(!cur -> Lflag)
        {
            cout << cur -> val << " ";
            cur = cur -> left;
        }
        cout << cur -> val << " ";
        cur = cur -> right;
    }
}

2. 中序(😢)

---

还好其实

2.1 中序线索化(😍)

有了前面的铺垫,这里简直送分

title:前序线索化

void pre(TreeNode* root)
{
    if(!root) return;
    
    if(!root -> Lflag) pre(root -> left);
	if(!root -> left)
    {
        root -> left = fptr;
        root -> Lflag = true;
    }
    if(fptr && !fptr -> right)
    {
        fptr -> right = root;
        fptr -> Rflag = true;
    }
    fptr = root;
    if(!root -> Rflag) pre(root -> right);
}

中序线索化二叉树,所以顺序为左节点->主要操作->右节点

一种可能得到的结果是这样的:

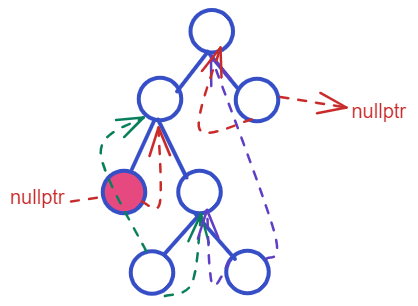
2.2 遍历中序线索化二叉树(🤔)

按照图片,我们可以总结如下:

1. 每次循环开始的时候,一直往左走,找到最左节点,并输出该点的值
2. 如果该点有后继元素,如粉红色标红区域,则持续访问后继元素并输出(其实有后继元素暴露了该点在原本的树内右儿子为空)
3. 没有后继元素,则访问右子树,开始新一轮循环

代码如下:

title:遍历中序线索化二叉树

void inTraversal(TreeNode* root)
{
    auto cur = root;
    while(cur)
    {
        while(!cur -> Lflag) cur = cur -> left;
        cout << cur -> val << " ";
        while(cur -> Rflag)
        {
            cur = cur -> right;
            cout << cur -> val << " ";
        }
        cur = cur -> right;
    }
}

3. 后序(😭😭😭)

规则实在太复杂了,先逃再说

4. 线索二叉树线索的数目

若节点数目为n，总共指针有2n个，其中连接子女的指针有n-1个(树的性质)，其余空指针都被用来当作线索，有2n-(n-1)=n+1个