二叉树非递归后序遍历

题目描述：给你一个二叉树的根节点root，返回其节点值的后序遍历
![pre1.jpg (202×317) (leetcode.com)

输入：root = [1,null,2,3]

输出：[3,2,1]

方法1.
title:双探路指针

class Solution {
public:
    vector<int> postorderTraversal(TreeNode *root) {
        if (!root) return {};
        vector<int> vec;
        stack<TreeNode *> stk;
        TreeNode *prev = nullptr;
        auto node = root;
        while (!stk.empty() || node) {
            // 1.遍历到最左子节点
            while (node) {
                stk.emplace(node);
                node = node->left;
            }
            node = stk.top(); stk.pop();
            // 2.遍历最左子节点的右子树(右子树存在 && 未访问过)
            if (node->right && node->right != prev) {
                // 重复压栈以记录当前路径分叉节点
                stk.emplace(node);
                node = node->right;      
            } else {
                // 后序：填充vec在node->left和node->right后面
                // 注意：此时node的左右子树应均已完成访问
                vec.emplace_back(node->val);
                // 避免重复访问右子树[记录当前节点便于下一步对比]
                prev = node;
                // 避免重复访问左子树[设空节点]
                node = nullptr;
            }
        }
        return vec;
    }
};

这个版本其实不太好理解。

因此来一个过渡态。。。。染色法与普通方法的过渡(┬┬﹏┬┬)
验证方法正确性

typedef pair<bool,TreeNode*> IT;
void postorder(TreeNode* root)
{
    stack<IT> s;
    TreeNode *p = root;
    while(!s.empty() || p)
    {
        while(p)
        {
            s.push({0, p});
            p = p -> left;
        }
        auto u = s.top();s.pop(); 
        bool flag = u.first; p = u.second;
        if(!flag)
        {
            s.push({1, p});
            p = p -> right;
        }
        else
        {
            cout << p -> val <<" ";
            p = nullptr;
        }
    }
}

^98f448

需要知悉：

1. 后序遍历是左->右->中
2. 遍历会遍历所有节点
3. 后序遍历事实上是表示根节点(相对于子树的概念)最后访问，这意味着我们只需要在中的位置放入答案，就能将所有的节点按照后序读入
4. 同样使用这个理解方式能读懂前序与中序[[二叉树非递归前序遍历#^{ea08fd]][[二叉树非递归中序遍历#}0ff251]]

———————————————————————————————————————————
exp1: 代码的整体框架

• 首先while(node)将左边节点全部遍历
• 然后如果已经是当前最左边，再往其右子树延申
• 如果最终遍历的一个节点既没有左子树也没有右子树(即符合左->右->中的遍历到了中)，这个时候就将其置入答案res

———————————————————————————————————————————
exp2: prev&&root指针的细节：

• root的理解方式任然可以按照之前的探路指针来理解，不过

  • root=nullptr实现了回溯(回溯的时间发生在遍历到第一个答案的位置，所以写在这里)，具体的实现方式是跳过左->右->中->左，此时中的左子树已经遍历过了，所以取root=null进行跳过

• prev指针是防止重复访问右边的子树，这一般发生在
  

———————————————————————————————————————————

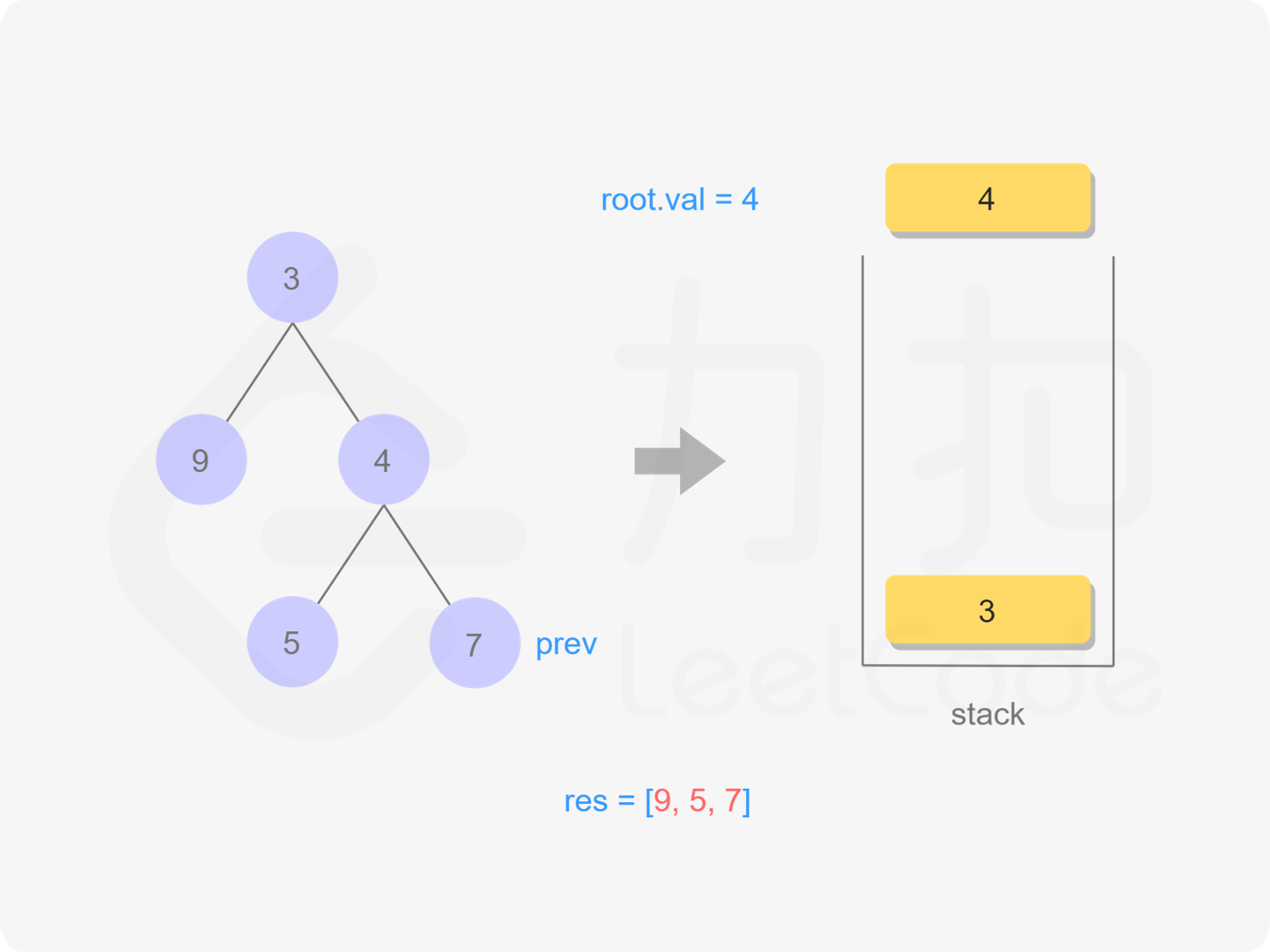
方法2：
title:万能标记法

typedef pair<int,TreeNode*> IT;
class Solution {
public:
    vector<int> postorderTraversal(TreeNode* root) {
        vector<int> res;
        stack<IT> sta;
        sta.push({0,root});
        while(!sta.empty())
        {
            auto u = sta.top();
            int flag = u.first;
            sta.pop();
            TreeNode* node = u.second;
            if(!node) continue;
            if(!flag)
            {
	            //只需要自下往上按照x序遍历的顺序写就可以了
	            sta.push({1,node});
                sta.push({0,node -> right});
                sta.push({0,node -> left});
            }
            else res.push_back(node -> val);
        }
        return res;
    }
};