面向对象第一单元总结
本文为面向对象课程第一单元“表达式求值”作业的总结,回顾并分析了我在这一单元三次作业中的代码结构、遇到的 bug 和重构经历等内容。
基于度量的程序结构分析
第一次作业
方法度量
| 方法 | 代码行数 | 认知复杂度 | 本质圈复杂度 | 设计复杂度 | 圈复杂度 |
|---|---|---|---|---|---|
| ExpressionLexer.analyze | 34 | 17 | 7 | 10 | 11 |
| ExpressionLexer.isAsciiDigit | 3 | 1 | 1 | 1 | 2 |
| ExpressionLexer.skipWhitespaces | 5 | 2 | 1 | 2 | 3 |
| Main.main | 6 | 0 | 1 | 1 | 1 |
| Polynomial.simplify | 18 | 8 | 5 | 5 | 5 |
| PolynomialParser.parse | 24 | 8 | 6 | 3 | 6 |
| PolynomialParser.parseFactor | 20 | 7 | 3 | 4 | 5 |
| PolynomialParser.parseInteger | 21 | 8 | 6 | 3 | 6 |
| PolynomialParser.parseTermFactors | 24 | 8 | 5 | 5 | 8 |
| SimplifiedPolynomial.differentiate | 15 | 3 | 3 | 2 | 3 |
| SimplifiedPolynomial.termToString | 32 | 11 | 2 | 6 | 7 |
| SimplifiedPolynomial.toString | 20 | 5 | 4 | 3 | 4 |
| tokens.MinusSign.getMultiplier | 4 | 0 | 1 | 1 | 1 |
| tokens.PlusSign.getMultiplier | 4 | 0 | 1 | 1 | 1 |
| 总计 | 230 | 78 | 46 | 47 | 63 |
| 平均值 | 16.43 | 5.57 | 3.29 | 3.36 | 4.5 |
这里略去了没有太大意义的构造器方法以及属性的 getter 和 setter 方法。从度量值中可以看出复杂度度量值偏高的主要是文法分析和语法分析的相关方法。其中文法分析方法ExpressionLexer.analyze由于需要多个条件分支判断不同的字符,加之实现时将部分本应由语法分析处理的功能放到了里面,导致各项度量值均较高;而PolynominalParser类中的语法分析相关方法本身逻辑就较为复杂,尽管本质圈复杂度偏高,但其余度量值正常,个人认为在可接受范围内。
类度量
| 类 | 代码行数 | 属性数 | 方法数 | 平均操作复杂度 | 最大操作复杂度 | 加权方法复杂度 | 循环依赖数 | 依赖数 | 被依赖数 |
|---|---|---|---|---|---|---|---|---|---|
| ConstantFactor | 9 | 1 | 0 | 1 | 1 | 2 | 0 | 1 | 2 |
| ExpressionLexer | 50 | 0 | 2 | 3.25 | 9 | 13 | 0 | 7 | 1 |
| Factor | 1 | 0 | 0 | N/A | N/A | 0 | 0 | 0 | 5 |
| Main | 8 | 0 | 1 | 1 | 1 | 1 | 0 | 5 | 0 |
| Polynomial | 24 | 0 | 1 | 3 | 5 | 6 | 0 | 5 | 2 |
| PolynomialParser | 96 | 0 | 4 | 4.6 | 6 | 23 | 0 | 11 | 1 |
| SimplifiedPolynomial | 73 | 0 | 3 | 3.75 | 7 | 15 | 0 | 0 | 2 |
| Term | 14 | 2 | 0 | 1 | 1 | 3 | 0 | 1 | 2 |
| VariableFactor | 9 | 1 | 0 | 1 | 1 | 2 | 0 | 1 | 2 |
| tokens.DoubleStarOperator | 1 | 0 | 0 | N/A | N/A | 0 | 0 | 1 | 2 |
| tokens.MinusSign | 6 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 |
| tokens.PlusSign | 6 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 |
| tokens.Sign | 3 | 0 | 0 | N/A | N/A | 0 | 0 | 1 | 3 |
| tokens.StarOperator | 1 | 0 | 0 | N/A | N/A | 0 | 0 | 1 | 2 |
| tokens.Token | 1 | 0 | 0 | N/A | N/A | 0 | 0 | 0 | 8 |
| tokens.UnsignedInteger | 9 | 1 | 0 | 1 | 1 | 2 | 0 | 1 | 2 |
| tokens.Variable | 1 | 0 | 0 | N/A | N/A | 0 | 0 | 1 | 2 |
| 总数 | 312 | 5 | 13 | 69 | |||||
| 平均值 | 18.35 | 0.29 | 0.76 | 1.96 | 3.09 | 4.06 | 0 | 2.24 | 2.24 |
复杂度相关度量的情况基本与方法度量的情况一致,即文法分析、语法分析以及字符串输出相关类的度量值偏高。SimplifiedPolynomial复杂度偏高主要是因为将整个表达式的求导和字符串输出功能都实现在了这个类里,如果再抽象出SimplifiedTerm类来处理单个项的求导和字符串输出的话应该可以降低复杂度。另外值得注意的是PolynomialParser类的依赖数明显偏高,这是因为我将实现文法分析时进行了部分本应放在语法分析环节的处理,导致部分标记需要携带不同的数据,就只好将不同的标记实现为不同的类。
类图
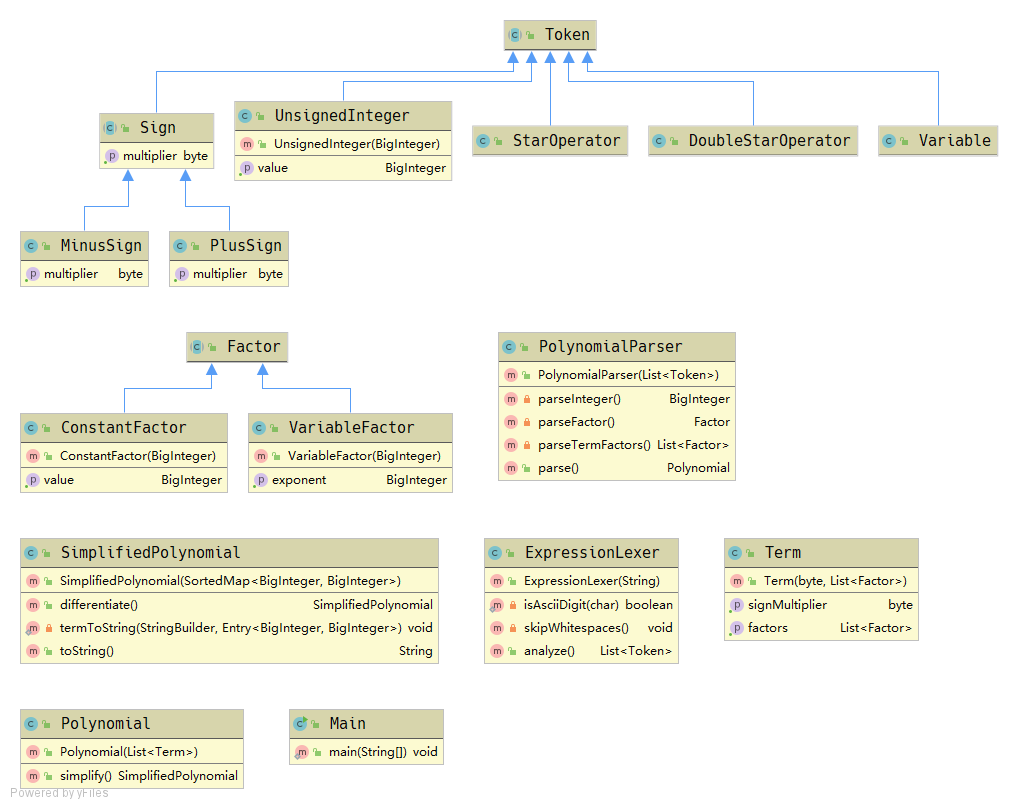
这次作业整体上分为两部分:表达式解析和表达式化简求导。
表达式解析的过程中首先由ExpressionLexer类对读取的字符传进行文法分析,将其转换为一串Token(标记)类,然后将它们传递给负责语法分析的PolynominalParser类,生成由Polynominal、Term、Factor等类组成的多项式。
多项式的语法结构分为Polynominal(多项式)、Term(项)、Factor(因子)三个层次,逐层包含;而因子又分为ConstantFactor(常量因子)和VariableFactor(幂函数因子)两种,分别包含对应的常量值和指数属性。Polynomial类提供的simplify方法可以将语法分析得到的多项式化简为统一的 \(\sum_ia_ix^{b_i}\) 的形式(其中 \(b_i\) 两两不同),并存储在SimplifidPolynomial类中,化简后的多项式就可以轻松地完成求导和字符串输出的操作。
第二次作业
方法度量
| 方法 | 代码行数 | 认知复杂度 | 本质圈复杂度 | 设计复杂度 | 圈复杂度 |
|---|---|---|---|---|---|
| ConstantFactor.differentiate | 4 | 0 | 1 | 1 | 1 |
| ConstantFactor.toString | 4 | 0 | 1 | 1 | 1 |
| Expression.SimplificationState.addTerm | 24 | 5 | 1 | 3 | 3 |
| Expression.differentiate | 7 | 1 | 1 | 2 | 2 |
| Expression.simplify | 33 | 12 | 5 | 7 | 8 |
| Expression.toString | 18 | 7 | 1 | 4 | 4 |
| ExpressionFactor.differentiate | 6 | 0 | 1 | 1 | 1 |
| ExpressionFactor.toString | 4 | 0 | 1 | 1 | 1 |
| Main.main | 6 | 0 | 1 | 1 | 1 |
| Parser.acceptSign | 19 | 7 | 6 | 4 | 6 |
| Parser.acceptToken | 9 | 1 | 2 | 1 | 2 |
| Parser.checkPos | 5 | 1 | 2 | 1 | 2 |
| Parser.checkToken | 4 | 0 | 1 | 1 | 1 |
| Parser.expectToken | 10 | 1 | 2 | 2 | 2 |
| Parser.parse | 6 | 0 | 1 | 1 | 1 |
| Parser.parseExpression | 13 | 4 | 3 | 2 | 4 |
| Parser.parseFactor | 26 | 9 | 6 | 6 | 7 |
| Parser.parseInteger | 5 | 1 | 1 | 2 | 2 |
| Parser.parseOptionalExponent | 7 | 2 | 2 | 2 | 2 |
| Parser.parseTerm | 14 | 3 | 1 | 4 | 4 |
| PowerFactor.differentiate | 7 | 0 | 1 | 1 | 1 |
| PowerFactor.toString | 4 | 1 | 1 | 2 | 2 |
| Term.SimplificationState.addFactor | 21 | 9 | 1 | 7 | 7 |
| Term.concat | 5 | 0 | 1 | 1 | 1 |
| Term.differentiate | 13 | 1 | 2 | 2 | 2 |
| Term.getExponents | 41 | 24 | 10 | 6 | 13 |
| Term.simplify | 36 | 15 | 4 | 9 | 9 |
| Term.toString | 17 | 4 | 3 | 4 | 4 |
| TermExponents.equals | 9 | 4 | 3 | 4 | 6 |
| TermExponents.hashCode | 4 | 0 | 1 | 1 | 1 |
| Token.getTokenString | 3 | 0 | 1 | 1 | 1 |
| Tokenizer.isAsciiDigit | 3 | 1 | 1 | 1 | 2 |
| Tokenizer.skipWhitespaces | 5 | 2 | 1 | 2 | 3 |
| Tokenizer.tokenize | 45 | 17 | 10 | 13 | 14 |
| TrigonometricFactor.differentiate | 19 | 3 | 3 | 3 | 3 |
| TrigonometricFactor.toString | 4 | 0 | 1 | 1 | 1 |
| VariableFactor.getExponentString | 3 | 1 | 1 | 1 | 2 |
| 总计 | 463 | 136 | 85 | 106 | 127 |
| 平均值 | 12.51 | 3.68 | 2.30 | 2.86 | 3.43 |
各项复杂度度量值明显偏高的方法有 3 个:
-
Term.getExponents方法的主要功能是检查当前项是否是简单的 \(ax^b\sin^c(x)\cos^d(x)\) 的形式,并获取这类项的各个指数以便表达式合并同类项。为了实现这个功能,该方法的逐个检查当前项的所有因子,大量使用instanceof关键字和复杂的嵌套条件语句,导致代码不够优雅,复杂度也过高。这个实现有较大的改进空间:可以将项分为复杂项和简单项两类,在执行项的化简时就处理好相关信息,并在可能时把复杂项转化为简单项,这样在合并同类项时就可以直接利用这些信息而无需重新进行不必要的复杂计算。 -
Tokenizer.tokenize负责文法分析,尽管它为了处理各种不同字符而包含了一个较长的 if-else 语句导致复杂度度量值很高,但是个人认为这样的实现实际阅读起来并不困难,逻辑也很清晰,没有太大的改进空间。 -
Term.simplify方法度量值偏高,原因主要是为了方便将一些本应由ExpressionFactor类(表达式因子)处理的化简逻辑放在了这个方法里;事实上Expression.simplify方法也有类似的问题,只是并没有在度量值中体现出来。这个问题在之后的第三次作业中得到了改善。
类度量
| 类 | 代码行数 | 属性数 | 方法数 | 平均操作复杂度 | 最大操作复杂度 | 加权方法复杂度 | 循环依赖数 | 依赖数 | 被依赖数 |
|---|---|---|---|---|---|---|---|---|---|
| ConstantFactor | 17 | 1 | 2 | 1 | 1 | 4 | 9 | 2 | 7 |
| Expression | 67 | 1 | 3 | 3 | 7 | 15 | 9 | 5 | 4 |
| Expression.SimplificationState | 29 | 0 | 1 | 3 | 3 | 3 | 9 | 4 | 1 |
| ExpressionFactor | 19 | 1 | 2 | 1 | 1 | 4 | 9 | 3 | 4 |
| Factor | 3 | 0 | 1 | N/A | N/A | 0 | 9 | 1 | 8 |
| Main | 8 | 0 | 1 | 1 | 1 | 1 | 0 | 4 | 0 |
| Parser | 125 | 0 | 11 | 2.75 | 6 | 33 | 0 | 10 | 1 |
| PowerFactor | 16 | 0 | 2 | 1.33 | 2 | 4 | 9 | 3 | 3 |
| Term | 121 | 1 | 5 | 4.14 | 13 | 29 | 9 | 10 | 8 |
| Term.SimplificationState | 28 | 0 | 1 | 7 | 7 | 7 | 9 | 7 | 1 |
| TermExponents | 27 | 0 | 2 | 1.67 | 3 | 5 | 0 | 0 | 2 |
| Token | 24 | 4 | 0 | 1 | 1 | 5 | 0 | 1 | 3 |
| TokenType | 3 | 0 | 0 | N/A | N/A | 0 | 0 | 0 | 3 |
| Tokenizer | 61 | 0 | 3 | 3.75 | 11 | 15 | 0 | 2 | 1 |
| TrigonometricFactor | 33 | 1 | 2 | 1.5 | 3 | 6 | 9 | 4 | 3 |
| TrigonometricFunction | 3 | 0 | 0 | N/A | N/A | 0 | 0 | 0 | 4 |
| VariableFactor | 12 | 1 | 1 | 1.33 | 2 | 4 | 9 | 1 | 4 |
| 总计 | 596 | 10 | 37 | 135 | |||||
| 平均值 | 35.06 | 0.59 | 2.18 | 2.39 | 4.36 | 7.94 | 5.29 | 3.35 | 3.35 |
Term类和Tokenizer类复杂度过高的问题在方法度量部分已有说明。Term.SimplificationState类尽管平均操作复杂度看起来很高,但这是因为它仅包含一个复杂度略微偏高的方法,它的存在仅仅是为了规避 Java 的 lambda 表达式不能修改捕获的变量的限制,在逻辑上应该算作Term类的一部分,因此没有必要对这个过高的平均值过于关注。
值得注意的是尽管负责语法分析的Parser类的各个方法的度量值都不算很高,但是由于它包含的方法数较多,导致整个类的加权方法复杂度很高,可以考虑将其拆分成分别负责解析表达式不同部分的多个类。
循环依赖的出现是由于这次作业的要求增加了表达式因子,所以新增的ExpressionFactor依赖了Expression。Parser类和Tokenizer类由于需要处理Factor类的各个子类,依赖数较高。
类图
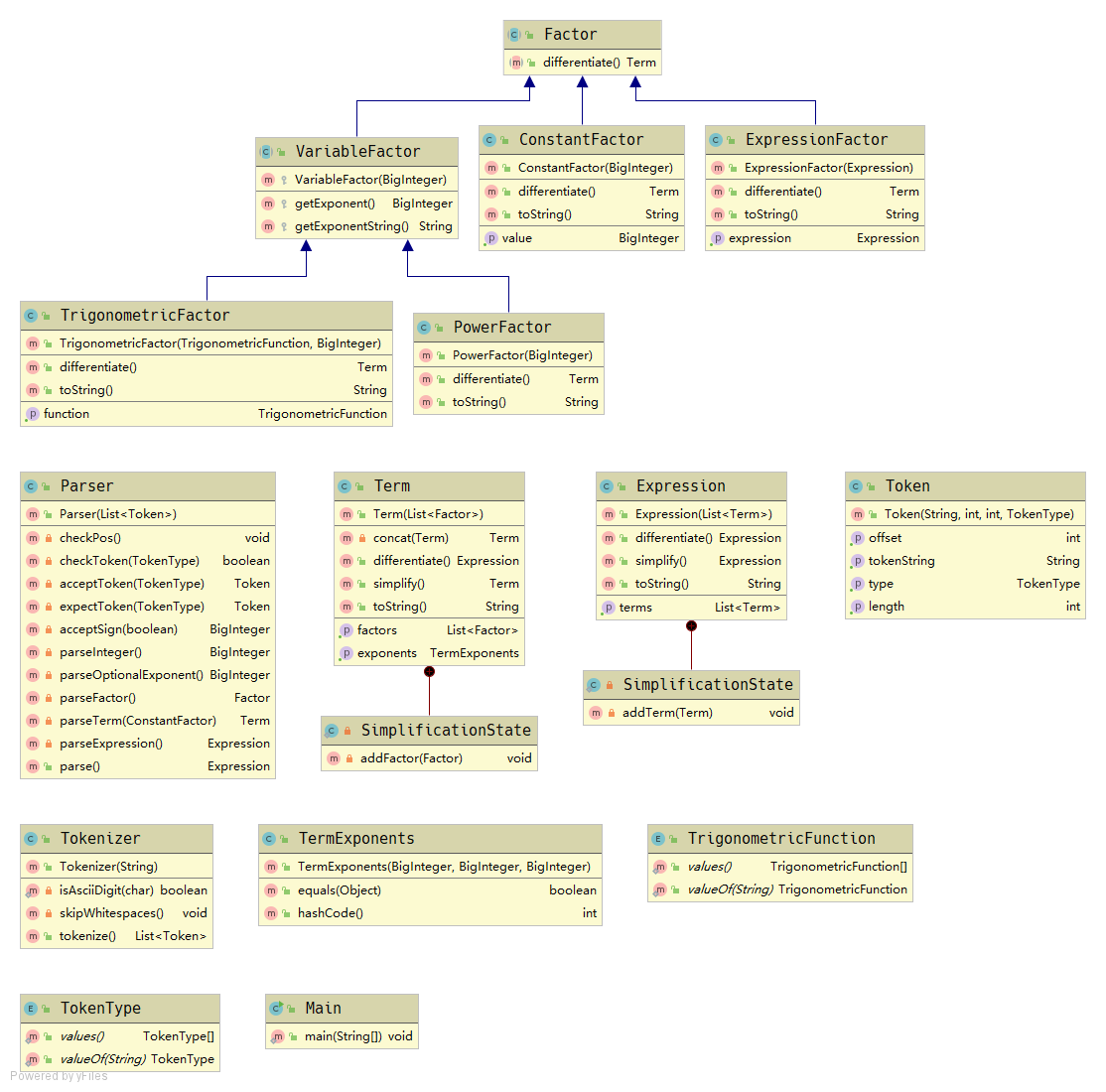
表达式解析部分相比第一次作业没有太大的变化,仍然是使用了一个负责文法分析的Tokenizer类和一个负责语法分析的Parser类,不过这次不再使用类来表示文法分析结果中的不同的标记,而是全部使用一个Token类,其中记录了标记类型以及它在输入字符串中的位置以供语法分析时使用。
表达式树的结构大致与第一次作业相同,只是增加了ExpressionFactor类,并将VariableFactor类拆分成TrigonometricFactor和PowerFactor两个子类,用于支持新增的表达式因子和三角函数因子。另外考虑到输入不再是多项式了,将Polynomial类改名成了Expression类。
化简和求导的处理则是做了较大的改变,不再使用原来的先化简成特定形式在求导的方法,而是直接在表达式树上进行求导并化简,最后得到的结果仍是Expression类,然后再在表达式树上实现toString方法完成字符串输出。
第三次作业
第三次作业的代码是在第二次作业的基础上进行简单的修改得到的,因此下面仅列出有改动的方法和类的度量值。
方法度量
| 方法 | 代码行数 | 认知复杂度 | 本质圈复杂度 | 设计复杂度 | 圈复杂度 |
|---|---|---|---|---|---|
| ConstantFactor.simplify | 4 | 0 | 1 | 1 | 1 |
| Expression.SimplificationState.addTerm | 24 | 10 | 2 | 4 | 4 |
| Expression.isZero | 5 | 1 | 2 | 1 | 2 |
| Expression.simplify | 31 | 10 | 4 | 6 | 7 |
| Expression.tryExtractFactor | 5 | 1 | 2 | 1 | 2 |
| Expression.tryExtractTerm | 4 | 1 | 2 | 1 | 2 |
| ExpressionFactor.simplify | 4 | 0 | 1 | 1 | 1 |
| Factor.toStringNoExpand | 3 | 0 | 1 | 1 | 1 |
| Main.main | 13 | 1 | 1 | 2 | 2 |
| Parser.parseFactor | 26 | 10 | 6 | 6 | 7 |
| Parser.parseOptionalExponent | 11 | 5 | 3 | 3 | 4 |
| PowerFactor.simplify | 4 | 0 | 1 | 1 | 1 |
| PowerFactor.toStringNoExpand | 4 | 0 | 1 | 1 | 1 |
| Term.SimplificationState.addFactor | 9 | 3 | 1 | 3 | 3 |
| Term.getSimpleInfo | 26 | 13 | 6 | 4 | 8 |
| Term.isZero | 6 | 2 | 2 | 2 | 3 |
| Term.simplify | 29 | 11 | 4 | 7 | 7 |
| Term.tryExtractExpression | 9 | 3 | 3 | 2 | 3 |
| Term.tryExtractFactor | 4 | 1 | 2 | 1 | 2 |
| TrigonometricFactor.differentiate | 34 | 3 | 3 | 3 | 3 |
| TrigonometricFactor.simplify | 33 | 19 | 8 | 8 | 10 |
| TrigonometricFactor.toString | 9 | 0 | 1 | 1 | 1 |
Term.getSimpleInfo是由第二次作业中的Term.getExponents重命名并修改而来的,去除了带三角函数的项的合并同类项,复杂度有所降低。但由于实现方法仍然是暴力地扫描所有因子进行判断,复杂度还是偏高。Term.simplify和Expression.simplify因为去除了三角函数的指数合并,并将去括号的逻辑提取到了新的方法中,复杂度得到了控制。TrigonometricFactor.simplify因为同时处理了 \(\sin\) 和 \(\cos\) 两种三角函数并且包含了特殊值的优化,导致代码过于复杂,可以考虑将两种三角函数分别实现为TrigonometricFactor的两个子类,并将特殊值的判断提取的到单独的方法中。
类度量
| 类 | 代码行数 | 属性数 | 方法数 | 平均操作复杂度 | 最大操作复杂度 | 加权方法复杂度 | 循环依赖数 | 依赖数 | 被依赖数 |
|---|---|---|---|---|---|---|---|---|---|
| ConstantFactor | 21 | 1 | 3 | 1 | 1 | 5 | 8 | 2 | 7 |
| Expression | 79 | 1 | 6 | 2.5 | 6 | 20 | 8 | 4 | 5 |
| Expression.SimplificationState | 29 | 0 | 1 | 4 | 4 | 4 | 8 | 4 | 1 |
| ExpressionFactor | 23 | 1 | 3 | 1 | 1 | 5 | 8 | 3 | 3 |
| Factor | 7 | 0 | 3 | 1 | 1 | 1 | 8 | 1 | 10 |
| Main | 15 | 0 | 1 | 1 | 1 | 1 | 0 | 5 | 0 |
| Parser | 131 | 0 | 11 | 2.83 | 6 | 34 | 0 | 11 | 1 |
| PowerFactor | 24 | 0 | 4 | 1.2 | 2 | 6 | 8 | 4 | 3 |
| SimpleTermInfo | 14 | 2 | 0 | 1 | 1 | 3 | 0 | 0 | 2 |
| Term | 118 | 1 | 8 | 2.9 | 8 | 29 | 8 | 8 | 8 |
| Term.SimplificationState | 14 | 0 | 1 | 3 | 3 | 3 | 8 | 4 | 1 |
| TrigonometricFactor | 89 | 0 | 3 | 3.5 | 9 | 14 | 0 | 7 | 1 |
| WrongFormatException | 5 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 3 |
Term.SimplificationState因为去除了三角函数的处理复杂度明显降低。TrigonometricFactor的simplify方法复杂度过高导致其平均复杂度也偏高。Parser因为增加了指数范围限制的相关代码,复杂度再次提高,确实有必要对其进行拆分。
类图
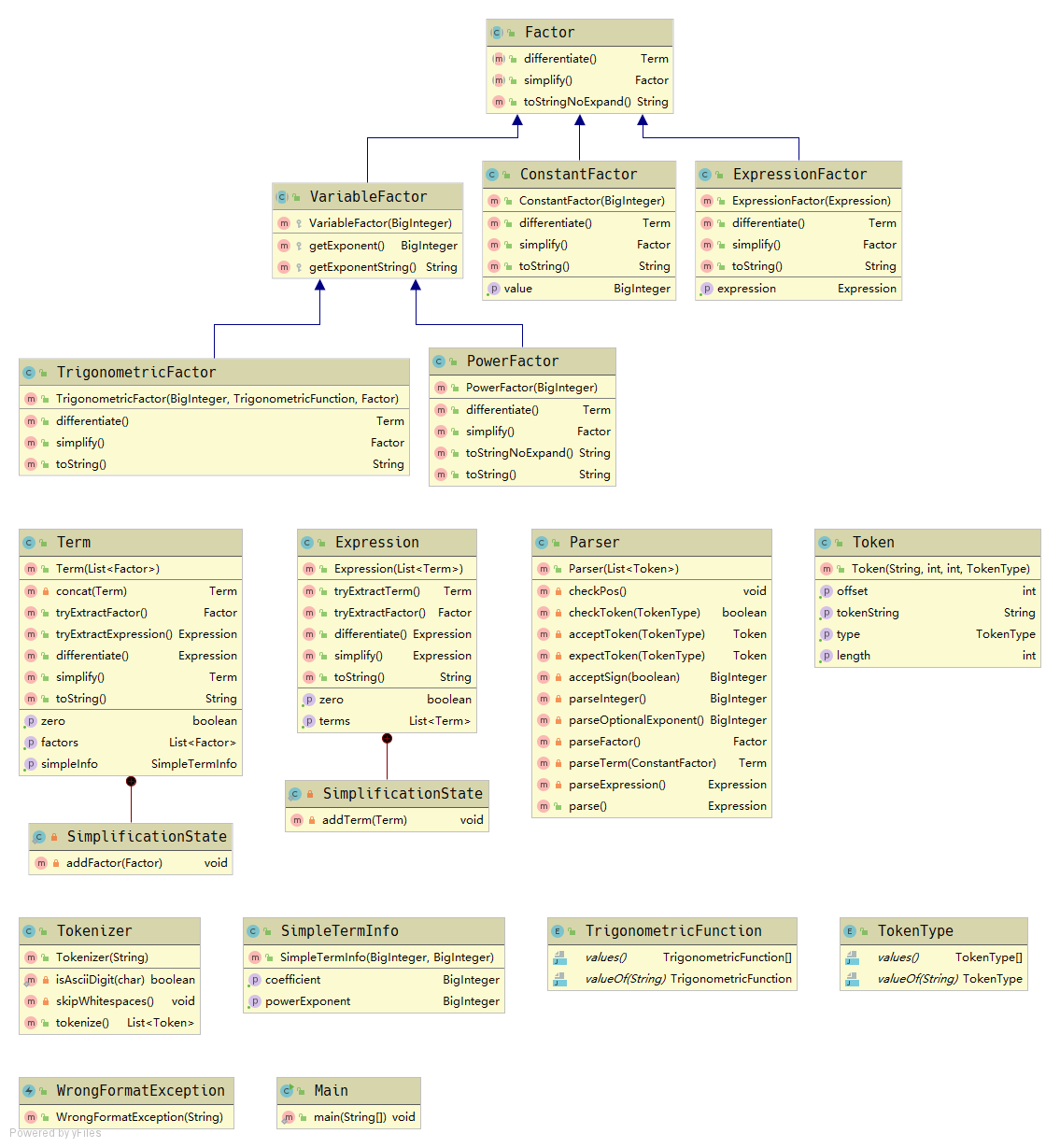
第三次作业的架构与第二次作业基本一致,只做了少量的更改:
TermExponents改为SimpleTermInfo,去掉了三角函数指数的支持。- 将拆括号的逻辑从
simplify方法提取到了几个extractXxx方法中。 - 将原来在
Term.simplify方法中处理的一些化简逻辑提取到了Factor类及其子类的simplify方法中。 - 新增
WrongFormatException以便处理表达式解析错误并按题目要求输出错误信息。
bug 分析
第一次作业
第一次作业中出现的 bug 是空白字符处理的问题。由于ExpressionLexer.analyze方法中读取字符的循环中跳过空白字符和结束退出的逻辑有问题,导致当输入的表达式末尾有空白字符时程序会误认为表达式格式错误而抛出异常。相关代码如下:
index = 0;
// other initialization
while (index < data.length()) {
skipWhitespaces();
final char c = data.charAt(index);
index++;
// process input
}
当遇到表达式末尾前的空格时,由于index变量还未到达字符串结束处,会再次进入循环,执行skipWhitespaces()跳过空白字符后,index变量抵达字符串末尾,这是程序再尝试读取新的字符,就导致了IndexOutOfBoundsException异常。
在自己测试时没有发现这个 bug 是因为编写测试程序时只关注了化简和求导的正确性,生成的数据没有在其中加入空格。由于公测数据较弱,这个 bug 在公测时没有导致任何问题,但是在互测阶段却被多达十组数据 hack,其中大多数甚至都不是针对我的。
出现错误代码的ExpressionLexer.analyze方法的代码行数和圈复杂度等各项度量值在这次作业的所有方法中都是最高的,这也印证了复杂的方法确实容易出现 bug。
第二次作业
第二次作业在公测和互测阶段都没有发现任何 bug。
第三次作业
第三次作业遇到了两个 bug:
-
在最后字符串输出时,
PowerFactor.toString方法会把因子 \(x^2\) 以x*x的形式输出以缩短长度,而在TrigonometricFactor.toString方法中直接使用因子的toString方法,导致产生了sin(x*x)和cos(x*x)的错误输出。public class PowerFactor extends VariableFactor { // other members @Override public String toString() { return getExponent().equals(BigInteger.valueOf(2)) ? "x*x" : "x" + getExponentString(); } } public class TrigonometricFactor extends VariableFactor { // other members @Override public String toString() { return String.format( "%s(%s)%s", function.name().toLowerCase(Locale.ROOT), factor, getExponentString() ); } }这个优化会导致输出从一个因子变成两个因子组成的项,因此就要求输出幂函数因子的地方能够使用这两种形式。我是在第二次作业时添加这个优化的,当时三角函数的自变量只可能是单独的一个
x,幂函数因子只可能作为项的一部分出现,因此输出x*x一定是合法的。但第三次作业允许三角函数的自变量为任意因子,这就使得上述要求不一定满足,而我没有注意到原来的代码存在这个问题,导致了这个 bug 的出现。在自己测试时,我的测试程序忘记考虑了输出可能不合法的问题,没有对程序输出格式进行验证,而是直接将其传递给 SymPy 进行处理,这就导致这种不符合作业要求但能被 SymPy 解析的输出无法被检测出来。这个 bug 导致我的这次作业在公测和互测时均有多个数据点出错。
与这个 bug 相关的两个
toString函数的代码行数等度量值都很低,复杂度并不是出现 bug 的诱因。但是在分析 bug 时可以发现,PowerFactor.toString的实现过于依赖其原先的调用方式了,只有被允许项形式的返回值的调用方(如Term.toString)调用时,其返回值才能保证是合法的,因此在有新的不同的调用方时就不适用了,也就是说原先的代码存在着过度耦合的问题。或者从另一个角度来看,toString方法应该返回的是它所在类的字符串表示,对于这里的情况就应该是一个因子的字符串表示,而现在其实现却可能返回一个项的字符串表示,这种预期与实际的差异导致编写调用它的代码时出现了问题。 -
第二个 bug 相对来说严重性低一些。在化简三角函数时,程序只化简了
sin((0))和cos((0))这样常量嵌套在表达式内的情况,但没有化简sin(0)和cos(0)这样常量因子直接作为参数的情况。这是因为在刚开始编写第三次作业时,我看错了题目要求,误以为三角函数的参数是一个表达式,因此相关代码都是以嵌套着表达式为前提编写的;而在发现题目实际上要求三角函数的参数是因子后,我在修改原来的错误代码时就忘记考虑常量因子的情况了。这种程序没有按预期工作的情况我认为也应该被视为一个 bug,不过它并没有导致程序产生不合法的输出,只是在部分情况下导致了性能降低,在作业中也只是对性能分产生了很小的影响。
包含错误代码的
TrigonometricFactor.simplify方法的各项度量值都明显偏高,排名均在前三,其中认知复杂度甚至是所有方法中最高的。应该认为该方法过高的复杂度与 bug 的出现有关联。
发现他人 bug 的策略
本次作业的互测环节我采用的是自动化测试为主,人工阅读代码为辅的策略。在互测开始后,我一般首先使用先前测试自己代码时就编写好的自动测试程序随机生成输入数据对房间内所有同学的程序进行模糊测试,在发现有问题的程序后,再仔细阅读该同学的代码,找出出现 bug 的原因并构造测试数据用于提交。
这个方法的优点有:
- 完整阅读房间内所有同学的代码工作量极大,在有限的互测时间内很难完成,而首先进行自动化测试可以筛选掉一些不太可能有 bug 的程序,提高效率。根据这几次作业的经验,一个房间内有 bug 的代码一般为 3 份左右,也就是说自动化测试可以减少大约 50% 的代码阅读量。
- 直接阅读代码并不能保证一定能发现代码中的 bug ,而利用自动化测试发现的测试数据可以有针对性地检查代码或进行调试,帮助在阅读代码的过程中快速定位 bug。
- 在测试他人代码时对测试程序的改进也有助于发现自己程序的 bug。
- 自动化的模糊测试仅能确认 bug 的存在,但不能定位 bug 的原因,也不能区分不同测试数据复现的是否是同一个 bug,只有在阅读代码以后才能精确地定位 bug,避免无意义地提交针对同一个 bug 的不同测试数据,在提交次数有限的情况下尽量覆盖同一份代码里的多个不同 bug。
- 在阅读他人代码的过程,可以学习其方法和技巧,并以其中存在的问题警示自己。
事实证明这个策略是十分有效的,从 hack 记录来看,在三次作业的互测阶段我都基本找出了房内所有的 bug。
重构经历总结
我在实现第二次作业时对第一次作业的代码进行了较大规模的重构(不如说是重写),而在实现第三次作业时仅对第二次作业的代码进行了较小的改动。
这是因为第三次作业的要求相对于第二次作业改变不是很大,识别输入格式错误的功能在前两次作业中已经顺便实现,而三角函数支持嵌套因子也可以在已有的框架下完成。
相比之下,第二次作业的要求就很难在我第一次作业的框架下实现:
- 第二次作业的输入表达式相对较为复杂,存在递归嵌套的情况,所以原来随便写的语法分析类需要以递归下降的方式重写。
- 在第一次作业中,作为词法分析结果的标记时使用类继承的层次结构实现的,这产生了大量只有两三行的不必要的类,所以要改为只使用一个类和枚举类型来实现,相应地词法分析类也需要不小的改动。
- 第一次作业采用了先化简为一般形式再求导的方法,但是第二次作业涉及嵌套的表达式,若全部展开不但麻烦还可能导致结果过长,所以求导和化简需要直接在解析得到的表达式树上执行,相关代码需要全部重写。
除了表达式树的大致结构得到保留以外,几乎所有代码都进行了重写。不过我认为这并不应该归咎于第一次作业时设计不当。在不知道可能的扩展方向的情况下(我不认为通过了解往届作业来提前得知之后作业的需求是什么好的做法),采用我第一次作业中使用的设计是十分自然的做法。相反,如果一味地追求可扩展性,用过于复杂的架构来实现简单的需求,导致开发效率降低,在我看来才是得不偿失的做法。
心得体会
我之前就使用过 C# 等面向对象的语言,对于面向对象语言中常见的概念都比较熟悉,不过因为以前没怎么用 Java 写过程序,所以在这单元的作业中更多地是熟悉了 Java 的基本语法和标准类库。此外,由于作业涉及到表达式字符串的解析,还意外地了解到了属于编译领域的递归下降算法等知识。
尽管化简表达式的需求看起来比较恐怖,但是实际上性能分的给分相当友善,所占比例也不高,只要不是特别离谱感觉就能得到相当高的强测成绩。这几次作业我都只实现了非常简单的化简,最后性能分导致的扣分都在 1 分以内。
相比之下如果程序中有 bug 导致公测有测试点没过,会被扣掉相当多的分数,比如第三次作业中我就有两个测试点没过而丢了 10 分。比较有趣的一点是这单元中我提交的代码中的所有 bug 都不是在互测结束数据公布后才发现的,而是在互测时为了发现别人代码中的 bug 而改进自动测试程序时发现的。也就是说如果能够更全面地测试自己的代码的话,这些 bug 本来是能在提交前就被发现并修复,而不至于失分的,有必要引起重视。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号