18. 二叉树和二叉搜索树的最近公共祖先

📃 题目一描述

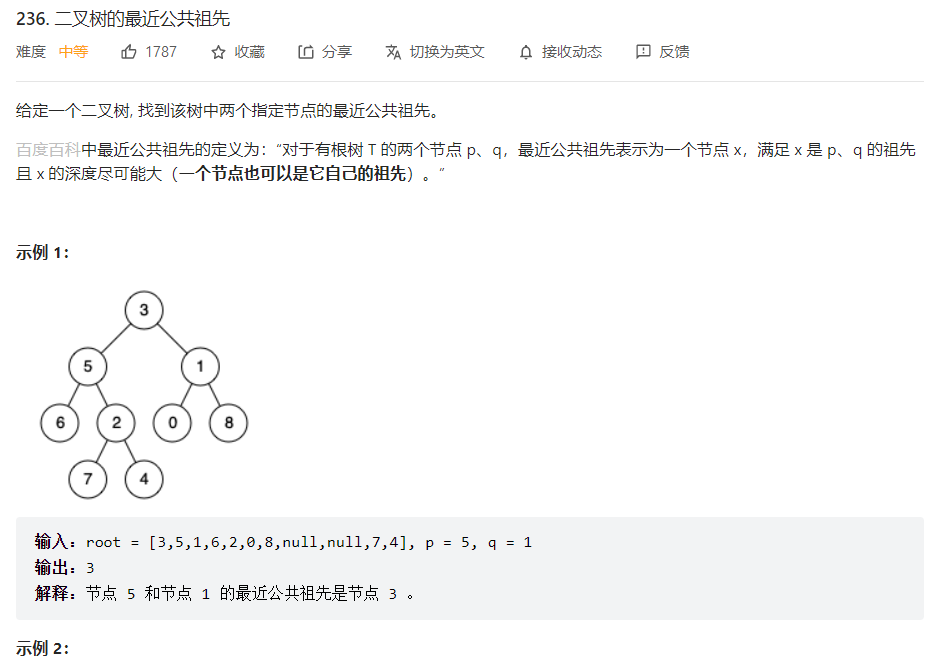
题目链接：236. 二叉树的最近公共祖先

🔔 解题思路

1. 思考两个节点散布在二叉树上，应该是回溯 自底向上 遍历，才会得到结果；

2. 要明白有一种情况是：必有也仅存在这样一个节点，左子树中含有一个要查询的节点，右子树中含有另一个要查询的节点；其他节点都是要么不包含，要么只在一个子树中包含；

3. 另一种情况是：p或者q本身就是最近公共祖先；即答案是p或者q；

   所以我们采用遇到p或q节点就返回，无需继续遍历；（我们可以假设答案就是第二种情况，那么遇到p或者q就返回，但是如果继续向上遍历过程中，遇到第2点的情况，那么这个就是答案；）

class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        if (root == p || root == q || !root) return root; // 两种情况都考虑了
        // 后序遍历
        TreeNode* left = lowestCommonAncestor(root->left, p, q);
        TreeNode* right = lowestCommonAncestor(root->right, p, q);
        
        if (left && right) return root; // 是公共祖先
        else if (!left && right) return right; // 子树中存有一个子节点
        else if (!right && left) return left; // 子树中存有一个子节点
        else return nullptr;
    }
};

💥 复杂度分析

• 时间复杂度：O(n);
• 空间复杂度：O(n);

📃 题目二描述

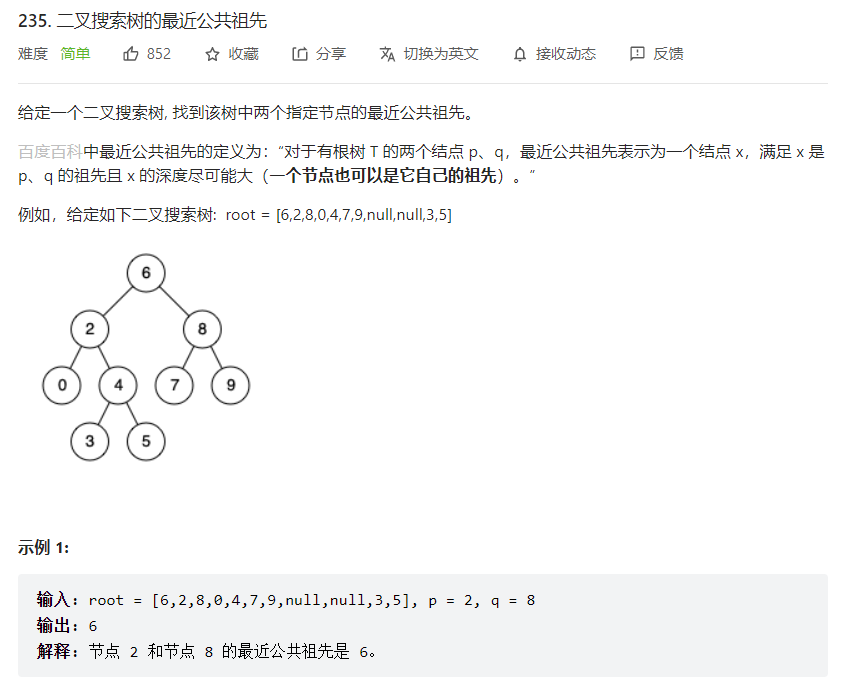
题目链接：235. 二叉搜索树的最近公共祖先

🔔 解题思路

这道题也可以用上面的解法处理；

但是明显我们还可以用到BST树的性质；思路：

BST树中左子树都小于root->val，右子树都大于root->val，所以可以采用这种特效，看看能否减少一条边的查询！

• 如果能，即答案在root节点的某一个子树上；
• 而如果不能，证明左子树含有一个节点，右子树含有一个节点，那么该节点就是答案；

class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        if (root == p || root == q || root == nullptr) return root; // 可以省略，因为最后必有答案；

        if (root->val > p->val && root->val > q->val) {
            return lowestCommonAncestor(root->left, p, q);
        }
        else if (root->val < p->val && root->val < q->val) {
            return lowestCommonAncestor(root->right, p, q);
        }
        else return root; // p、q节点在该节点左右两边，这个节点必是公共祖先
    }
};

遍历法：

class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        while (root) {
            if (root->val > p->val && root->val > q->val) { // 所找节点在左子树
                root = root->left;
            }
            else if (root->val < p->val && root->val < q->val) { // 所找节点在右子树
                root = root->right;
            }
            else break; // 左右子树都存在所找的节点；
        }
        return root;
    }
};

💥 复杂度分析

• 时间复杂度：O(n);
• 空间复杂度：O(1);