JZ013:二维子矩阵的和
📃 题目描述
题目链接:二维子矩阵的和
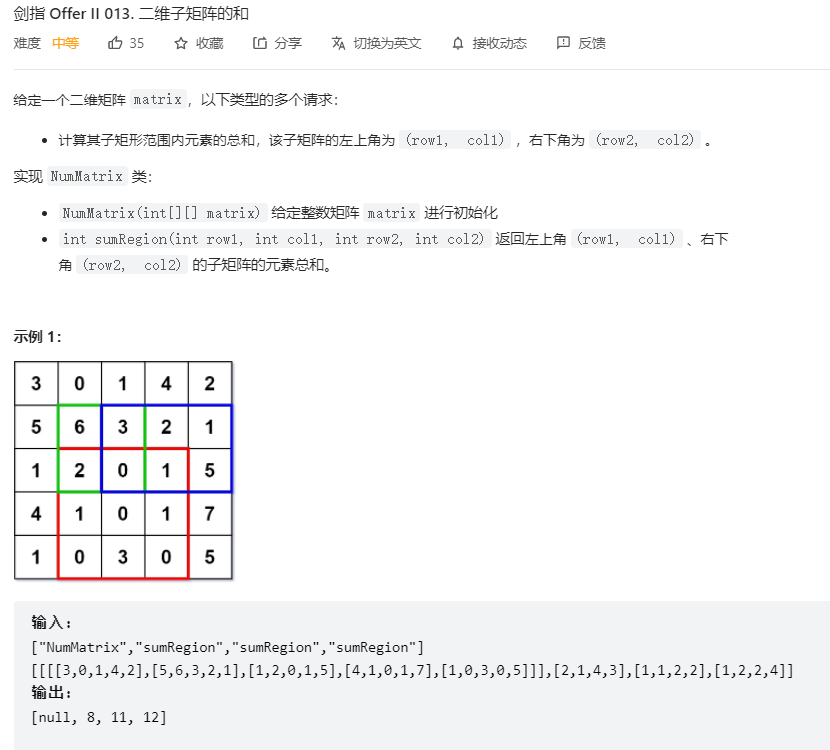
🔔 解题思路
二维数组前缀和模板题,最主要的问题就是边界问题,最好的解决方案:
加多两个边界:
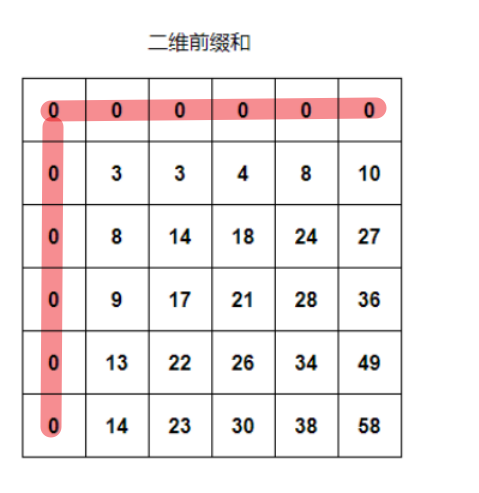
class NumMatrix {
public:
vector<vector<int>> sum;
NumMatrix(vector<vector<int>>& matrix) {
sum = vector<vector<int>> (matrix.size() + 1, vector<int>(matrix[0].size() + 1, 0));//处理边界问题,加多两条边界, 全部初始化为0;matrix[0][0] => sum[1][1];
//初始化中间
for (int i = 1; i <= matrix.size(); i++) {
for (int j = 1; j <= matrix[0].size(); j++) {
sum[i][j] = sum[i - 1][j] + sum[i][j - 1] - sum[i - 1][j - 1] + matrix[i - 1][j - 1];
}
}
}
int sumRegion(int row1, int col1, int row2, int col2) {
int res = sum[row2 + 1][col2 + 1];
res = res - sum[row2 + 1][col1] - sum[row1][col2 + 1];
res += sum[row1][col1];
return res;
}
};
💥 复杂度分析
- 时间复杂度:构建o(n *m), 求值o(1);
- 空间复杂度:O(n * m)


 浙公网安备 33010602011771号
浙公网安备 33010602011771号