1.77组合

📃 题目描述

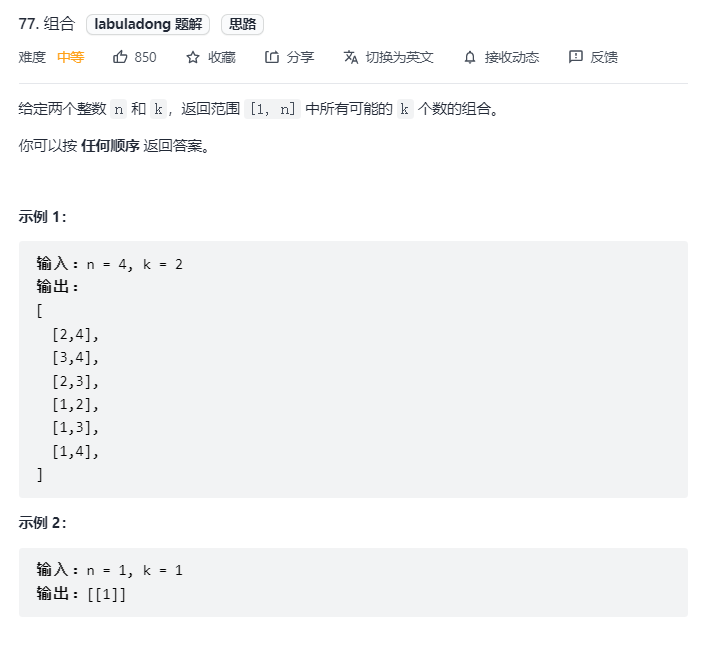
题目链接：组合问题

🔔 解题思路

采用暴力解法，回溯法用递归来解决嵌套层数的问题，得到的子结果都是升的，即从小到大遍历就行，如代码：int i = startIndex, 因为135和531是一样的；

将结果保存再res中； 将子结果保存在path中；

1.确定回溯函数返回值和参数：返回值为void，参数有取数最大值n，和要取的个数k，起始点startIndex；

2.终止条件：当path.size() == k的时候就压入res中，并且返回；

3.每一层遍历：从startIndex开始遍历， 遍历到9，将数字压入path中，进入递归， 然后出来递归后弹出；

vector<vector<int>> res;
vector<int> path;
vector<vector<int>> combine(int n, int k) {
    if (n < k) return {{}};//找实际数据模拟
    backTracking(n, k, 1);
    return res;
}
void backTracking(int n, int k, int startIndex) {
    if (path.size() == k){
        res.push_back(path);
        return;
    }
    for (int i = startIndex; i <= n; i++) {
        path.push_back(i);
        backTracking(n, k, i + 1);
        path.pop_back();
    }
}

剪支：

1.递归深度，递归结束条件是path里面一共有k个元素，并没有其他隐性条件，所以无法优化；

2.每一层的遍历，如果for循环选择的起始位置之后的元素个数 已经不足 我们需要的元素个数了，那么就没有必要搜索了， 如图：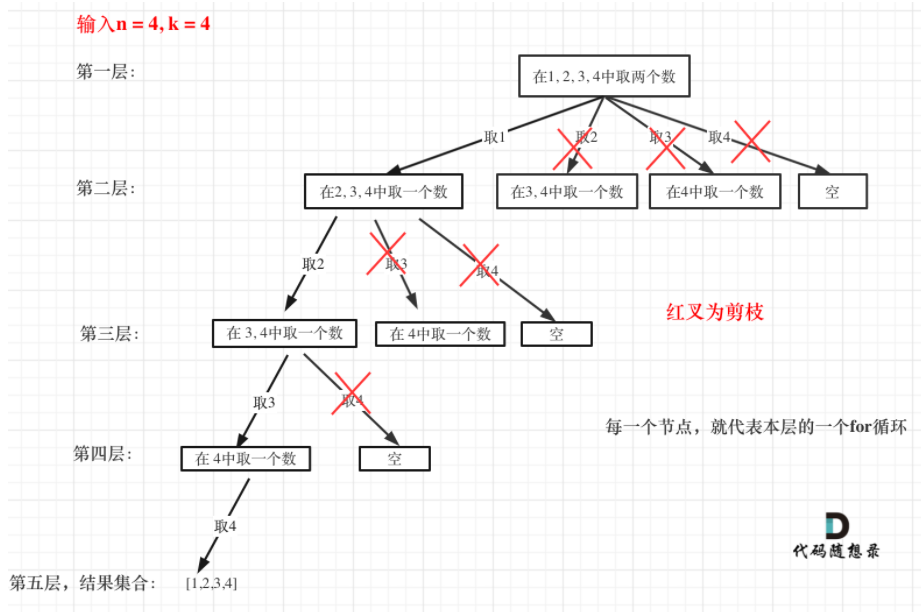

所以可以减少遍历的数量，k - path.size()为还需要的元素个数，n - (k - path.size()) + 1 为可以遍历到的最大数的位置；

所以可以优化：

for (int i = startIndex; i <= n - (k - path.size()) + 1; i++)

💥 复杂度分析

• 空间复杂度：o()
• 时间复杂度：O()