数据标准化处理-特征缩放（Feature Scaling）

数据的标准化（normalization）和归一化

数据的标准化（normalization）是将数据按比例缩放，使之落入一个小的特定区间。在某些比较和评价的指标处理中经常会用到，去除数据的单位限制，将其转化为无量纲的纯数值，便于不同单位或量级的指标能够进行比较和加权。其中最典型的就是数据的归一化处理，即将数据统一映射到[0,1]区间上。

    目前数据标准化方法有多种，归结起来可以分为直线型方法(如极值法、标准差法)、折线型方法(如三折线法)、曲线型方法(如半正态性分布)。不同的标准化方法，对系统的评价结果会产生不同的影响，然而不幸的是，在数据标准化方法的选择上，还没有通用的法则可以遵循。

归一化的目标

1 把数变为（0，1）之间的小数
        主要是为了数据处理方便提出来的，把数据映射到0～1范围之内处理，更加便捷快速，应该归到数字信号处理范畴之内。
2 把有量纲表达式变为无量纲表达式
        归一化是一种简化计算的方式，即将有量纲的表达式，经过变换，化为无量纲的表达式，成为纯量。 比如，复数阻抗可以归一化书写：Z = R + jωL = R(1 + jωL/R) ，复数部分变成了纯数量了，没有量纲。
另外，微波之中也就是电路分析、信号系统、电磁波传输等，有很多运算都可以如此处理，既保证了运算的便捷，又能凸现出物理量的本质含义。

特征缩放的几种方法：

（1）最大最小值归一化（min-max normalization）：将数值范围缩放到 [0, 1] 区间里

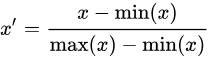
（2）均值归一化（mean normalization）：将数值范围缩放到 [-1, 1] 区间里，且数据的均值变为0

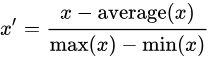
（3）标准化 / z值归一化（standardization / z-score normalization）：将数值缩放到0附近，且数据的分布变为均值为0，标准差为1的标准正态分布（先减去均值来对特征进行 中心化 mean centering 处理，再除以标准差进行缩放）

（4）最大绝对值归一化（max abs normalization ）：也就是将数值变为单位长度（scaling to unit length），将数值范围缩放到 [-1, 1] 区间里

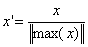
（5）稳键归一化（robust normalization）：先减去中位数，再除以四分位间距（interquartile range），因为不涉及极值，因此在数据里有异常值的情况下表现比较稳健

* 有一些时候，只对数据进行中心化和缩放是不够的，还需对数据进行白化（whitening）处理来消除特征间的线性相关性。

归一化和标准化的区别：

归一化（normalization）：归一化是将样本的特征值转换到同一量纲下，把数据映射到[0,1]或者[-1, 1]区间内。

标准化（standardization）：标准化是将样本的特征值转换为标准值（z值），每个样本点都对标准化产生影响。

为什么要进行特征缩放？

1. 统一特征的权重&提升模型准确性

如果某个特征的取值范围比其他特征大很多，那么数值计算（比如说计算欧式距离）就受该特征的主要支配。但实际上并不一定是这个特征最重要，通常需要把每个特征看成同等重要。归一化/标准化数据可以使不同维度的特征放在一起进行比较，可以大大提高模型的准确性。

2. 提升梯度下降法的收敛速度

在使用梯度下降法求解最优化问题时， 归一化/标准化数据后可以加快梯度下降的求解速度。

具体使用哪种方法进行特征缩放？

在需要使用距离来度量相似性的算法中，或者使用PCA技术进行降维的时候，通常使用标准化（standardization）或均值归一化（mean normalization）比较好，但如果数据分布不是正态分布或者标准差非常小，以及需要把数据固定在 [0, 1] 范围内，那么使用最大最小值归一化（min-max normalization）比较好（min-max 常用于归一化图像的灰度值）。但是min-max比较容易受异常值的影响，如果数据集包含较多的异常值，可以考虑使用稳键归一化（robust normalization）。对于已经中心化的数据或稀疏数据的缩放，比较推荐使用最大绝对值归一化（max abs normalization ），因为它会保住数据中的０元素，不会破坏数据的稀疏性（sparsity）。

哪些机器学习模型必须进行特征缩放？

通过梯度下降法求解的模型需要进行特征缩放，这包括线性回归（Linear Regression）、逻辑回归（Logistic Regression）、感知机（Perceptron）、支持向量机（SVM）、神经网络（Neural Network）等模型。此外，近邻法（KNN），K均值聚类（K-Means）等需要根据数据间的距离来划分数据的算法也需要进行特征缩放。主成分分析（PCA），线性判别分析（LDA）等需要计算特征的方差的算法也会受到特征缩放的影响。

决策树（Decision Tree），随机森林（Random Forest）等基于树的模型不需要进行特征缩放，因为特征缩放不会改变样本在特征上的信息增益。

进行特征缩放的注意事项：

需要先把数据拆分成训练集与验证集，在训练集上计算出需要的数值（如均值和标准值），对训练集数据做标准化/归一化处理（不要在整个数据集上做标准化/归一化处理，因为这样会将验证集的信息带入到训练集中，这是一个非常容易犯的错误），然后再用之前计算出的数据（如均值和标准值）对验证集数据做相同的标准化/归一化处理。

3、特征缩放的解释

进行缩放后，多维特征将具有相近的尺度，这将帮助梯度下降算法更快地收敛。 为了解释为什么特征缩放会帮助梯度下降算法更快地收敛，Andrew给了两幅图来解释：

Feature Scaling

Idea: Make sure features are on a similar scale.
E.g.

归一化前，代价函数关于参数​​和​​的关系等高线图可能如下图：

而如果进行了，归一化，那么其等高线图可能就变成了下图：

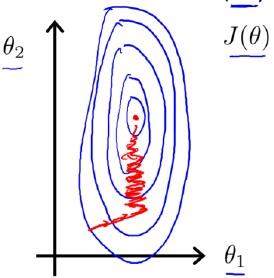
而如果进行了，归一化，那么其等高线图可能就变成了下图:

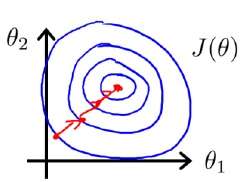
关于等高线图的变化，Andrew并没有细说原因，只是直接这么说了。一种常见的误解是：

原来和的尺度不一样，所以等高线图是狭长的，而归一化以后，大家尺度(甚至取值范围)一样了，等高线图被压扁了，所以就是一个圆形了呗。

但是问题在于，等高线图的变量(即轴)是和，而不是和！对和做的缩放，导致关于和的等高线图产生的变化根本不是直观上的那么一目了然。

本文的目标就在于把这个问题解释清楚：对和的缩放是怎么把以,为变量的等高线图变得更加圆，从而使得梯度下降效率变高的。

首先我们把问题定义一下，我们是要预测房价，目前有两个特征：
– : 面积，以平方英尺计，取值范围在0 ~ 2,000
– : 卧室数，取值范围在0 ~ 5

假设，房价是关于这两个特征的线性关系：

那么，在进行梯度下降的时候，目标最小化的代价函数(Cost Function)则为：

在缩放(scaling)前，由于的尺度比较大(0 ~ 2,000)，而的尺度小(0 ~ 5)，因此和同等大小的变化，对的影响差距巨大，即对影响要比大很多。进而，会造成对更加敏感(即的单位变化比的单位变化对的影响更大)。因此在等高线图上，在方向上更扁平，即较小的变化会造成取值的剧烈变化，而在方向上更加狭长，即较大的变化才会造成取值的较大变化。

那么缩放(scaling)以后，和的尺度是一致的，故和同等大小的变化，对的影响不再含有特征尺度上的因素，这也同样反映在上。那么在等高线图上的表现就是，在方向上等高线图会拉长，即对相较于缩放前变得"迟钝"了。

如果我们只观察和，那么二者的关系在进行特征缩放前后的图形可能如下：

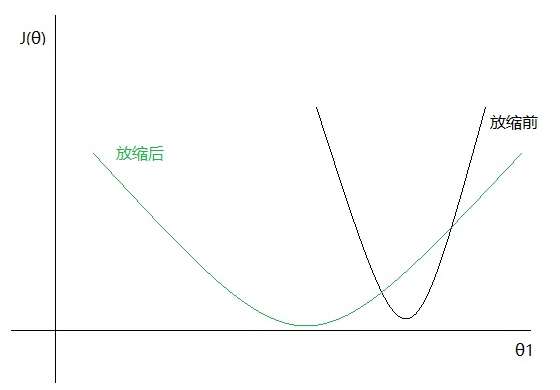
即关于更加缓和，且在上被拉长了(缩放后，参数的最优解跟缩放前几乎不会是同一个值，因此上图中的最小值点对应的值并不相同)。

因此，Andrew的缩放前后的图形，并不是在(纵轴)方向上被压扁了，而是在(横轴)方向上被拉长了！

而从梯度下降迭代上看，每次迭代使用的公式为：

注意到，每次迭代的时候，的更新幅度是和相关的，因此如果某个的尺度相较其他维度特征大很多的话，势必造成该维度对应的参数的更新非常剧烈，而其他维度特征对应的参数更新相对缓和，这样即造成迭代过程中很多轮次实际上是为了消除特征尺度上的不一致。

另一个角度，实际上就是当前的梯度方向，它和是相关的，因为对于而言，是它的参数。所以，当我们迭代更新的时候，梯度下降的方向会因特征的尺度产生剧烈变化，即在尺度大(导致梯度大)的方向上持续迭代。而这种变化显然不是迭代的目的，它仅仅是为了消除尺度差距上的悬殊。

故，因为的梯度是跟特征取值相关的，而梯度下降迭代就是不断在梯度方向上寻找最优点。所以如果特征在尺度上差距显著，那么迭代中就会有一些(甚至大量)轮次主要在抹平尺度上的差异。在理论上，如果迭代轮次足够多，仍然能够得到最优解，但在实际中往往会限定一个迭代轮次上限，可能会出现找到的解并不是最优解。

因为要抹平尺度上的差异，迭代到最优解的轮次势必增加，即表现为常说的"收敛速度慢"。

参考：http://sklearn.lzjqsdd.com/modules/preprocessing.html

https://sebastianraschka.com/Articles/2014_about_feature_scaling.html

https://scikit-learn.org/stable/modules/preprocessing.html#preprocessing-scaler