MAT1001 Midterm 错题笔记
Definition
-
\(\lim_{x\rightarrow c}f(x)\) exists means \(\lim_{x\rightarrow c^-}f(x)=\lim_{x\rightarrow c^+} f(x)\), \(f(x)\) may be or not be continuous at \(x=c\).
-
If \(f\) and \(g\) are functions defined for all real numbers, and neither \(f\) nor \(g\) is continuous at \(x = 0\), but the composite function \(f ◦ g\) can be continuous at x = 0.
Problems
\[\begin{split}
\lim_{x\rightarrow-\infty}(\sqrt{x^2+x}+2x)&=\frac{(\sqrt{x^2+x}+2x)(\sqrt{x^2+x}-2x)}{\sqrt{x^2+x}-2x}\\
&=\frac{x-15x^2}{\sqrt{x^2+x}-2x}\\
&=-\infty
\end{split}
\]
\[\lim_{x\rightarrow-\infty}x\left\lfloor\frac1x\right\rfloor=(-\infty)\times(-1)=\infty
\]
- State the Chain Rule concerning the derivative of the composite function \(f(g(x))\) at \(x = a\), then prove it precisely (by using either linearization or differentials).
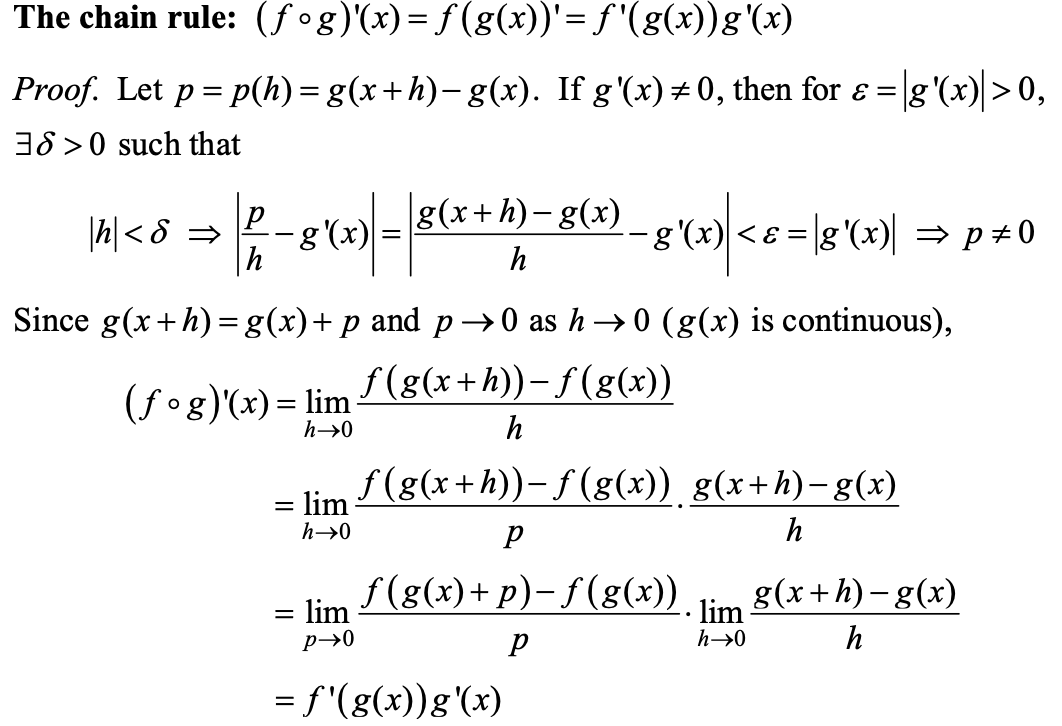
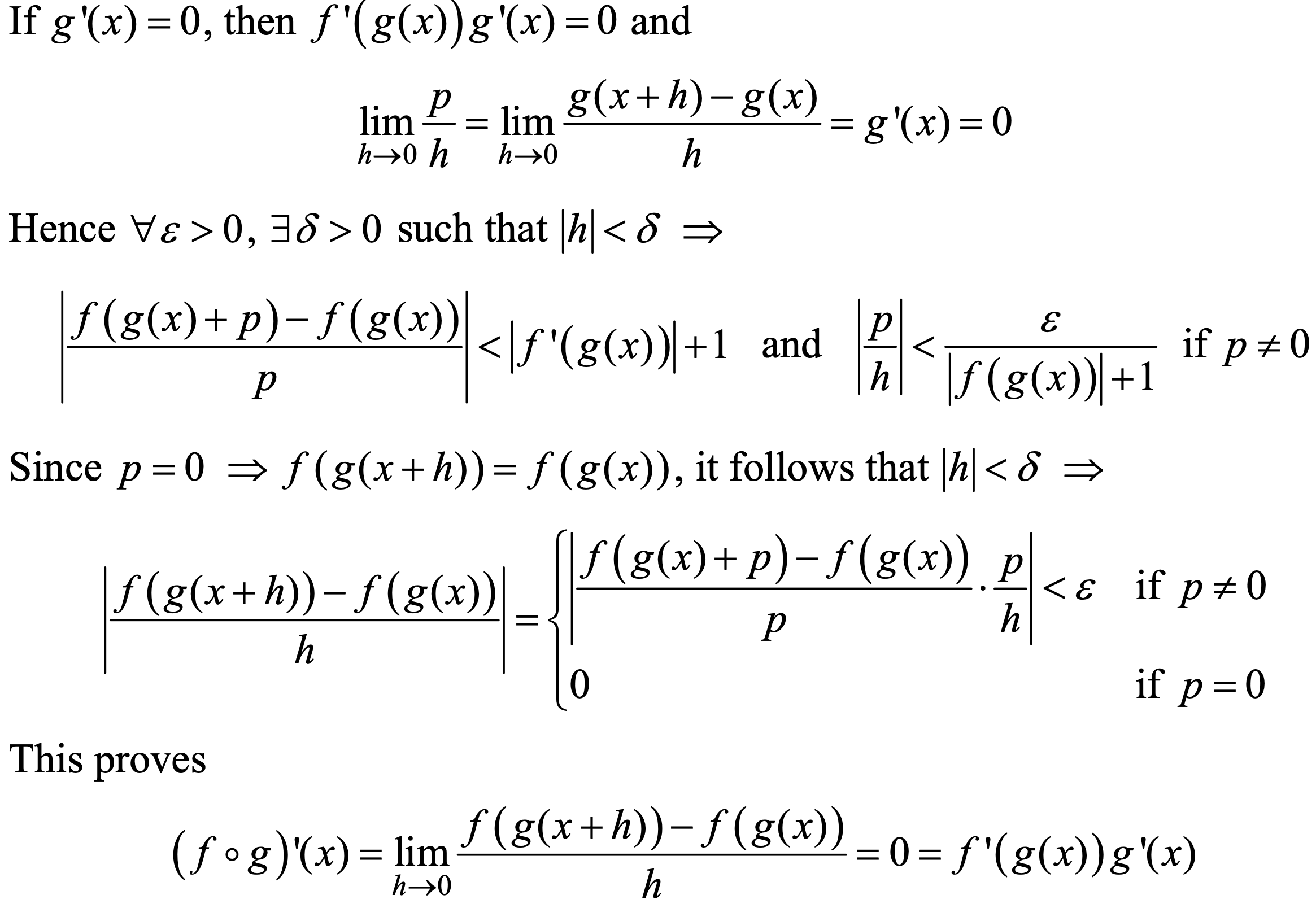


 浙公网安备 33010602011771号
浙公网安备 33010602011771号