字 符 串

Border 理论

我曾经觉得，会了 SAM 就可以解决字符串大多数问题了，但并不是。

上面那一句摘自 chenxinyang2006。

border : \(s_{[1, i]} = s_{[n - i + 1, n]}\)。

周期 ：一言以蔽之 \(s_i = s_{i + p}\)，然后 \(s[1 : n - p] = s[1 + p : n]\)。即存在一个长度为 \(n - p\) 的 border。

Lemma1：

\(s\) 的周期 \(p，q\) 若 \(p + q \leq n\)，有 \(\gcd(p, q)\) 是 \(s\) 的周期。

钦定 \(p > q\)，观察 \(p - q\) 是否是周期 \(\to\) 更损相减。

\[i > q \to s_i = s_{i - q} = s_{i - q + p} \]

\[i < p \to s_i = s_{i + p} = s_{i + p - q} \]

显然涵盖了所有情况。

Lemma2：

\(s, s'\) 分别为一个串和其的一个前缀，若 \(s, s'\) 分别有周期 \(a, b\) 且 \(b | a\) 则 \(b\) 是 \(s\) 的周期。

显然可以看出 \([1, a]\) 是由 \([1, b]\) 循环构成的，所以显然成立。

Lemma3:

\(|t| \leq \frac{|s|}{2}\) 则 \(t\) 在 \(s\) 中匹配的中匹配的起始位置构成等差数列。

小于三次无意义。

好像是可以用 \(1, 2\) 次出现位置来构造周期 \(p_{min}\) 来证明这个是等差的，很复杂。

Lemma4：

所有长度大于 \(\frac{|s|}{2}\) 的 border 构成等差数列。

\(p \leq q \leq \frac{|S|}{2}\)
这个使用 Lemma1 构造 \(\gcd(p, q)\) 这一个周期，可以得出 \(p | q\)。再利用周期来构造新的 border 证明即可。

Lemma5：

\(s\) 所有 Border 长度从大到小，可以划分为 O(logn) 段等差数列

考虑划分出 Lemma4 的内容。

然后利用 KMP 那套理论，分治子问题，大概是 \(\log_n\) 的。

Lemma6

回文串的前缀是回文串判定的充要条件是 border。

[HNOI2019]JOJO、ARC060D、ARC077D、[WC2016] 论战捆竹竿

KMP

原理：

一个串的 border 由其最大 border 本身和其 border 构成。

然后 fail -> 最长的 border.

考虑用 \(i\) 扩展 \(i + 1\) 的 border, 这个 border 是狭隘的，所以是 O(n) 的构造。

可以考虑枚举匹配到的位置 \(i\), 然后跳 border 匹配就可以试试。

P3435 [POI2006] OKR-Periods of Words

考虑求出 fail, 然后我们画个图就知道了 \(s_{1, n - fail_i} = s_{fail_i+1, n}\).

相当于扣掉一个加上去

然后我们其实可以考虑记忆化，让 \(fail_i\) 最后记忆成为 \(\min fail_j\)，也就是 \(border\) 的非零最小值就可以了

然后一直跳 border 就好了捏，拜谢 border 论！！！

失配树

无非就是 \(i \to fail_i\) 然后 \((u, v)\) 的 \(lca\) 就是最长公共 boder.

[NOI 2014] 动物园

考虑直接建出 \(i \to fail_i\) 的失配树，然后可以考虑倍增。

可以考虑直接维护小于等于一半的 fail 怎么做。

AC 自动机

貌似不太算是 border，应该算是匹配了某一前缀的该串的最长后缀，但其实是相似的，其实就是后缀。

这个有了 KMP 会很好理解。

将若干串插入 Trie 中，然后我们可以思考如何由 \(u\to v\). 来扩展 fail.

1. \(v\) 是存在的，那么 fail 无非就是 \(u\) 的 fail 再接入一个字符就可以了。

2. \(v\) 不存在，那只能接在 fail 的后面了。

我们发现 fail 后面接一个字符相当于 s 接了一个字符。那么我们想要遍历关于 \(s\) 的字串，那么找出来 fail 就是必要的。因为 \(i\) 这个位置连接的 fail 才可以产生贡献，所以说匹配的时候要一直跳 fail, 相当于一个终止节点.

然后 fail 树的子树内点的个数就是出现次数.jpg，这个其实很 SAM。

多串匹配 ：

我们考虑一直跳 fail 然后发现有个地方有串串就直接加上就行了。

扩展 KMP :

不会 Z 函数，但是感觉还是 SAM 比较 good，可以先 skip。

Manacher：

考虑添加了若干 \(#\) 来把所有字符串变为奇回文串，放在自互传中间。

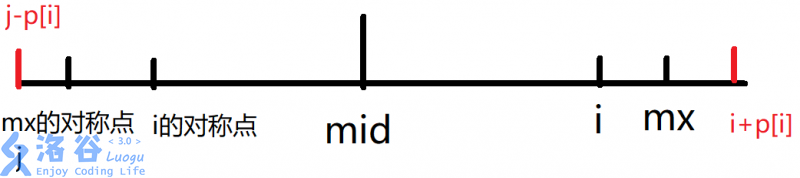
有图的主播，牛逼！！

考虑求出一组 \(mx' \to mx\) 的回文串，然后最好是最近的可覆盖的。

那么 \(p_{i'}\) 和 \(p_i\) 表示扩展出来的回文串，可以直接暴力求，亏贼！

注意到 \(p_i'\) 和 \(p_i\) 求得时候有一个 \(i\to mx\) 的限制，这个地方取 min, 剩下的可以直接暴力求来拓展。

然后求答案是注意一些 \(\text {corner case}\)

int init () {
	cin >> str;
	int len = strlen(str), p = 2;
	s[0] = '~', s[1] = '#';
	rep(i, 0, len - 1) s[p ++] = str[i], s[p ++] = '#';
	s[p] = '%'; return p;
}
int manacher () {
	int len = init(), mid = 1, mx = 1, ans = -1;
	rep(i, 1, len - 1) {
		if (i < mx) p[i] = min(mx - i, p[2 * mid - i]);
		else p[i] = 1;
		while(s[i - p[i]] == s[i + p[i]]) p[i] ++;
		if (mx < i + p[i]) mx = i + p[i], mid = i;
		ans = max(ans, p[i] - 1);
	}
	return ans;
}

写 hash 没有 define int long long 的人生是失败的。

PAM

学过的这么多 AM 有没有思考过这些为啥都是用后缀，因为后缀牵扯到的都是与连续子串相关的问题，对目前是有用的，可以直接增量构造法！

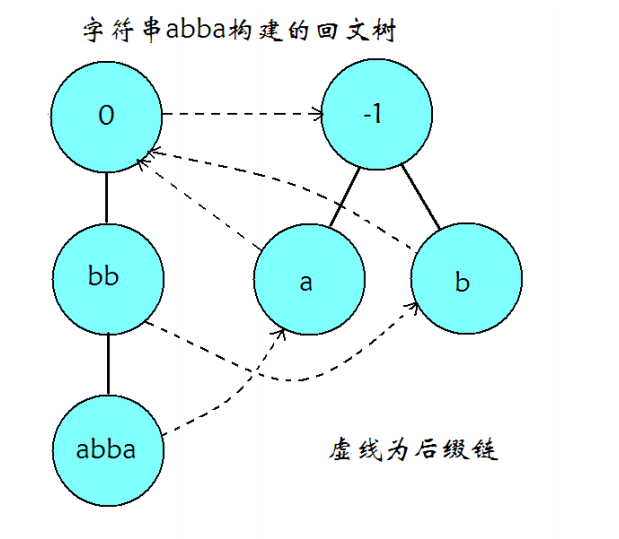
一个节点的 fail 指针指向的是这个节点所代表的回文串的最长回文后缀。

这个是自动机经典操作，其实感觉真的很像 SAM + ACAM。

考虑先从 last 开始跳 fail，找的一个合法的地方，然后再看是奇回文和偶回文。偶回文的 fail 都指向奇回文，这样奇回文中间就可以扩展了。

如果指向一个奇根那就说明没有匹配，你太捞了

• 线性状态数证明

即是证明本质不同回文串个数是 \(|S|\)。

考虑 PAM 的形状，你每次只新建一个节点不是咩，这不是 \(O(1)\) 是啥，是呱！

那时间复杂度怎么证明？

考虑增量构造方法，每次跳 fail 后对应节点在 fail 树的深度 -1，而连接 fail 后，仅为深度 + 1。

然后只会加 \(n\) 次深度，然后我们如果跳了一个节点就走不回去了，所以是 \(O(n)\) 的，呱呱呱！！！

struct PAM {
	int tot;
	int ch[N][C], fail[N], len[N], cnt[N], lst;
	PAM () {
		tot = 1, fail[0] = 1, fail[1] = 1, len[1] = -1;
	}
	int getfail (int x, int i) {
		while(i - len[x] - 1 < 0 || s[i - len[x] - 1] != s[i]) x = fail[x]; 		
		return x;
	}
	void insert (char c, int i) {
		int x = getfail(lst, i), p = c - 'a', np;
		if (! ch[x][p]) {
			np = ++ tot, len[np] = len[x] + 2;
			int y = getfail(fail[x], i);
			fail[np] = ch[y][p], cnt[np] = cnt[fail[np]] + 1, ch[x][p] = np; //这里 np 好像要放在最后，不然 fail 会设置错误。
		} lst = ch[x][p];
	}
} pam;

后缀排序。

其中 \(SA_i\) 代表的是排名为 \(i\) 的后缀的起点, \(rk_i\) 表示 \(i\) 在所有后缀中的排名。

LSD基数排序: 考虑将最后一位分类塞进桶里，在按此一次取出，然后再按倒数第二位分类，循环下去即可。

如何构造？考虑利用排序好的较短后缀来排序长后缀。

考虑由 \(len \to 2 * len\)。分为前后两个部分来比较排序。我们可以考虑每次对前半部分进行排序，然后利用后半部分再比较即可。每次先计算出前半部分的排名，然后我们依次可以推出后面一部分的排名。然后将其变为二元关系。然后用前缀部分作为第一关键字，后半部分作为第二关键字，做基数排序即可。但是这个是基数排序，所以要先按 \(2\) 来，老铁懂吗？

大概是 \(s[i, i + len - 1], s[i + len, i + len * 2 - 1]\) 这一些都在表内，所以可以计算，有一些要注意补 0。

inline void basic_sort () {
	for (int i = 1; i <= m; i ++) buc[i] = 0;
	for (int i = 1; i <= n; i ++) ++ buc[rk[i]];
	for (int i = 1; i <= m; i ++) buc[i] += buc[i - 1];
	for (int i = n; i >= 1; i --) sa[buc[rk[tmp[i]]] --] = tmp[i];
}
inline void suffix_sort () {
	for (int i = 1; i <= n; i ++) rk[i] = s[i], tmp[i] = i;
	basic_sort();
	for (int l = 1, p = 0; l <= n && p < n; m = p, l <<= 1) {
		p = 0; d (int i = n - l + 1; i <= n; i ++) tmp[++ p] = i;
		for (int i = 1; i <= n; i ++) if (sa[i] > l) tmp[++ p] = sa[i] - l;
		basic_sort(), swap(rk, tmp), rk[sa[1]] = p = 1;
        for (int i = 2; i <= n; i ++)
            rk[sa[i]] = (tmp[sa[i]] == tmp[sa[i - 1]] && tmp[sa[i] + l] == tmp[sa[i - 1] + l]) ? p : ++ p;
	}
}

height数组

定义：\(\text{height_i = lcp(i, i - 1)}\)，规定 \(i\) 和 \(i - 1\) 都是指的后缀。

那么 \(\text{lcp(i, j)}\) 即为 \(\text{height}\) 的区间最小值。

考虑如下性质：令 \(h_i= height_{rk_i}\)，那么满足 \(h_i \geq h_{i - 1} - 1\) 这些是考虑到退位的一些性质，于是就可以 \(O(n)\) 建了。

void getH () {
	int pos, len = 0;
	for (int i = 1; i <= n; i ++) {
		if (len) len --;
		pos = sa[rk[i] - 1];
		while (a[i + len] == a[pos + len]) ++ len;
		h[rk[i]] = len;
	}
	return ;
}

后缀自动机。

endpos : 一些字符串的终止位置。

link ：不在同一 endpos 的最长后缀，注意最长后缀是可以作为子串出现，并不是该串的严格后缀。

构建，考虑维护上一个状态的 \(last\), 然后我们新建一个节点 \(cur\)。

int insert (int p, int c) {
	if (ch[p][c] && len[ch[p][c]] == len[p] + 1) return ch[p][c];
	int cur = ++ cnt, flag = ch[p][c]; len[cur] = len[p] + 1; // newnode
	while (! ch[p][c]) ch[p][c] = cur, p = fa[p];
	if (! p) return fa[cur] = 1, cur; // case 1, nothing
	int q = ch[p][c];
	if (len[p] + 1 == len[q]) return fa[cur] = q, cur; // case2 : 相当于仅仅是产生了新的一条出边，endpos 是相似的。
	int cl = ++ cnt; cpy(ch[cl], ch[q], S);
	len[cl] = len[p] + 1, fa[cl] = fa[q], fa[q] = fa[cur] = cl; // 此时属于了不同的 endpos 即是不符合 case2，所以要分裂。
	while (ch[p][c] == q) ch[p][c] = cl, p = fa[p];
	return flag ? cl : cur;
}

分三类，第一种是没有，说明这个是孤儿，直接指向就好了。第二种是 \(len_p = len_x + 1\)，此时 p 是我们 \(\text parent\) 树上的祖先，那我们找不到啥，这个 \(x\) 就是最优，直接将 \(x\) 设为后缀链接即可。这两种大概是先前的。

第二类的证明，首先祖先都是自己的字串，考虑到要保证 \(endpos_u \in endpos_{suf}\)，如果是一个祖先上横叉走出去的不同 \(c\) 的边我们是这个是错误的，那我们找到的第一个 \(x\) 那显然可以保证。

不然就说明，\(x\) 有不同长度的字串来表示，那我们只想要的是第二种，那我们直接弄出来第二种 \(len_{clone} = len_p + 1\) 表示找到符合 2 的 task，的即可，但是注意到，我们这个 \(x\) 还要拆出来，然后将 \(clone\) 设到 suffix links 上，本质上只是对于第二种情况的拙劣模仿。

事实上，SAM 暴力跳 parent 是有一个自然根号的。

\[\sum |szcol_x| = len\sqrt{len} \]

用这个可以解决 CF204E，每次暴力修改没被修改过的 ancestor，然后累加返祖链的累加值即可。

杂题总结

• CF808G Anthem of Berland

考虑到匹配的形式，一种是字符串没有重叠，那就硬匹配。

那么另一种就考虑在匹配完后怎么移位，那就是明显的 border。

• P5840 [COCI2015]Divljak

• CF710F String Set Queries

• P4762 [CERC2014]Virus synthesis

• P4287 [SHOI2011]双倍回文

• P3649 [APIO2014] 回文串

• P5446 [THUPC2018]绿绿和串串

还有但是先放放。

alex-wei

做题参考