二叉堆、BST 与平衡树

二叉堆

一种父节点与子节点间存在特殊关系（一般为单调性）的完全二叉树，分为两种：大根堆和小根堆。前者的性质为父节点大于子节点，后者反之。

例题：

P3378【模板】堆

P1090 合并果子 Normal

P6033 合并果子 Hard

P1628 合并序列

P2278 [HNOI2003] 操作系统

二叉堆主要支持以下操作：push，pop，top 和 size。

---

1. top

不多说，返回堆顶元素即可。

int top() {
  return basic[1];
}

2. size

在 push 与 pop 操作时，使用一个变量 tot 记录当前节点数量，询问时输出 tot 即可。

int size() {
  return tot;
}

3. push

往二叉堆中加入一个数时，首先加入树的数组末端，然后按照堆的性质自下而上修复二叉树，使其满足性质。

代码如下：

void push(int x) {
	basic[++tot] = x;
	modify(tot);
}
void modify(int x) {
	if (x == 1 || basic[x] > basic[x >> 1]) {
		return;
	}
	swap(basic[x], basic[x >> 1]);
	modify(x >> 1);
}

4. pop

将元素弹出二叉堆时，如果直接删除堆顶元素，会造成二叉树的分裂，产生大麻烦。所以，考虑将堆顶元素与堆底元素互换，再自上而下修复二叉树。

void pop() {
	swap(basic[1], basic[tot--]);
	repair(1);
}

void repair(int x) {
	if ((x << 1) > tot) return;
	int tar = x << 1;
	if ((x << 1) + 1 <= tot) {
		tar = (basic[x << 1] < basic[(x << 1) + 1] ? x << 1 : ((x << 1) + 1));
	}
	if (basic[x] > basic[tar]) {
		swap(basic[x], basic[tar]);
		repair(tar);
	}
}

与自下而上修复不同，在交换父节点与子节点的值时，策略为交换子节点中较大的一个值。

注意在 repair 时要考虑数组是否越界。

tip : 堆也可作为一种排序方式。理解了上述代码后可尝试自己写下这题。

接下来看看 STL 中的二叉堆—— priority_queue。

操作与平常的 STL 没什么区别，注意默认大根堆，建小根堆应这样写： priority_queue<typename, vector<typename>, greater<typename> >。

时间复杂度：push 与 pop $ O(\log{n})$ ， top 与 size $ O (1)$ 。

对顶堆

本质上是大根堆与小根堆的结合，用于动态维护数列中第 $ k $ 大 / 小的数。

例题：

P1168 中位数

P1801 黑匣子

以 P1168 为例：

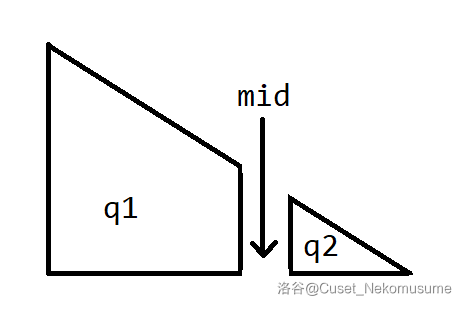
维护一个大根堆 $ q1 $ 与一个小根堆 $ q2 $ 和中位数 $ mid $ ，保持 $ q1 $ 与 $ q2 $ 的元素数量相等，维护过程中不断交换 q1.top 、q2.top 与 mid ，数列元素数量为奇数时输出 mid 即可。

二叉搜索树，\(\textbf{BST}\)

BST 的特征：

1. 每个节点有唯一键值。
2. BST 上以任意节点为根的子树都是 BST。
3. BST 中任意节点的键值都比它左子树所有节点的键值大，比它右子树所有节点的键值小。即若用中序遍历整棵 BST 将得到的是一个有序序列。

若用给定的序列按照特征 (3) 建树，将得到的是一棵唯一的 BST。

二叉树的不平衡率 \(\alpha\)

含义为其左子树或右子树的占比，取值范围为 \([0.5,1]\)。\(\alpha\) 越大，代表该二叉树越不平衡。

树堆，\(\textbf{Treap}\)

核心思想：用优先级（大小根堆）的思想来维护二叉树的平衡性。

根据这个思想，我们可以得到：若每个节点的键值、优先级均已确定，那么建出的二叉树的形态是唯一的。

这种把树和堆思想结合在一起的便叫「树堆」，\(\text{Treap}\)。

有旋 \(\text{Treap}\)

有旋 \(\text{Treap}\) 插入节点的过程分两步：

1. 先将新节点的键值插入一个空的叶子节点。
2. 为该叶子节点分配一个随机的优先度，然后按