P10648 题解

题目传送门 P10648 Island Alliances

感谢机房大佬 @Jeslan 的指教。

首先读题，发现题中说“一但同意了联盟，则两个岛屿所在联盟立即并成一个联盟”，那么首先想到的做法就是并查集，那么，这题合并联盟的部分就做完了。这么简单?(bushi)

接下来就是这题的难点：如何维护每个联盟不能结成联盟的岛屿？在上面的并查集中，我们每次合并都会选定一个点为该并查集的代表，那么，可以想到，在合并联盟时把所有非代表结点所不能结盟的岛屿都移至代表上，这样在合并时就只需考虑两个待合并联盟的代表了，下面来举个栗子：

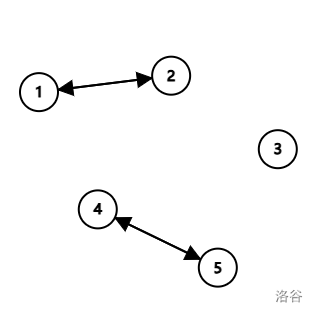
上图中，双向边所连接着的是敌对的岛屿。若此时把岛屿 $2$ 与岛屿 $3$ 合并，就可以将 $1$ 与 $2$ 所连接的边转移到 $3$ 上（合并时 $3$ 作为代表），并删除 $1$ 与 $2$ 所连接的边，如下图：

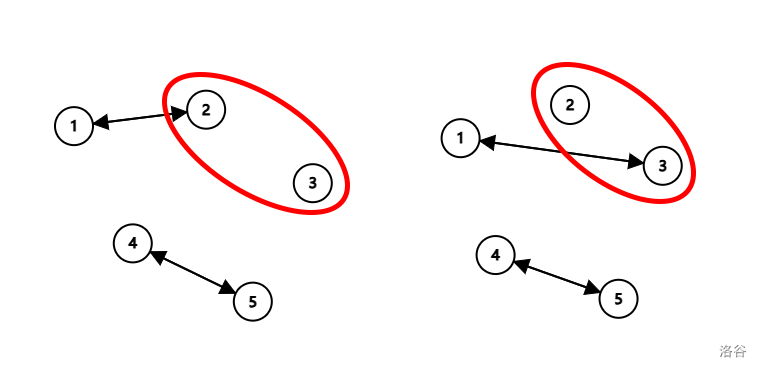
若此时再将 $2,3$ 与 $5$ 合并，选定 $5$ 为代表，同理，如下图：

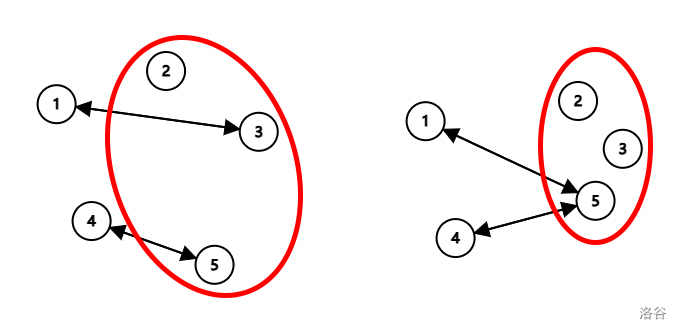
此时若将 $1$ 和 $2,3,5$ 合并，只需查找 $2,3,5$ 的代表 $5$，发现 $1$ 和 $5$ 为敌对岛屿，合并失败。

算法的思想就到这了，下面来说说实现。

本题的核心就在于转移敌对边，普通 vector 或链式前向星存图无法做到高效地转移边，那么就考虑使用 set 保存边，合并时使用启发式合并。

奉上代码一份：

#include <bits/stdc++.h>
#include <bits/extc++.h>
using namespace std;
using namespace __gnu_pbds;
 
typedef long long ll;
typedef long double ld;
typedef unsigned long long ull;
typedef pair<int, int> pii;
 
const int MAXN = 1e5 + 5;
int fa[MAXN];
 
int getfa(int x) {
    if (fa[x] == x) return x;
    return fa[x] = getfa(fa[x]);
}
 
void merge(int x, int y) {
    fa[getfa(x)] = getfa(y);
}
 
//以上两个并查集核心函数
 
set<int> s[MAXN];//set 保存每个岛屿/联盟所敌对的岛屿/联盟
 
int n, m, q;
 
int main() {
    cin >> n >> m >> q;
    for (int i = 0; i <= n; i++) {
        fa[i] = i;
    }//初始化并查集
    for (int i = 1; i <= m; i++) {
        int u, v;
        cin >> u >> v;
        s[u].insert(v);
        s[v].insert(u);//互相敌对
    }
    for (int i = 1; i <= q; i++) {
        int u, v;
        cin >> u >> v;
        int fau = getfa(u);
        int fav = getfa(v);
        if (s[fau].size() > s[fav].size()) swap(fau, fav);//启发式合并，小的合并入大的
        if (s[fau].find(fav) == s[fau].end()) {//如果找不到 father of u，即 u 与 v 不敌对，此时可合并
            printf("APPROVE\n");
            for (auto x : s[fau]) {//将小集合所有敌对边转移到代表上
                s[fav].insert(x);
                s[x].erase(fau);//删除原有边
                s[x].insert(fav);
            }
            merge(fau, fav);//并查集合并
        } else {
            printf("REFUSE\n");
        }
    }
    return 0;
}