Fall with Tree(hdu7046)

Fall with Trees

https://acm.hdu.edu.cn/showproblem.php?pid=7046

题意：

​ Fall想画一棵完美的二叉树。

​ 我们首先规定树中具有相同深度的所有节点在平面上也具有相同的y坐标。将具有相同深度的节点定义为相同级别的节点，则完美二叉树具有四个属性。

​ -这是一个完整的二叉树。

​ -每个相邻标高上两个节点的y坐标之间的差值为常数。

​ -同一级别上两个相邻节点的x坐标之间的差是恒定的。

​ -每个节点的x坐标是其子节点的x坐标的平均值。

​ Fall已经绘制了这个二叉树的根节点及其左右子节点。现在Fall打算画出总共k层，然后把二叉树砍掉，然后粘贴到墙上，所以他想知道这个完美二叉树所有节点的凸包面积是多少。

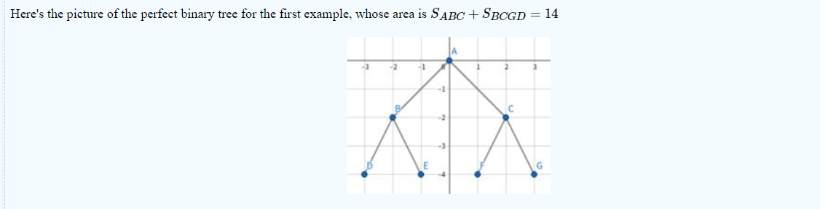
思路：暴力求解，找到公式

代码：

#include <bits/stdc++.h>
using namespace std;
#define int long long 
#define mod 998244353
double qpow(double x, int y)//快速幂 
{
    double ans = 1;
    while (y){
        if (y & 1) ans = ans * x;
        x = x * x;
        y >>= 1;
    }
    return ans;
}
signed main(){
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int t;
    cin>>t;
    while(t--){
        int rx,ry,x1,y1,x2,y2;
        int n;
        cin>>n;
        cin>>rx>>ry>>x1>>y1>>x2>>y2;
        double h=abs(ry-y1);//算出高 
        double k=2*abs(rx-x1);//算出第二层的宽度
		//第n层宽度为k*(2-2^(2-n)); 
		//公比为1/2； 
		//第二层的宽度到n层宽度和为2k*(n-1)-k(1-(1/2)^(n-1))/0.5;
		//第三层的宽度到n-1层宽度和为2k*(n-3)-k*0.5(1-(1/2)^(n-3))/0.5;
        double sum=0;
        if(n>2){
            double k1=2*k*(n-1)-k*(1-qpow(0.5,n-1))/0.5;
			double k2=2*k*(n-3)-k*0.5*(1-qpow(0.5,n-3))/0.5;
			double res=(k1+k2);
            sum=(h*k)*0.5+res*h*0.5;
        }
        else sum=(h*k)*0.5;
        printf("%.3f\n",sum);
    } 
    return 0;
}