luogu P9552 浣熊的小溪 题解

原题链接

比赛时有事，晚进早退，就打卡了一下 T1，估计起码有橙（怎么可能是红）。。。

这是一篇有详细过程的成长类题解。

题意（还原向）

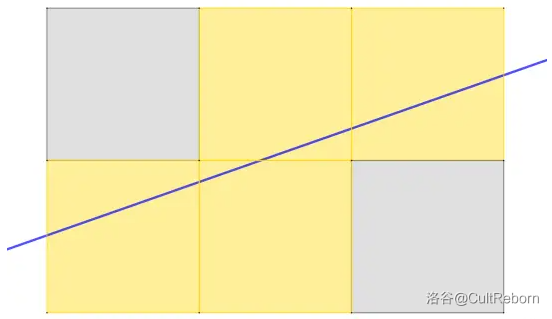
设 \(f(n,m)\) 表示一条直线最多能穿过 \(n\times m\) 的网格图的格子数。

1. 给定 \(n,m\)，求 \(f(n,m)\)；
2. 给定 \(n,m,Q\)，找到 \(n'\ge n,m'\ge m\)，满足 \(f(n',m')\ge Q\)，且 \(n'\times m'\) 尽可能小。求 \(n'm'-nm\) 的最小值对 \(998244353\) 取模的结果。数据保证 \(f(n,m)<Q\)。

题目说得很清楚。

思路（逐步向）

问题一：

对于问题一，我们可以先寻找规律，通过在草稿纸上我们画图得到这样的结果：

m\n	1	2	3	4	5	6
1	1	2	3	4	5	6
2	2	3	4	5	6	7
3	3	4	5	6	7	8
4	4	5	6	7	8	9
5	5	6	7	8	9	10
6	6	7	8	9	10	11

猜测 \(f(n,m)=n+m-1\)。

证明：

考虑数学归纳法：

1. \(m=1\) 时，直线只能穿过一行或一列的格子，总数为 \(n+m-1\)，\(n=1\) 同理。
2. 假设：对于任意的 \(n×m\) 的网格图，一条直线最多能穿过 \(n+m-1\) 个格子。试证明对于 \((n+1)\times m\) 和 \(n\times(m+1)\) 的网格图也成立。
3. 对于 \((n+1)\times m\) 的网格图，假设直线从左上角顶点到右下角顶点，穿过了 \(n\times m\) 的网格图的 \(n+m-1\) 个格子，然后再穿过额外的一行格子，总数为 \(n+m-1+1\)。
4. 又因为 \(n\) 和 \(m\) 互换后不影响最后的答案，所以 \(n×(m+1)\) 的网格图同理。
5. 综上所述，可以证明一条直线最多能穿过 \(n×m\) 的网格图的格子数是 \(n+m-1\)。

命题得证。

于是问题一优雅地解决了。

问题二：

至于问题二，需要我们使用一些数学知识。

1. 令 \(n>m\)，结果不变；
2. 此时易知 \(Q\geq n\geq m\)；
3. 由问题一的结论我们知道 \(Q=f(n',m')=n'\times m'-1\)；
4. 要求 \(n'm'-nm\) 的最小值，又由于 \(n\) 和 \(m\) 为定值，所以只要求 \(n'\times m'\) 的最小值；
5. 根据均值不等式，当 \(n'=m'\) 时，\(n'\times m'\) 最大；当 \(n'\) 和 \(m'\) 之间相差越大时，\(n'\times m'\) 最小。
6. 由于我们已经规定 \(Q\geq n\geq m\) 了，让 \(n'\) 和 \(m'\) 之间相差最大的做法，就是让 \(m'=m\) 不变，增加 \(n'\) 的值；
7. 又 \(Q=n'\times m'-1\)，所以 \(n'=Q+1-m'\)，\(m'=m\)。最终的答案即为 \((Q-m'+1)\times m-n\times m\)。
8. 注意取模。

推理结束，接下来是代码时间……

代码（丑陋向）

30pts Code：

(点击上方超链接可查看评测记录)

事实证明第二问的代码没有那么好写，下面是一篇不良代码，我们看一下哪里出了问题。

1    else {
2	  cin >> Q;
3	  n %= mo; m %= mo; Q %= mo; 
4	  if(n < m) swap(n,m);	  
5	  n2 = (Q - m + 1) % mo;
6	  cout << (n2 * m - n * m) % mo << "\n";
7	}

1. 第三行和第四行的顺序颠倒了——我们不能先取余再交换，因为取余后会改变大小关系。
2. 因为取余后会改变大小关系，所以第五行和第六行会出现负数，这是不允许的，所以需要在括号内加上模数，来规避错误的负数。
3. 另外，第六行的括号内需要减去一个二次的多项式 \(n\times m\)，必须要加上 \(998244353\times998244353\) 才能合法计算，于是我们不得不使用乘法分配律，把答案 \((Q-m'+1)\times m-n\times m\) 换成 \([(Q-m'+1)-n]\times m\) ，这样只用在括号内加一次模数就好了。

AC Code:

(点击上方超链接可查看评测记录)

#include<bits/stdc++.h>
using namespace std;
const int mo = 998244353;
long long T,n,m,op,Q,n2,m2;
int main(){
  cin >> T; 
  while(T--){
  	cin >> op >> n >> m;
  	if(op == 1)
  	  cout << (n + m - 1) << "\n";
	else {
	  cin >> Q; Q %= mo;
	  if(n < m) swap(n,m);	  
	  n %= mo;  m %= mo;
	  n2 = (Q - m + 1 + mo) % mo; 
	  cout << ((n2 - n + mo) * m % mo) % mo << "\n";
	}
  }
  return 0;
}

创建博客：[2023.08.17 16:25]

完成题解：[2023.08.17 18:58]

上传题解：[2023.08.17 19:28]

修改题解：[2023.08.17 23:00]

简化题解：[2023.08.18 18:55]