强连通分量 （Kosaraju）

问题描述

求一个有向图中的强连通分量的个数。

---

解题思路：

明确一下强连通的定义：

• 存在 $i$ 和 $j$ 两点，使得 $i$ 和 $j$ 互相可抵达。

根据强连通的定义，我们可以得出，若对存在强连通的图进行置换（将所有有向边反转），那么强连通任然是强连通的。
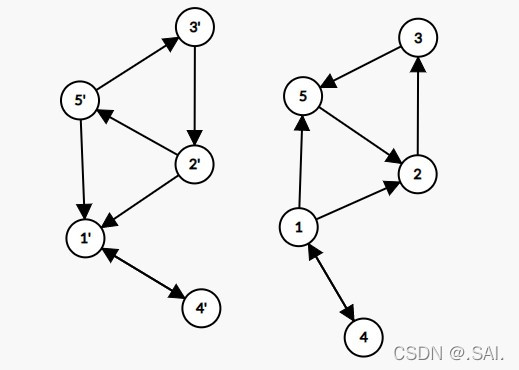
这里我们先给出一张存在两个强连通的图以及它的置换图。

接下来是算法的步骤：

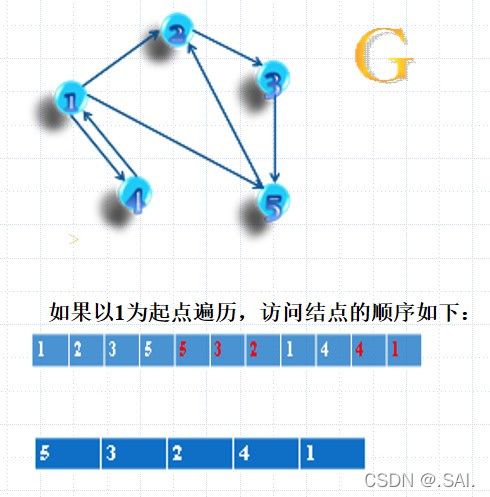
1. 先任意找到一个点对原图进行 $dfs$ 遍历一遍，然后将每个节点出栈的顺序记录。这一步骤保证了接下来算法求出的强连通分量是按照拓扑排序给出的。

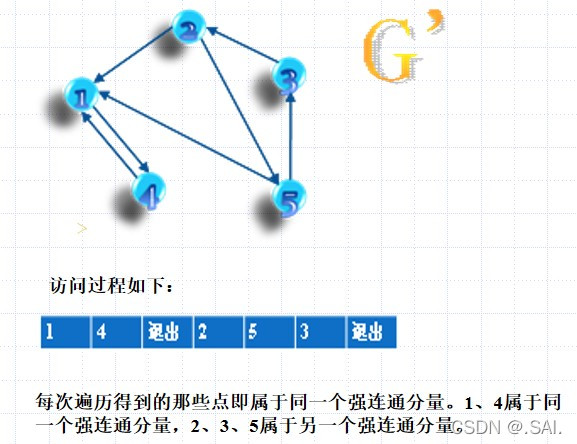
2. 按照第一步对 $dfs$ 的出栈记录倒序取出记录的点，将这些取出的点作为起点对置换图进行 $dfs$ 遍历，每一次遍历求出的点就是同一个连通分量的（因为在置换图中 $i$ 和 $j$ 若非强连通是无法从 $i$ 到 $j$ 的）。

---

CODE:

#include <iostream>
#include <vector>
#include <deque>
#include <cstring>
using namespace std;
int n,m,t,ans;
vector<int> g[100010],g2[100010];
deque<int> q;  //用双端队列存储出栈顺序，避免倒序的麻烦
bool vis[100010]={false};
void dfs1(int s)
{
	vis[s]=true;
	for(int i=0;i<g[s].size();i++)
	  {
	  	if(!vis[g[s][i]])
	  	  dfs1(g[s][i]);
	  }
	q.push_front(s);
	return ;
}
void dfs2(int s)
{
	vis[s]=true;
	for(int i=0;i<g2[s].size();i++)
	  {
	  	if(!vis[g2[s][i]])
	  	  dfs2(g2[s][i]);
	  }
	return ;
}
int main()
{
	cin>>n>>m;
	int a,b;
	for(int i=1;i<=m;i++)
	  {
	  	cin>>a>>b; 
	  	g[a].push_back(b);
	  	g2[b].push_back(a);  //建置换图
	  }
	for(int i=1;i<=n;i++)
	  {
	  	if(!vis[i])
	  	  dfs1(i);
	  }
	memset(vis,false,sizeof(vis));
	while(!q.empty())
	  {
	  	if(!vis[q.front()])
	  	  dfs2(q.front()),ans++;
		q.pop_front();
	  }
	cout<<ans;
	return 0;
}