noip 计划
错题本
记得清空临时数组之类的东西!以及一些需要重复使用的数据结构,特别是 堆和栈,树状数组等。
改代码的时候 or 给数组里加东西的时候,考虑是否会对程序其他环节造成影响。
大样例全过会暴0。
检查每个数组有没有开小,看看程序会不会访问到超过数据范围的地方。
两个不同的错误拼在一起居然让我过了样例,警钟敲烂
一定要注意算法常数的影响!!!
线段树,分块——可通过小区间的答案合并,得到大区间的答案。
原来是有个数组忘记放结构体里了,导致另一个数组排序后顺序变了而这一个没变
大 int 相乘,前面一定要加 1ll*
支持负下标的数组 cnt:
int _cnt[600010];
int *cnt=_cnt+300000;
dp 考虑省略无效转移,无效状态,优化状态 P5017
考虑是否具有单调性
计数题注意:是否覆盖所有可能情况,是否算重,如何去重
浮点数大小判断的eps不要设得太小,大概 1e-8~1e-10即可。
写代码前一定要思路清晰,否则容易犯一些逻辑上的zz错误,还能过样例。
有向图找环是在栈中的点,而不是访问过的点。
在想清楚前或长久挣扎前,不要轻易舍弃一个想法or做法。 世末歌者
容斥转换条件。
写代码切忌心急!!!!随意!!!
函数 or 循环 retun,continue,break 前一定要检查是否有一些必做操作没做完然后才能退出!!!
思考无用状态的存在,变量的初值,是否会对程序造成影响,是则要避免。
注意每个变量的值域,以及真正有意义的值域,需要把无意义的情况排除干净。
R13 C. 数据结构
long long 一定要开够!!!特别是一些不起眼的临时变量,还有结构体里的属性!!!实在不行就 define int long long 吧!
代码一定要静态查错 一次,避免出现 v 写成了 u 之类的错误。
无向图基环树找环,一定要一找到就退出遍历,否则环会被访问两次!
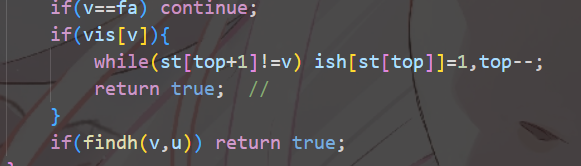
取模的时候,累加器一定不能写 +=!
对图上信息进行差分约束要注意,差分约束建出来的图,与原图不是一张图!P5590
先对整个问题分讨清楚了,再进行细节部分的思考。 AT_arc203_c [ARC203C] Destruction of Walls *2
分讨一定不能少T667229 R15 - 我想不出有趣的题目名称了所以这题就叫排列
我的代码没用到这个性质,不代表 不具有这个性质不会对我的代码产生影响 T667229 R15 - 我想不出有趣的题目名称了所以这题就叫排列
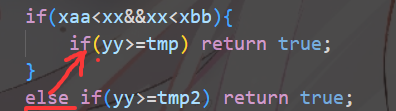
第一个 if 的大括号一定要加上,否则后面的 else 就对上里面的 if 了。
考虑 corner case 是否会对 dp 的转移产生影响。P13391 [GCJ 2010 #1A] Make it Smooth
今天比赛犯了很多错误,包括:T669096 R16 - B「绀碧绝音」 代码循环中 b 打成了 n;T669097 R16 - C「记忆的回响」 代码中正负号打反,少写了判断条件。
感觉这都是代码“惯性”导致的,感觉写代码写上头了就会不清醒,会有一个惯性,凭着很浅的理解直接写出来。这样子就很容易犯错误,如果不想静态查错的话,就要保证写代码的时候头脑一直在线,一直关注着当前写的这行代码,对不对,有什么道理,会不会少了什么之类的;(这样应该能减少犯错概率吧,速度也不会慢)
检查数组是否开够。
思考的时候,一定要记得原题目是什么,不要漏条件想歪了。
dev-C++ 会默认 inline 的返回值为 int,因此形如 inline find(int x){} 这样定义的函数在本地会通过编译,但交上去会 CE!!!一定要小心!为了避免奇怪的原因导致最终 CE,要加上编译命令 -Wall。
线段树分治,一定要在一访问节点的时候就马上下放信息(记得叶子节点也要下放,否则可能会有一些该更新的位置没更新到,区间在线段树上的体现相当精密),在每次 return 前都要撤回。
写代码的时候一定要注意 coner case!
写 dp 的时候注意循环顺序,转移顺序对对答案是否有影响。
全概率公式 :
\(P(A_i)\) 就是概率 dp 的初始状态,\(P(B)\) 就是概率 dp 的后继状态,\(P(B|A_i)\) 就是从当前状态转移到后继状态的概率。
思考问题不能想当然,T685045 10.26 T2 - マシュマリー,要考虑操作是否还具有 任意度,看看是否还需要分讨 or 贪心。
CSP-S2025 T2 检查数组是否开够,不仅要回归题目对照数量级,还要考虑自身代码需要用到多少(在本题中,我多用了 \(k\) 个虚点,因此数组大小应开到 \(n+k\),不要因为 \(k\) 很小就给忽略掉了)(双向边链式前向星要开两倍之类的)。*2 判负环的时候也要考虑引入的虚点,超级原点的影响。
卡常很重要,因为常数丢分很崩溃。但是快读别写错了,判断正负号的时候一定要判一下是不是 - 号,否则会把空格也弄进去了。
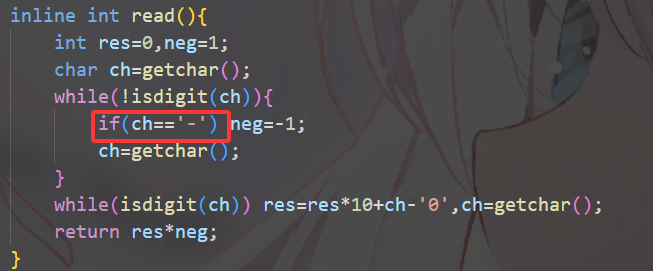
(这个快读,太神秘了,不加这个判断本地 ac 交上去 wa,小心!!!!)
写贪心前一定要证明 or 简单地 hack 一下。

注意这种小循环当中,循环变量的意义到底是什么,调用的时候要不要对其映射(k 还是 id[k] ),注意这种小细节。

不 define int long long 是好习惯,但是这种非常犄角旮旯的临时变量,如果值会爆 int 一定要注意!大样例挂了,可以先 define int long long 看一下是不是 ll 没开够,节省找错误的时间。
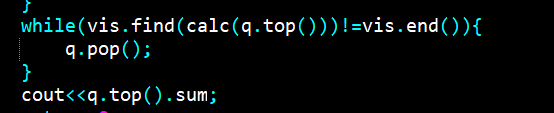
对堆进行懒删除的时候,一定要把下放操作和访问 top 的操作严格绑定!每次访问都要下放别忘了。

千万别将 1e12 这种浮点数直接写进整数运算,无论加没加 1ll 都会丢失精度!要这么写:
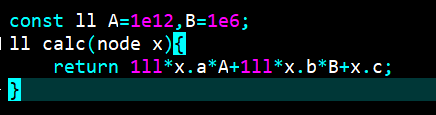
map 和 set 等判断相等的机制是利用 <,当 a<b,b<a 同时成立时判 a=b。 因此对于结构体类型的 set 和 map 使用起来一定要注意,因为重载后的 < 号可不一定是你所希望的相等条件!

函数内的局部变量,也一定要赋初值!
记录
进行大整数之间的乘除 or 累加运算时,时刻注意是否爆 long long
将元素排好序后,注意此时访问对应下标的元素并非原始编号下的元素!!如需访问,需记录原始编号,并对原始序列做一个拷贝一遍利用原始编号访问。
DP 考虑尝试刷表法:\(f_{i,j}\) 不好确定从哪个 \(i-1\) 转移,那就用 \(f_{i-1,j}+1\) 来更新 \(f_{i,\gcd(j,a[i])}\)
Gellyfish and Camellia Japonica
可以将答案构造出来以后,最后再正着模拟一遍看看有解还是无解。
就比如这道题,倒着推每一步都是基于存在解这个基本条件,每一步都走已知条件的必要条件,最后在正着模拟一遍就知道是否是存在解这个基础条件有误了。
// 这是份错误代码,无法正确判断是否有解
#include <bits/stdc++.h>
using namespace std;
int T,n,q,b[300010],lst[300010];
struct node{
int x,y,z;
} a[300010];
struct Gar{
int l,r;
};
vector<Gar> g[300010];
int ans[300010];
signed main(){
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
cin>>T;
while(T--){
cin>>n>>q;
for(int i=1;i<=n;i++) cin>>b[i],lst[i]=0;
for(int i=1;i<=q;i++) cin>>a[i].x>>a[i].y>>a[i].z,lst[a[i].z]=i;
for(int i=1;i<=n;i++){
if(lst[i]) g[i].push_back((Gar){0ll,1000000000ll});
else g[i].push_back((Gar){b[i],b[i]});
}
bool flag=true;
for(int i=1;i<=q;i++){
if(lst[a[i].z]==i){
g[a[i].x][g[a[i].x].size()-1].l=max(g[a[i].x][g[a[i].x].size()-1].l,b[a[i].z]);
g[a[i].y][g[a[i].y].size()-1].l=max(g[a[i].y][g[a[i].y].size()-1].l,b[a[i].z]);
}
g[a[i].z].push_back((Gar){min(g[a[i].x].back().l,g[a[i].y].back().l),min(g[a[i].x].back().r,g[a[i].y].back().r)}); //注意到 g 数组中 的 r 只在这里被更新以及使用——所以等于没用
}
for(int i=q;i>=1;i--){
Gar u=g[a[i].z].back();
g[a[i].z].pop_back();
if(lst[a[i].z]==i) continue;
g[a[i].x][g[a[i].x].size()-1].l=max(g[a[i].x][g[a[i].x].size()-1].l,u.l);
g[a[i].y][g[a[i].y].size()-1].l=max(g[a[i].y][g[a[i].y].size()-1].l,u.l);
}
for(int i=1;i<=n;i++) if(g[i].back().r<g[i].back().l) flag=false; //通过空区间来判无解是不优的,直接正着模拟是否符合条件即可
if(!flag) cout<<"-1";
else for(int i=1;i<=n;i++) cout<<g[i].back().l<<' ';
cout<<'\n';
}
return 0;
}
想想容斥(不要执着于全局容斥,想想部分容斥) 参考: CF1043F
巧妙利用异或的性质。
注意 \(s_i< t_i\) 保证了图是 DAG:于是应该直接考虑 DP,而不是贪心判定。
贪心匹配考虑调整法,观察调整后的答案是否具有某种特殊形式(交叉次数不超过 1 之类的)?
由于我们不关心达到最优情况的过程,只关心结果。于是我们可以选择一大步一大步的走——将想想如果信息被整合、打包起来,有什么快速的而不是模拟的方法计算出结果?这一步就可以用贪心了。
博弈题时注意当前局面的决策是否只和有限的值有关(遇到卡壳的地方可以考虑用贪心能不能想出结论来处理),可以考虑使用记忆化搜索。
#include <bits/stdc++.h>
using namespace std;
int T,n,a[110],cnt[100010];
double f[2][110][100010],g[110],h[100010];
map<pair<int,int>,bool> vis;
vector<int> fac[100010];
bool dfs(int g,int dep){
if(g==1) return 0;
if(vis.find(make_pair(g,dep))!=vis.end()) return vis[make_pair(g,dep)];
bool flag=0;
for(int i=1;i<=n;i++){
if(__gcd(g,a[i])!=g) flag|=dfs(__gcd(g,a[i]),dep+1);//gcd的好处就是快速判断哪些数没选过(没选过加上后gcd会变)
}
flag=(!flag);
if((cnt[g]-dep)&1) flag=0; //如果可以在gcd不变的情况选奇数个数,那么后手一定可以通过这个将必胜必败切换(通过贪心的结论处理暴搜索难以处理的部分)
vis[make_pair(g,dep)]=flag;
return flag;
}
signed main(){
// freopen("gcd.in","r",stdin);
// freopen("gcd.out","w",stdout);
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
cin>>T;
for(int i=1;i<=100000;i++){
for(int j=i;j<=100000;j+=i) fac[j].push_back(i);
}
while(T--){
vis.clear();
cin>>n;
int lim=0,gg=0;
for(int i=1;i<=n;i++) cin>>a[i],lim=max(lim,a[i]),g[i]=0.0,gg=__gcd(a[i],gg);
for(int i=0;i<=lim;i++) cnt[i]=0;
sort(a+1,a+1+n);
for(int i=1;i<=n;i++){
for(auto j:fac[a[i]]) cnt[j]++;
}
if(gg!=1){
if(n&1) printf("1 1.0000\n");
else printf("0 0.0000\n");
continue;
}
for(int i=0;i<=n;i++) for(int j=0;j<=lim;j++) f[0][i][j]=f[1][i][j]=0.0;
f[0][0][0]=1.0;
for(int i=1;i<=n;i++){
for(int j=0;j<=lim;j++) for(int k=0;k<i;k++) f[i&1][k][j]=f[(i-1)&1][k][j];
for(int j=0;j<=lim;j++){
if(j==1) continue;
int g=__gcd(j,a[i]);
for(int k=i-1;k>=0;k--){
f[i&1][k+1][g]+=1.0*f[(i-1)&1][k][j]*(k+1)/(n-k);
}
}
}
for(int k=0;k<n;k++){
for(int j=1;j<=lim;j++){
if(j==1) continue;
g[k+1]+=1.0*n*f[n&1][k][j]/(n-k);
}
}
for(int k=0;k<n;k++){
for(int j=2;j<=lim;j++){
for(int i=1;i<=n;i++){
if(__gcd(j,a[i])==1) continue;
g[k+1]-=1.0*f[n&1][k][j]/(n-k);
// if(k==1) cout<<j<<'\n';
}
}
// for(int i=2;i<=lim;i++){
// for(int j=i;j<=lim;j+=i){
// g[k+1]-=1.0*cnt[i]*f[n&1][k][j]/(n-k);
// if(k==1) cout<<cnt[i]<<' '<<i<<'\n';
// }
// }
}
int flag=0;
for(int i=1;i<=n;i++){
flag|=dfs(a[i],1);
}
printf("%d ",flag);
double ans=0.0;
// for(int i=1;i<=n;i++){printf("%.4f ",g[i]);}
for(int i=2;i<=n;i+=2){
ans+=g[i];
}
printf("%.4f\n",ans);
}
return 0;
}

多状态 dp 的时候考虑之后更新的数组会不会覆盖掉原来需要的数据(类似 01 背包)
遇见 gcd 相关问题的时候,可以考虑设一个数组 \(cnt_j\) ,表示 \(j\) 的倍数有多少个(即多少个数有 \(j\) 因子)
直接思考策略没有思路,可以考虑通过将小部分合并得到整体的方式,通过枚举子问题的合并得到大问题的答案。具体可以看看这道题的实现。
用两个 multiset 维护定长区间前 k 小。其中一个multiset存前 k 小,另一个存备用的。multiset 语法:删一个数:erase(it),如果 it 是指针则只删一个,若 it 是一个数则删除所有相同的数;访问 multiset 的最后一个元素: (--s.end()),是的要减减。
set RE 一般是对空的set进行了操作,仔细检查代码是否会导致某个 set 在不该为空的时候为空了。
写代码前一定要理清所有思路啊,若是思路只是在脑海中浮光掠影一遍,写代码的时候很容易就忘记要写某个部分导致检查很久检查不出来。就比如这题,备用 multiset 的作用不仅是当 前k小 不够的时候补充,还要考虑用备用 multiset 中更优的数 替换 前k小中的数(替换就说明两个set都要 insert 和 erase 一个数)
合并两个并查集,只需将两个并查集数组对应的 \(fa1_i,fa2_i\) 相合并即可。由此可以利用前后缀维护并查集信息。
多个数求 \(\operatorname{lcm}\) 是逐个 数相乘并除以他们之间的 \(\gcd\) ,而不是全部数一起相乘再除以 \(\gcd(a_1,a_2\cdots,a_n)^n\)
能不能有个清晰的想法时再来写代码?——尝试凝练,总结自己的想法,看看本质实在做什么?能不能更清晰的把性质表示出来?
CF346B Lucky Common Subsequence
处理字符串匹配相关问题时,匹配到前 \(i\) 个位置不一定是由匹配了前 \(i-1\) 个位置的情况转移过来,还要考虑 \(\operatorname{boder}\) 串的影响——考虑匹配了前 \(j\) 个字符,如果再加上一个,说不定就变成了匹配 \(i\) 个字符的情况。所以这种dp要考虑使用kmp。
调试的时候如果在程序某处修改了一个变量的意义,看一下其他用到这个变量的地方要不要改。
P7407 [JOI 2021 Final] 机器人 / Robot
考虑建一张新的图——我们的目标是找到最优解,而非使得新图可以完美无缺地体现出所有方案——我们可以使跑新图时出现一些不合法,但一定比最优解劣的方案,因为这些方案一定不会成为答案;我们不能始新图跑不出最优的答案,也不能使新图跑出比最优更优的答案。
可以发现,我们并不要求新图是原图的充要——找到性质,我们可以省略大部分的非必要细节,这样就能避免后效性了。
直接跑贡献会算重,那就建个虚点,多一条路作为正确答案。算重的我们不用再管,反正肯定比答案劣
棋差一招。凸包本质上是一个环,序列上的 DP 要考虑破环为链。
注意乘法的位置。如果两个维度的状态 \(x\) 和 \(y\) 在转移的时候只以 \(x+y\) 的形式,则可以将两个状态浓缩为 \(x+y\)。具体看我两次 ac 提交的差别。
多次询问考虑——数据结构维护,倍增,离线
这题其他两种方法都不好做考虑用数据结构维护。
Sol 1: 往一个合法的括号序列中任意两个位置插入一对已经匹配了的括号,则新的括号序列仍然合法。发现左括号一定在左边,右括号一定在右边,类似线段分治,考虑线段树维护左边区间可匹配的左括号数以及右边区间可匹配的右括号数。
Sol 2: 想不到线段树还想不到正难则反吗? 考虑删除最少的括号使得该区间的括号合法。依旧把括号序列转换为前缀和序列,要求前缀和序列的最小值 \(\ge 0\) 且最后一项为 \(0\)。我们并不关心怎么删,只在意删多少 ,显然直接对最小值和最后一项进行操作是最优的。预处理整个序列的前缀和,区间的就好求,区间最小值询用st 表解决就好。
分讨每种情况(不同的情况一定要分讨,不要想当然的直接归约到一类)的计数时一定要清晰,不要把某部分的贡献忘算了。转移数组的下标中出现了乘法,考虑调和级数优化。
单调队列处理区间的时候一定要记得边界要判断,不能越界。确保区间内的每个数都已经被尝试加到过队列里去。
状压 DP 的状态转移一般状态本身就蕴含阶段(总是从 1 的个数少的状态转移到 1 的个数多的状态),于是可以省掉一重枚举阶段的循环,直接枚举二进制状态。
同时,面对最优化问题,只要能确保不跑漏最优解,不跑出更优解,那么中间的转移只要能设计出状态,怎么写都是对的。
P2569 [SCOI2010] 股票交易
P2254 [NOI2005] 瑰丽华尔兹
单调队列维护的是一个可以以 \(l\) 和 \(r\) 的大小作为判定的决策点集合,并不一定要求是定长的区间,满足 \(l,r\) 均单调递增即可。
若当前点作为区间的右端点,我们可从小到大便利;若当前点为左端点,可从大到小遍历;若当前点为可选区间的中间点,可以把区间从当前点劈开,从大到小从小到大各进行一次遍历(P2569 题解实现)。
双指针的时候,r 表示右端点,处理的是区间的上界,不要被下界的限制条件干扰,导致上界无法拓展
细节一定要考虑清楚,特别是边界情况看看会不会出问题(算重啊之类的)……两个不同的错误拼在一起居然让我过了样例,警钟敲烂。
子序列型问题,由于 \(f_{i,j}\) 里其实包含了之前的很多状态(并非是强制以 \(i,j\) 为结尾的两个子序列),因此计数的时候直接加上 \(g_{i,j}\) 可能会算重,要简单容斥一下(计算当前贡献的时候,把之前的影响剔除掉)。
实现代码的时候要仔细,看看实现的某些细节是否实现到位,是否把想法中的某个部分漏掉了。
如果想要像求最长不降子序列那样子dp来做,需要保证选的数不会对后面的数有影响(如果影响可以只看最后选的那个数那就可以这么做),但是这题能选那些数还受已经选了多少个,以及以前选的数的影响故不能这么做。
原来是有个数组忘记放结构体里了,导致另一个数组排序后顺序变了而这一个没变
豪题。
for(int i=2;i<=1e6;i++){
if(!vis[i]) prime[++plen]=i,low[i]=i;
for(int j=1;j<=plen&&prime[j]*i<=1e6;j++){
vis[prime[j]*i]=1;
low[prime[j]*i]=prime[j]; //线性筛能找到最小质因子
if(i%prime[j]==0) break;
}
}
for(int i=1;i<n;i++){
int tmp=e[i].w;
while(tmp>1){
p[low[tmp]].push_back(i);
int now=low[tmp];
while(tmp>1&&low[tmp]==now) tmp/=low[tmp]; //注意这个步骤,实际上是在对多个相同的质因子去重
}
}
注意这段实现,我们先用线性筛找出每个数对应的最小质因子 low[i],然后利用这个 low 数组我们可以逐步得到每个数的所有质因子。总时间复杂度 \(O(V\log V)\)。
若关键点 or 边的总数很少,考虑建成一棵数量级和关键点数相同的虚树——考虑 dfn 排序维护最右链
P6902 [ICPC 2014 WF] Surveillance
倍增的本质,是通过一定的复杂度整合(预处理)信息,以达到高效回答询问的目的。
若是序列上的此问题,则做法为贪心。现在变成环,等价于处理 \(n\) 次序列上的询问:因此考虑利用倍增预处理,快速回答询问。考略将贪心过程中有用的量进行记录并dp。
想清楚算法细节再写,明确dp数组的定义,如果状态不合法的情况也要考虑。注意对于不合法状态的 dp 值特殊判断考虑
多细节dp要仔细考虑边界情况,有时候并不是一个判断就能解决的(比如这题,鸟飞到m就不会继续往上,因此当前的鸟若是在m位置,则可以从上一列的任何一个位置飞过来)。(注意题目这些特殊条件会带来什么影响)
P12684 【MX-J15-T4】叉叉学习魔法
P2149 [SDOI2009] Elaxia的路线
实现算法的时候一定要思考常数带来的影响!!!有时候 2 的常数就会导致 TLE(因为你的可能是非正解)。
这两题的共性就是都要求在最短路的基础上再处理某些限制。 对于这种问题我们可以考虑先对图跑最短路求出源点到每个点的 dis ,这些 dis 实际上对图进行了一个分层,使图变成了一个更容易处理的 DAG,可以考虑在这个新图上再解决原问题,以此来去除掉最短路的这个限制。因为在新图上每走一步都满足最短路的条件。
正解跟我的做法有点不一样,考虑化整为零,再化零为整。我们要求最短路上的最长公共路径,那么这条公共路径上的每条边一定同时位于两者的最短路上面——我们可以 \(O(m)\) 的判断每条边是否为公共边,于是得到了公共边集。公共路径一定是这公共边集中的一条链,且公共边集可以转为DAG,dp 跑最长链即可。
找性质:先考虑一个栈的情况——找到判定无解的方法,即 \(i,j\) 不能同时在栈中,需要两个栈。以此得到多个约束条件,将其二分图染色,也就是得到每个元素将要进哪个栈。然后贪心得到字典序最小方案(考虑当前操作对后面的影响,而不是只考虑前面的操作对当前的影响)。
dfs作差:考虑有一个全局桶,在dfs一棵树的过程中会不断被更新。那么遍历完点 u 的子树后,桶的增量就是子树内的贡献。前提是存储的信息支持作差。
用桶存东西时,可以推一下式子移一下项,可以使存的东西和查询更清晰。
构造题可以先尝试去掉一些限制,简化题意,构造出一个初始方案。然后找到一种调整方式,使得可以由初始方案得到所有方案,于是我们就可以调整这个方案,使得方案满足题目原本的性质。不要觉得构造题都很难,简化题意后的构造往往是简单的(比如这题如果不考虑数字的大小限制,可以先随便填三个数在一个矩形中,第四个数可以直接计算得出,对其他矩形也不影响),不要做复杂了。
要求构造一定范围内的解,可以考虑将题目转换后使用差分约束(有时需调整符号,使得变量满足查分约束的形式)。
P6033 [NOIP 2004 提高组] 合并果子 加强版
考虑每次操作的本质是什么:每次找出可能的合并后最小的果子。每次都找最小,故下一次合并肯定不会小于上一次(果子堆会不断变大),因此经过合并的果子具有单调性,这就是非常有用的性质。
upd: 说明一下为什么 经过至少一次合并的果子 具有单调性。考虑当前合成的果子堆大小为 \(A\),\(A\) 是由两个小果子堆合成的,即 \(A=a_1+a_2,a_1<a_2\);上一次合成的果子堆为 \(B\),\(B=b_1+b_2,b_1<b_2\)。若 \(a_1=B\),由于 \(a_2>0\) 因此 \(A>B\);若 \(a_2=B\),而又因为 \(a_1<a_2=B\) 因此显然不会用 \(b_1,b_2\) 来合成 \(B\),肯定会用 \(a_1\) ,与贪心策略不符;若 \(a_1,a_2\ne B\),那么按照贪心策略应有 \(b_1<b_2<a_1<a_2\),因此显然有 \(A<B\)。
综上所述,新合成的果子堆一定是单调的。
这题通常的做法应该是以 \(O(\log n)\) 的代价维护一段区间内的后缀最大值。但是我们发现每次往右移动一次右端点,那么右端点到前面某个定点的max是可以 \(O(n)\) 维护的——但这不是区间最大值,只是区间内某个定点右边的最大值——于是我们可以分讨最大值的位置,一次从左往右扫表示最大值在定点右侧,一次从右往左扫表示最大值在定点左侧。这样就考虑了最大值的所有位置且维护的复杂度是 \(O(n)\) 的。
如果觉得一种写法没前途(尝试新建一张图使得图上1~n的路径集合等于原图上长度不超过 T 的路径集合),要果断的用理性尝试叉掉。
将路径长度设为状态dp是行不通的,可以尝试将答案(经过的节点数)设进状态,将路径长度作为dp的值来辅助转移。问题转换,经过 j 个点的最短路径长度。注意到该题的特点是,所求答案比较小,而性质的数据范围非常大,因此可以把答案设入状态,将限制量放入 dp 值内,在转移的的时候通过 dp 值限制。
\(O(n^2\cdot2^n)\) -> \(O(n\cdot 2^n)\)
两份代码的差距仅在一个 break。好好体会一下这种思想。\(O(n^22^n)\) 的状压,以多花费 \(O(n)\) 的代价,使得我们可以求出在满足最优的条件下,所以的发射顺序;但是此题并不要求我们求出所有的这些顺序,因此我们可以自己钦定一种顺序——每次都打未被击中且编号最小的鸟(显然最优解可以通过调整顺序使得其满足我们钦定的情况),因此这样依然能够求出最优解的大小,并减少一重循环(即加上一个 break)。
卡常技巧:一个序列乘一个矩阵复杂度上限是 \(O(n^2)\) ,建议单独写一个函数实现,就没必要再用大常数的稀疏矩阵乘法了。
图上问题既可以考虑转为 DAG 后拓扑跑DP,也可以记忆化搜索。
性质往往能起到启发做法的作用。
思路要灵活转换:每个数最终能得到的贡献不好求,那么就求每个操作最终会做出的贡献。(Alexwei题解的思路非常自然)
正着做和倒着做,孰优孰劣要分析清楚。
考虑没有限制时是简单的,于是先处理总情况,再将不合法的情况减去。
upd:对于选取物品个数有 \(\le\) 限制计数,一般不好做,那么尝试将其容斥,转为对 \(\ge\) 的限制进行计数。由于选取的下界确定,我们可以钦定一部分是必选的,剩下的部分是任意选的。也就是说 \(\ge\) 会比 \(\le\) 更容易计数。
观察题目中是否有小量,可以考虑 \(O(2^n)\) 容斥。
CF1184E3 Daleks' Invasion (hard)
并查集缩边
适用于所枚举的非树边具有某种单调性,使得当前边所覆盖的树上路径不应受后面枚举到的非树边的影响,因此可以将边及时缩起来保证复杂度。
void merge(int x,int y){
int fx=find(x),fy=find(y);
if(fx==fy) return ;
if(dep[fx]<dep[fy]) swap(fx,fy); //并查集的代表元素总是当前集合中深度最小的节点
fa[fx]=fy;
}
void update(int x,int y,int w){
x=find(x),y=find(y);
while(x!=y){
if(dep[x]<dep[y]) swap(x,y);
ans[id[x]]=w;
merge(x,f[0][x]); //将 x 到父亲的这条边缩起来,这样以后就不会再便利了
x=find(x); //一次性跳到最上方的顶点
}
}
由于每次加边会改变树的形态,不好预处理出树的信息。我们可以把加完所有边的整颗树都建出来,这样就可以预处理了(因为之前加边过程中的树都是大树的子树)。然后就可以用并查集缩边了。
先筛出质数再用质因数得到因数个数,复杂度是 \(O(\dfrac{\sqrt M}{\ln M})\) ,可避免卡常。
可以利用 这题 的结论:任意整数满足 \(X\bmod M=(X\bmod A)\bmod M\),其充分条件是 \(A\) 是 \(M\) 的倍数。在这题的倍增做法种,我们既需要数组值 \(\bmod ~n\) 也需要 \(\bmod~ p\),按理来说要开两个数组分别记录。
但是拥有了结论之后,我们可以直接用 \(\bmod (n\times p)\),需要模 \(n\) 时再模回去,模 \(p\) 时同理。
T637555 R4 - T2 梦世界魔法详解(magic)
函数 or 循环 retun,continue,break 前一定要检查是否有一些必做操作没做完然后才能退出!!!
防止溢出,可以考虑我们所需要的值是否存在一个上界,超过这个上界的部分可以直接不管。
每次都删除一个序列中的一些数,每轮都要访问没被删除过的数字,这个过程可以用树状数组+倍增实现(可以随机访问第几个未被删除的数),或者使用并查集(只能查询第一个未被删除的数以及下一个未被删除的数)。
基环树换根。
代码实现细节较多且不显然的题一定要抚顺思路在写,最好可以把思路写在纸上清晰一点。
维护一个滑动窗口中间某个点的信息,可以以这个点为界将滑动窗口分为左右两半,分别以该点作为右端点和左端点进行扫描。
参考 兔队线段树 ,这种二次递归 or 倍增计算贡献的方法很妙。
统计方案时,考虑那些部分是相关的,要同步 dp 计算;那些状态是无关的,可直接分别计算再用乘法or加法原理合并。
方案数背包支持 \(O(V)\) 删除 or 增加单个物品,具体过程考虑容斥(f 表示原方案数组,f' 表示删除掉 w 的重量物品时的新数组):
计数题想出做法后不要盲目相信,要仔细考虑是否算漏,算重。像这题,我原本的思路就没有考虑到 分子与分母的一部分最大公因数会被抵消而形成的不循环分式,因此就算漏了。算重同时也不可忽略。
一定要识别清楚题目究竟是简单情况还是复杂情况:问题的本质究竟是树还是链,复杂度是否能被均摊?
考虑链与树再做法和性质上有什么区别(有什么情况,是树不好做但链好做的),考虑一个单独的区间与一个区间序列的区别(一个区间,是不是只有做右端点会移动?而一个区间序列是不是还要考虑断点?)
我自己的做法:由点与点的距离要小这个要求出发,考虑点对间的最大距离,也就是树的直径,从而发现一些性质
NOIP2016 天天爱跑步 P1600
考虑树上差分的想法:将链信息转换为子树信息(分别处理 s,t,lca(s,t),fa[lca(s,t)] 处的信息)。于是子树信息就可以考虑 dsu on tree (将表达式移项可将维护的东西变得更加清晰,即变量分离,每个节点只存仅和自己相关的信息)
同理 P4149 Race 也是类似,考虑通过每条路径的lca来刻画路径,那么也可用通过lca将路径变为子树内的问题(lca 与 lca 两条向下的链组成了路径),也可以 dsu on tree。该方法可行,是因为路径长度是可以 dep(u)-dep(lca) 得到的,满足可减性,故 lca 的子树内 u 到 lca 的距离可以只通过 dep(u)来刻画,即分离了变量,方便利用桶实现。
贪心:考虑覆盖还没被覆盖的最深的节点,一定选他的爷爷最优,不断进行这个过程即可。
在 dp 转移中可利用一些贪心的思想来优化冗余转移。比如这题,在足够的空余时间中多安排一辆车,肯定会比不安排更优,故可以优化转移下界。空车一定没好处:故有大量的发车时间,即状态是无用的:
省略无用状态,不一定要放弃枚举这个状态,也可以是这个无用状态可以快速于有用状态得出。
if(i>m&&sum[i]-sum[i-m-1]==0){
f[i]=f[i-m];
continue;
}
贪心不要盲目: 这里的贪心应该是 在车已经可用的情况下的空余时间 不能超过 m,所以一个人的最长等待时间是 2m ,而不是一有车就上,等待时间为 m。可以利用这个性质,将等待时间设进dp状态里。
另一个例子是 P2279 [HNOI2003] 消防局的设立 贪心应该是每次优先选还未被覆盖,深度最深的祖父,而不是盲目删点导致图不连通。
T647136 「假面愚者」 这题的修改之间相互独立,可以考虑使用 cdq 分治。
R13 C. 数据结构 这题修改之间会互相影响,并不独立,不考虑 CDQ。
由于此题要求对操作进行删改,维护原序列难以实现,于是考虑维护 操作序列 本身。此时就要想到,把原序列的初值改成一系列操作,此时整个问题只需要对操作序列进行维护即可。
考虑将删除转为倒序插入,这样子每次插入都是在总操作序列上不断点亮某个操作。灵感类似 T649737 R9 - B. 万物有灵

多测跑点双,一定要把 st 数组也清空,因为 top+1 可能会访问一些 n 以外的位置,如果没清空就有可能错。
计算根的儿子个数的时候,不要把返祖边也算上了,要放在 if 里面计算。
格路计数,别用网格图,用以 (0,0) 为原点的直角坐标系图。
核心是翻转反射。原问题是不经过某条线计算到终点 (n,m) 的方式,将终点关于线反射得到新终点。此时到新终点的任意路径都是原问题中经过该线的方式,容斥即可计算原问题答案。
资料
反射容斥
证明考虑组合意义,相当于在 A+B+1 个数中逐个枚举最大值。
AT_arc194_b [ARC194B] Minimum Cost Sort
错误思路:考虑两个数的移动之间共用了某个交换操作。这样子做针对某个操作以及某两个数,针对性太强,细节很难处理不好做。
正确:因该能发现在前面的交换是优于后面的,于是应该优先让前面的数现在前面交换好,后面再移动到后面去。具体就是,从前往后,依次交换保证每个前缀变得有序。另一种理解方式:假设位置 i 前面有 cnt[i] 个数大于 p[i],那么 p[i] 无论如何都至少要交换 cnt 次,才能让前面的数过去后面。这是一个下界,接着根据上述方法我们可以理解下界可以取到。因此一个贪心思路就完成了。
upd: 邻项交换题目考虑一下逆序对。显然一个数左边比他大的数最终一定要去到这个数的右边,也就是说这个数至少要进行 其逆序对个数 次左移操作,而进行这么多次左移操作的最小代价方案,一定是把当前数一直往左移,而不走回头路。因此我们找到了问题的一个下界,现在考虑这个下界是否可能取到,发现只要当前数前缀部分已经有序了,那么就可以保证加入这个数后前缀依然取到下界。于是整个序列的下界是可以取到的。
AT_arc196_a [ARC196A] Adjacent Delete
由于答案是求最大值,那么如果相减是负数那么一定不优,不会对答案产生影响。所以将绝对值看成减法,这样每个元素都会有一个正负属性,表示对答案的贡献。同时当 n 为偶数时,无论如何安排正负,都能得到一种符合题目限制的删数序列,因为总会有两个正负相邻,故只要选前 n/2 大的为正,后 n/2 小的负即可;当 n 为奇数时,有一个数无法被删除,这很严重,他会将左右两边分成两部分,互不相通。所以不能再像偶数情况那样直接赋正负,注意到剩下的那个数编号一定为奇数(左右两边因该分别都是偶数个数,否则还会剩下一些数,与只剩一个数不符),左右两边分别用偶数的方法处理即可。可以使用对顶堆,处理前缀 i/2 小。
upd: 由于我们的目的是,能取到最优解且不会取到不存在的更优解。秉着这个原则,我们发现绝对值是一个“无向”的减法,倘若我们对其定向,将绝对值拆成减法,负数不会影响最优解的存在,同时可以将贡献均摊到每个数上,这样子更好贪心 了。
AT_arc130_c [ARC130C] Digit Sum Minimization
贪心 + 模拟。
贪心需要找到某个性质,类似至少,或者越多越好之类的,并构造方法使其达到。这题中就是进位一定优,并且两数和越小越好。
范围较小的时候,难以贪心的部分可以直接枚举解决,比如这题中,第一对产生进位的位置是特殊的,比较不好贪心,所以直接枚举是哪两个数产生的进位。注意到确定了第一个进位后,高位上可以全部产生进位,不会使答案更劣,同时每个进位都是可以互相交换的,无关顺序,直接贪心随便取即可。
AT_arc164_c [ARC164C] Reversible Card Game
考虑 B 一定能将所有牌都拿完,故他至少能得到每张牌最小值的和。于是接下来可将牌的价值一面看成较大值和较小值的差值,一面看成是 0。显然 B 的目标就是取到 非 0 和尽量大的牌,A 则相反。考虑对局面进行一个总体的分析:若此时 A 面对的牌组均为 0,那 A 只能将一张牌翻为非 0,之后 B 一定会取走这张非 0 牌,从而回到全是 0 的局面。这提示我们局面貌似只与当前非 0 牌的数量有关,因此分析可知,只要出现了一次全为 0 的局面, B 就能拿完所有的非 0 牌;假设 A 面对的局面是场上至少有一张非 0 牌,那么翻 0 牌肯定不优,因为这说明最大的那张 非 0 牌一定会被 B 拿走且最终非 0 牌总数没变,A 面对的局面没有变化。因此 A 一定会翻最大的那张非 0 牌让他变成 0。此时若场上还有 非 0 牌,则 B 取走最大的一定优,因为取哪张牌不会对接下来的局面产生更劣的影响。若场上均为 0 牌,则 B 应该选一张面值最小的拿走,损失最小化。
接下来只需要用两个堆模拟这个过程即可。
dp 的核心是对问题进行抽象,找到用少量状态刻画原问题的方式并进行转移。
按常规的对区间进行排序并从左到右贪心维护一个堆,确实可以得到最少要用多少个乐队,但是这个动态的思路对 dp 的适配性太差。我们尝试寻找新的刻画方式:设时间点 i 被区间覆盖了 \(t_i\) 次,那么 \(\max(t_i)\) 就是至少需要的乐队数。同时发现由于没有重复区间,那么 ti 相对于 t[i-1] 的变化量一定小于等于 1,容易从 t[i-1] 考虑 t[i],于是就启发我们对 t 序列直接 dp。
现在问题转换为,已有一个合法的 t 序列,如何求出有多少种区间集合可以达到这个 t 序列。
考虑我们已经知道了对应 1~i-1 的 t 序列能有多少种区间集合,那么现在把 ti 纳入考虑:若 ti=t[i-1]+1 ,那么覆盖 i-1 的所有区间,必须同时覆盖到 i 一个都不能断(如果断了,说明在 i 这个点至少有两个新区间,这与区间互不包含不符),同时还得新增一个新区间的左端点在 i,因此产生一倍的贡献;若 ti=t[i-1]-1 ,同理,则覆盖 i-1 的区间中,必须是左端点最小的那个区间断掉不覆盖 i,其他区间照样延伸过来,产生一倍的贡献;当 ti=t[i-1] 时,既可以选择断 i-1 并产生一个新区间在 i,也可以选择原封不动地继承 i-1 的所有区间,故一共有两倍的贡献。
这种一位一位考虑贡献的来源,就是计数 dp。
由于最后剩下的数的个数一定小于 k 个,故可以考虑把终态设计成状态,2^k。
一开始我想着 f[i][j] 表示经过若干次操作 i 这个前缀变成状态为 j 的终态时的答案,但后来可以发现前缀这个东西在这题中是意义不大的,不好转移。
考虑将剩下的数还原展开,他们一定各自对应了一段原序列中的区间(区间长度不一定是 k ,因为可以是一段很长的区间经过多次合并得到了一个数),且这些区间相邻但不相交。说明这些区间间是没有互相影响的,在最优解中,是不会有同时跨越两个这些区间的操作的。对于这种由可划分区间组成最优解的问题,可以考虑区间 dp。
设 f[l][r][j] 表示对 l~r 进行若干次操作得到终态为 j 的答案。我们套路地考虑用两个小区间合并出 [l,r],但是我们有必要枚举左边区间的终态 p ,右边区间的终态 q 吗?首先根据上面的分析,我们知道一大段区间的结果可以由若干段牵连的区间合并而来,因此我们是没有必要再对 p,q的合并进行额外的合并,因为我们钦定这两个区间是划分开的。其次,我们其实也没必要枚举 p 和 q,因为这样子枚举的太细,会在不同的区间分割点处处理重复的情况。我们实际上只需要保证右边的小区间只合并出一个数字,左边的区间合并出剩下的数据即可,容易发现这样子枚举依然能覆盖所有的合法可能。即左边的区间终态是 j>>1,右边的终态是 j&1。
upd: 相当于我们枚举的是最右边的的树,最终会扩展成哪个区间。
当然,当终态的数字个数为 1 的时候,利用上面小区间合并的时候就要额外处理一下,要先合并出 k 个数,然后再用一次合并把这些数合并为 1 个数。
upd:枚举区间断点进行合并的时候,要保证断点左右的区间合并后会产生本质的不同。就比如说括号序列,(())()(),用 (()) 和 ()() 合并与用 (())() 和 () 合并就没有本质不同。如果不满足的话,我们就得钦定左边的区间只能是这种 (...) 的形式,要额外设计状态 dp 预处理一下。类似 P7914 [CSP-S 2021] 括号序列

如果没有总段数最少这个限制的话,这题直接 dp 加优化即可。但是加上了限制后,每段的划分就会变得没那么灵活,尝试考虑该限制是否具有子结构性:即若整个长度为 n 的序列的分段满足限制,那其前缀 i 的分段是否满足性质?由于原序列的最优段数为 $\left \lceil \frac{n}{k} \right \rceil $,前缀 i 的最优段数为 \(\left\lceil\frac{i}{k}\right\rceil\),满足不等式 \(\left\lceil\frac{i}{k}\right\rceil+\left\lceil\frac{n-i}{k}\right\rceil\le\left\lceil\frac{n}{k}\right\rceil+1\)。因此我们发现若前缀 i 的所分的段数不是最优段数,大于了 \(\left\lceil\frac{i}{k}\right\rceil\),那么后面无论如何怎么分整个序列的段数一定会大于 \(\left\lceil\frac{n}{k}\right\rceil\),不合法。故任意一个前缀也必须满足最优分段,因此此问题具有最优子结构,可以利用线性的 dp 状态解决。
设 f[i] 表示前缀 i 的答案,转移就是 f[i]=max(f[j]+maxn),其中 j 要满足 \(\left\lceil\frac{j}{k}\right\rceil+1\le \left\lceil\frac{i}{k}\right\rceil\)。经过数学推导可知 j 的范围就是 \([i-k,k\times(\left\lceil\frac{i}{k}\right\rceil-1)]\)。然后由于还要维护一个后缀最大值一样的序列,可以考虑用线段树维护,需要线段树二分以及区间覆盖操作。
实现细节: a[i] 的值是纳入 f[i] 的计算当中的,所以
a[i] 的值是纳入 f[i] 的计算当中的,所以 update1 一定要放在 f[i] 的更新前面。
同时,注意到 f[i] 的转移是 f[j]+ \(\in[j+1,i]这段的最大值\) ,也就是说 f[j] 的转移是不包含 a[j] 的。但是我们维护的线段树是一一对应 a 序列的,因此算上 f[j] 的还得向右平移一位,也就是 +1。同理,查询的区间也都要补一个 +1。
线性做法:考虑 dp 的转移,是 \(j\in[i-k,k\left\lceil\frac{i}{k}\right\rceil-k]\) 转移到 i 的。如果我们把原序列按照长度为 k 分块,那么每一块的 i 都是由上一块的 j 转移过来的。虽然转移时有一个最大值的操作横跨了当前与上一个一共两个块,但是一个经典的技巧就是 对最大值进行分类讨论,实现分离变量(T647135 「不可知域」)。我们分讨最大值的位置,如果位于上一个块,那么转移的信息就只和上一个块有关,与当前的 i 无关,完全可以预处理出来;如果位于当前块,那么转移时我们只需要选上一块 f[j] 最大的即可,在加上当前块的前缀最大值,此时也实现了上一块与当前块的分离,可以预处理。

分讨最大值,实际上是对最终的决策点(对答案有贡献的那部分)进行分讨,讨论他到底是从哪来的,这样就能通过分讨分离变量,把他的可能范围变得更好处理。
必须要在基环树上断掉一条边,但是我们不能枚举到底断掉哪一条。
手玩一下样例2的数据,可以发现断掉一条边相当于一次反悔操作,使得可以不走下一个环上的点,而是走之前走过的环上的点的其他分支。因为要求字典序最小,所以越早反悔越好,只要遇到走之前的分支由于走到下一个环点,那就不走这个环点,留给另一边走,代码简单实现一下这个过程即可。
代码一定要静态查错 一次,避免出现 v 写成了 u 之类的错误。
无向图基环树找环,一定要一找到就退出遍历,否则环会被访问两次!

ps:拓扑序比拓扑层数更强一点,拓扑序是每个点有唯一编号的,是互不相同的;而相同的拓扑层可能有多个点。
考虑 DAG 上的一条路径,路径上的点按移动顺序排列,一定是拓扑序升序的。这就说明,如果一个点 x 的拓扑序大于某条路径起点的拓扑序,并小于该路径终点的拓扑序,那么该路径上必定存在一条边 (u,v) 满足 top[u]\(\le\)top[x]\(\le\)top[v]。利用这个性质,我们可以方便的判断删除点 x 后,图中还存在哪些路径。显然只要一条路径不经过 x,那么操作后会被保留。而由于上述的性质,一条路径不经过 x,当且仅当,其起点的拓扑序大于 x 的拓扑序或其终点的拓扑序小于 x 的拓扑序,又或者路径中存在一条边 (u,v) 使得 top[u]\(<\)top[x]\(<\)top[v]。有了这一部思考,我们就可以很方便地找出删除 x 后图中的最长路。
设 diss[u] 表示以 u 为起点的最长路长度,dist[u] 表示以 u 为终点的最长路长度。枚举每条边 (u,v) ,显然 dist[u]+1+diss[v] 就是经过边 (u,v) 的最长路,这条路径显然一定不会经过拓扑序在 (top[u],top[v]) 范围内的所有点,在线段树上对这些点进行更新即可。然后考虑删除点 x 后图上的最长路就是在线段树上进行一次单点查询,在与所有拓扑序编号小于 x 的 y 的 dist[y],以及所有拓扑序编号大于 x 的 y 的diss[y] 进行比较即可。
法2。
考虑我们每删除一个点 x,点集就会被分成拓扑序小于 x 拓扑序的点 S 以及大于 x 的点 T,一共两个集合。显然由于 DAG 的性质只有 S 中的点会向 T 中连边,我们称这种跨集合的边为特殊边 (u,v)。考虑操作后图中的最长路,只可能是 S 中的点 y 的 dist[y] 的最大值,或者 T 中的点 z 的 diss[z] 的最大值,或者所有特殊边 (u,v) dist[u]+1+diss[v] 的最大值。如果我们按照拓扑序从小到大的顺序来枚举删除的点,那么每次都只会有一个点从 T 集合移动到 S 集合,特殊边集会减少入度条边并增加出度条边,这个总变化量是 O(n+m)的!于是我们可以想到用三个 multiset 维护 S,T,以及特殊边集三个集合,单次更新的复杂度为 log,整个算法的复杂度就是 nlogn 的了。
沿用 P3573 [POI 2014] RAJ-Rally 的思路,我们可以尝试枚举路径,看看它没有经过哪些边,那这些边被删后就不会对这条路径产生影响,于是可以用这条路径更新这些边。P3573 [POI 2014] RAJ-Rally 中,由于 DAG 上的点自带一个拓扑序,以及路径拓扑单调的性质,这些不被某条路径经过的点构成了区间,可以用线段树维护这些点的答案。但是由于本题是无向图,哪怕可以通过只走最短路上的边将图转为 DAG,但还是任然不对。因为不经过某条路径的边这个东西,本身没有像“形成一段区间”这样这么良好的性质。
容易注意到,我们找出图中 1 到 n 的任意一条最短路,那么最终删除的边一定是在这条最短路径上的。所以我们枚举其他路径的时候,其实只需要关心他不经过这条最短路中的哪些边即可,其他可以不管。
此时还有一个性质:由于仅在图中删除一条边,那么操作后图中 1 到 n 的新最短路,至多只会经过一条,不在原图的最短路生成图 DAG 中的边。也就是说至多只有一条边是 DAG 中没有的,其余都是原本 DAG 中的边。因为,如果新的最短路中存在一条不在 DAG 中的新边,那么说明原本连接边两端点的最短路中有条边被删了,得找替代。也就是说其他部分的边都不会被删,因此最多只需要一个替代,即至多只有一条不在 DAG 中的新边。
因此,其实也没必要枚举路径,我们可以只关注原本 DAG 之外的那条边是那一条。枚举边 (u,v),不管他是否是原本 DAG 中的边,从 1 到 u 以及从 v 到 n 都只能走原图中的最短路,那么这条新路径的长度就是 dist[u]+w+diss[v]。由于“从 1 到 u 以及从 v 到 n 都只能走原图中的最短路”这个性质,除边 (u,v) 外的部分其实都是已知的,可以预处理的。
考虑强制经过这条边的从 1 到 n 的最短路,会绕过原本最短路上的哪些边。容易发现绕过的这些边一定构成一个区间!那么就可以用线段树进行维护了。至于绕过哪些边这个东西,可以在 dij 的过程中找到每个点的前驱,然后整张图就变成了一个最短路径树(注意最短路径树只包含一条最短路,而最短路生成的DAG有向图包含所有最短路,强制便利图的话复杂度会假),然后遍历一遍即可预处理出来。
upd:在图中删除某种元素 A,考虑枚举图中的另一种元素 B,用 B 的贡献来更新与 B 无关的 A 的答案,需要找到 B 与 A 的关系(合法的 A 构成一段区间之类的),使得这种更新方式可以在可接受的复杂度内实现。
维护答案集合内每个元素的值,最后再求解答案。类似于维护每个操作的贡献。
dp 需要将问题划分为多个互不相交的子问题进行转移。
一开始的错误的思路:考虑计算 \([l,r]\) 内的答案,显然 r 处一定要放一个监察员。考虑求出从 r 向左看,第一个会被挡住的位置 k,那么 k 要么上面有检查员,要么 k+1 上有检察员。所以 f[l][r]=min(f[l][r+1],f[l][r])+1 。但这个思路是错的,因为 \([l,k]\) 内还会有可以被 r 看到的点,他们实际上不会使答案更劣,但是 f[l][k+1] 这个dp状态的定义却没有考虑到后面 r 的影响。因此,实际上用这个式子计算的答案会偏大。
上面思路的问题在于,我们分割子问题的方式是不对的,前后两部分子问题有交,会互相影响。
假设 \(a<b<c\) 三个位置分别都能在 r 处被看到,\(x\in(b,c),y\in(a,b)\)。显然,此时有 \(h_x<h_c,h_y<h_b\) 否则 \(x\) 或者 \(y\) 就会被 r 看到。如果 \(x\) 能够看到 \(y\) ,那就说明 x 与 y 连线的斜率比 x 向 x,y 之间任意一点连线的斜率都要小(可以画图理解),但是 x 真的看得到 y 吗?实际上,x 是一定看不到 y 的,可以画图理解。因此,序列就被 r 能看到的点分割成了多个与 r 无关,且互不影响的区间。
此时可以考虑区间 dp ,设 f[l][r] 表示区间 [l,r] 的答案。我们固定 r,从右往左枚举 l。假设 r 在该区间中能看到的最靠左的点为 p,则 p 右边的区间与 p 左边的区间已经无关了,相互独立。且我们要么在 p-1 监视 p-1,要么在 p 监视 p-1。因此 f[l][r]=min(f[l][p-1],f[l][p])+num 。其中 num 表示 p 右边区间的贡献,我们要在枚举 l 的时候顺便维护这东西:当 l 能被 r 看见时,此时就要用 num+min(f[l+1][p],f[l+1][p-1]) 更新 num,并用 l 更新 p。
解整数不等式,一定要利用 ceil 和 floor ,否则要判断很多正负。
\(ax+b>c,a>0\) 时,\(x\ge\) floor((double)(1.0*(c-b)/a))+1
\(ax+b>c,a<0\) 时,\(x\le\) ceil((double)(1.0*(c-b)/a))-1
我的做法:将物品的重量按照 \(a\times 2^b\) 的 \(b\) 分成 \(b>10\) 和 \(b\le 10\) 两组。对于 \(b<10\) 的那组,物品总重量最大为 \(2^{10}\times n\times a\),是 \(10^6\) 级别的;而 \(b>10\) 的那组,由于每个物品的 \(w\) 都是 \(2^{11}\) 的倍数,因此我们可以每个都除去 \(2^{11}\) ,同时背包最大容量 \(W\) 也应该除去 \(2^{11}\),所以这时候背包的容量也降到了 \(10^6\) 级别的了。两次分别 dp 再枚举合并即可。
sol: 未完待续……
一开始就往 dp 去想了,赛后才发现只要把题意稍微抽象一下,就能发现是一个简单数学题。
考虑操作序列本身的特点,一定是一个复制操作,后面跟一连串粘贴操作。我们其实没必要关心每次粘贴时剪贴板里到底存了什么长度,因为如果称由一个复制开头,若干个粘贴结尾的操作子区间视为一个整体,长度为 a[i],那么操作序列就是由至多 logn 段这样的区间连接而成,且最终字符串的长度为 \(\prod\limits_{i=1}^ka_i\)。于是我们就将此题转为了一个乘法问题。考虑枚举 k,也就是复制操作的使用次数,那么只要 \(\sum\limits_{i}^ka_i\) 固定,那么总操作时间显然也固定了(因为粘贴操逇总数不会变),此时要让乘积尽量大,那就是均值不等式,让 a[i] 尽量平均即可。

大整数乘法先除再乘防止爆 ll。
ps: 赛时的 dp 做法是设 \(f_{i,j}\) 表示凑出长度恰好为 \(i\) ,最后剪贴版内长度为 j 的最少时间。发现 \(f_{i,j}\) 一定是从 \(f_{j,j}\) 经过若干次粘贴操作转移过来,因此一定有 \(i\equiv 0\pmod j\) 。这时候就会发现 dp 的第二维其实没什么用,我们直接改成 \(f_i\) 表示凑出恰好长度为 i,且最后进行了一次复制操作的最小时间。那么 i 就可以通过他的因数 d 来转移,容易做到 \(O(n\log n)\)。
这时候如果进一步,就能发现正解的性质:我们先找了 i 的因数 d 来转移,而 d 又是由其因数 d' 来转移的……,每一步转移的代价都可以归约为形如 \(\frac{i}{d},\frac{d}{d'},\cdots\) 之类的东西!发现这些东西相乘的乘积是固定的,都是 i,而贡献则是全部加起来。因此转为一个乘积固定,让和最小的问题,可以考虑均值不等式。
经典 trick:求凑出某长度的最小时间,不妨求某时间能凑出的最长长度。而在这题中,最长长度是没必要知道的,我们只需要知道是否大于 n 即可,这又节省了一个变量的维度。
由于后面的覆盖会影响前面,不好处理,于是可以把整个过程倒过来,从后往前倒过来做,这样“后”操作的就不会影响到前面的序列。由于每次覆盖都是由上一次的终点开始平移一段距离,因此整个过程中的有色部分,一定形成一段完整的区间,且后面的操作不会影响前面,于是可以考虑区间 dp。但是如果不再增加一些限制,即使有色部分是一个区间,但是我们操作后刷子停止的那个点,可以是区间内的任何位置,这不利于我们进行转移。于是我们考虑整个有色部分的最后一次有效染色,即被成功染上的最小的颜色。显然最小颜色的位置确定了,该有色部分的其他地方都不会被改变了。而且,若我们保证最后一次染色操作是有效的,那么刷子一定会停在有色区间的左右端点中的一个上,这就可以转移了。
设 f[i][l][r][0/1] 表示进行了后 i 次操作后,最后一次有效染色的颜色为 i,最后停在左/右端点,的不同颜色序列的种数。我们考虑用 f[i][l][r][0/1] 来更新 f[k][l][x][1] 以及 f[k][x][r][0],其中 k<i,表示我们从 [l,r] 区间中,通过染 k 这种颜色将有色区间往左或往右延伸了一部分。那么是否所有的 (k,x,0/1) 都合法呢?显然我们既然钦定了 k 是继 i 后第一次有效染色,那么也就是说 [i+1,k-1] 区间内的所有染色都是无效,我们要保证这段区间内的所有操作能通过一系列平移,一直待在已有色部分内,而不会超出去成为新的有效染色操作。
因此,我们要另外维护一个 dp 数组 g[k][j],表示通过 [i+1,k] 这些操作,是否可以在保证每次移动在 [1,r-l+1] 范围内的情况下,最终停止于 j 处。有了这个数组,我们就可以知道 f[i][l][r][0/1] 是否能转移给 f[k][x][r][0],我们只需要查询 g[k-1] 中的某个值是否为 1 即可。
需要注意一个特别恶心的细节:当 i=n 时,即我们只进行了一次染色的时候,无论是从左端点还是右端点转移到同一边(比如从左端点往左延伸,或从右端点往左延伸),效果都是一样的(因为颜色只有一种,左右没有区别)。此时要注意特判,不能算重。
此时还是不能通过这题,因为直接转移是五次方的,我们考虑对状态进行优化。显然左右端点是镜像对称的关系,dp 值都是一样的,因此 0/1 这维可以省略。其次,我们每次操作其实并不关心左右端点的具体位置,其实只有有色部分的长度比较重要,我们可以直接将它写进状态里,就变成了 f[i][len]。最后统计答案的时候再乘上一个 (m-len+1) 表示平移即可,复杂度降为四次方。
诈骗题:定义一个区间其内最大值等于区间长度为好区间,则对于任意序列,好区间的数量是 \(n\log n\) 级别的。
证明考虑最值分治:最开始区间为 [1,n],考虑找到该范围内的一个最大值,计算包含这个最大值且长度为该值的区间至多有多少个。显然若最大值的位置为 p,则其贡献的区间至多有 \(\min(p-l+1,r-p+1)\) 个,就是其左右两边区间长度的较小值。然后再分治到左右两边去,即可计算其他区间。类似dsu on tree的证明,我们不考虑区间长度的总和这个复杂的玩意,我们考虑一个单点至多会对答案贡献多少次。显然若一个点要贡献一次,那么其所在区间的长度会翻倍,因此一个点至多 \(\log n\) 次。故最终区间的总个数至多 \(n\log n\)。
其实这道题有点诈骗:首先随机生成的数的范围只有 \(2^{24}\),提示我们应在值域上进行维护。可以在值域上建一个桶,桶的每个节点类似一个栈,不断的压入数的编号。这样就能保证栈顶的元素是被影响最晚的点。对于删除操作,我们可以用懒删除——s删除某个编号的数时,对该编号打上标记,当该编号被作为最小值被访问到的时候我们才删除(其实就是弹出栈顶)。这样子插入和删除操作都是均摊 \(O(1)\) 的。
最小值的操作按理来说比较难维护,但注意到我们不需要支持随机往堆里插入元素,而仅是将最小值删除后再插入,这等价于在值域上移动原本是最小值的那个元素的位置。我们可以在值域上维护一个扫描线 p ,表示 p 的左边(就是等于 p 或小于 p)只有最小值 minn 这一个元素。显然当初始化插入的时候,p=minn。当删除最小值并插入时(注意到这等价于值域上的平移),若新值 tmp<p ,则 p 仍然符合条件不变,minn 更新为 tmp;否则 p 需要更新,将 p 向右移动直到遇见第一个有元素的位置,更新 minn 为该值。此过程中,p 一直在值域上向右移动,所以均摊是线性的。
懒标记在对桶中元素进行修改后要及时下放,因为最小值随时都有可能被访问到,要及时更新。
虽然这个桶的操作很适合用 vector 来做,但是一次开 1e7 个vector容易爆空间,而且速度也很慢。考虑类似图论中,邻接表可以用链式前向星替代,此题中我们也可以采用类似链式前向星的写法。
选出最少的集合使得元素互不相交(序列选区间,树上选路径),可以考虑单点被覆盖次数的最大值。T645364 R7C - AVE
考虑如何判断树上两条路径是否有交:若一条路径的 lca 在另一条路径上,那么这两条路径有交,否则无交。手玩一下容易发现这是正确的。而这个性质启发我们,路径是否相交,可以用 lca 来刻画。
如果树上被链覆盖次数最多的点,被覆盖次数为 \(cnt\) ,那么划分集合的数量至少是 \(cnt\)。那么是否能取到这个最小值呢?我们尝试构造。考虑将被覆盖次数为 cnt 的所有点拎出来作为关键点,我们尝试选出一个链的集合,使得删掉这集合中的链可以使得树上的点被覆盖次数的最大值降为 \(cnt-1\)。如果能这样一直操作下去,我们就构造出了一组方案。
由于路径的相交与lca有关,而要是有交,一定存在链 a 的 lca 在链 b 的 lca' 的子树内。因此,如果我们每次选出dfs 序最小的,被覆盖次数恰好为 cnt 的那个点,那么由于 dfs 序最小,它一定不会被其“上方”的某条链覆盖。此时我们若能找出以这个点为 lca的一条路径,就可以将它放进集合中,不会与集合之前的链相交。而这条路径是一定存在的,因为若没有任何路径的 lca 为这个点,那么说明这个点的父亲一定也会至少被覆盖 cnt 次,这与这个点是 dfs 序最小的这个条件不符。
所以,我们每次在树上找出覆盖数最大,且 dfs序最小的点,选出一条以它作为lca 的链,将链删除(即将路径上的点覆盖次数减一),然后再进行下一轮,直到树上覆盖数最大的点变小,这样我们就选出了一个集合,集合总数达到了下界。
树剖维护即可。

选择 dfs 序最小的点,是为了保证其不存在其他关键点祖先。
upd:实际上找出关键点后,貌似任选一条覆盖其的路径即可(?),但是直接预处理出每个点上有哪些路径是苦难的,此时我们应该精简我们的可选集合:发现关键点 一定 具有一条 lca 在其上的路径,我们只需要利用它即可。这个是容易维护的。
考虑判断无解:若存在一个时间点 t,使得在 t 及其之前领饮料的人数大于 t,那么则无解,因为生产不过来。
因为只有 n 个人,所以一定是生产 n 杯饮料。如果考虑每个时间点产生体积为多少的饮料,有点不好做,我们转而考虑每个人拿到的是体积为多少的饮料。由于多个人可能要在同一个时间点拿饮料,那么就必须让一些饮料提前准备。显然如果某杯饮料要提前准备,应该尽量晚准备最好,这样就不会影响前面的饮料准备。考虑一个人 i 至少领到体积为多少的饮料:若 i 后面还有人的饮料被提前到了 i 之前准备,假设体积为 x,那么 i 领到的饮料体积至少得是 x 。显然下界是可以通过合理的构造取到的。
由于每个人能领到的饮料体积都受到其后面的人的已经准备好的饮料影响,自然能想到倒过来做比较方便,从 n 做到 1。于是我们可以考虑维护一个序列,里面存着应该提前准备,但还未准备的饮料体积(显然不一定只准备一个饮料)。第 i 个人至少领到当前这个序列中最大值的饮料,并将这个人将领到的饮料体积放入序列中(因为这个人的饮料也要准备,且未准备)。由于我们要将未准备的饮料尽量晚准备(由于我们已经倒过来了,所以在程序中是尽量“早”),所以我们一找到空余时间就要将序列中较大的那几个准备掉,也就是删除掉。具体的,每枚举一个顾客 i,就有 t[i]-t[i-1] 的时间可以用来准备饮料。
发现加入序列中的数单调不降,因此可以用一个栈来维护。
树上,如果 u,v 的路径中不存在割边,则在同一个边双。每加入一条非树边,都会删除掉一条链的割边。
显然可以将加边时间作为边权,建一颗最小生成树出来,这样只有非树边的添加会形成新的边双。对于每对(u,v) ,其树上路径上的所有边原本都是割边,而增加一条非树边 (x,y),会使 (x,y) 路径上的所有边都变成不是割边,可以理解为这条边被“删除”,删除时间就是添加这条非树边的时间。那么对于每个询问 (u,v) ,我们查询其树上路径中,最晚被删除的那条割边的删除时间即可。容易发现,当我们倒叙加非树边,这一系列操作就可以用树上链覆盖,和链查询最大值来完成。
sol2: T649737 R9 - B. 万物有灵 利用并查集缩边,我们可以按顺序找出每个时刻的边双。但我们还有询问要处理,因此我们可以把一个询问 (u,v) 分别挂在 u 和 v 所在的边双上。合并两个边双的时候就启发式的,便利询问数较少的那个边双的询问来处理,这样子合并的复杂度是 logn 的。code
P10680 [COTS 2024] 双双决斗 Dvoboj
根号平衡:找到题目中的两个量成反比例关系,或者说两种操作复杂度相差很大,那么考虑利用反比例关系来平衡。
\(|a-b|\) 这个东西显然没什么特殊性质可以维护,那么容易想到直接用 st 表做。但是单点修改就是 \(O(n)\) 的了(考虑修改一个点 x,那么对于长度为 \(2^k\) 的区间,总共有 \(2^k\) 个会因此受到影响。所以受影响的区间总数是 \(O(n)\) 的)。 注意到我们查询的复杂度是 \(O(1)\) 的,太快了,于是可以想到跟修改操作二者平衡一下——根号平衡。发现我们修改的问题在于,由于我们在 st 表中记录了很多很长的区间的答案,导致我们单调修改的时候,会对很多这样的区间产生影响。我们考虑让 st 表存的区间都短一点,比如长度不超过 \(\sqrt n\)。那么单点修改的时候,就一共只会影响 \(O(\sqrt n)\) 个这样的区间;而如果查询一个小区间,我们直接用 st 表存的答案即可,如果查询一个大区间,那么这个区间中至多包含 \(O(\sqrt n)\) 个我们上述钦定的小区间,且小区间内部的答案互不影响,因此问题规模缩小为 \(O(\sqrt n)\) ,暴力处理回答查询即可。
容易发现如果一个数前面有比他小的,那就能删。但是要注意,答案并非 \(2^k\),因为如果有多个相同的数字可以删,那么删除相同数量的所有选取方案都是等价,只能算一种。
P13687 【MX-X16-T5】「DLESS-3」XOR and Rockets
猜结论前要严谨思考,否则可能会像T664701 R14 - T2 复制粘贴一样得出假结论,影响做题效率。
如果 \(a_n\) 不操作,那么每次修改的 \(y\in [0,2^{13}]\),不太好让贪心发挥作用;如果 \(a_n\) 被操作过了,那显然越大越好,此时 \(y\) 就没有限制了,可以考虑贪心看看新的题目有什么性质。
显然每个数只会被操作一次,且操作顺序不重要。容易想到一个复杂度与值域有关的做法:考虑从后往前 dp,设 \(f_{i,j}\) 表示从 \(i\) 到 \(n\) 的数都已确定,其中第 \(i\) 个数为 \(j\) 的最小操作代价。由于 \(i+1\) 到 \(n\) 的操作对 \(i\) 的影响容易通过异或得到,可以实现转移 \(f_{i,j}=\max(f_{i+1,a_i\oplus a_{i+1}\oplus j},f_{i+1,k}+b_i),k\ge j\)。
一开始口胡错结论了,以为一定存在最优解使得每个元素不大于 \(2^{13}\)。但很遗憾,本题中,操作后的 a 序列最大值不一定小于 \(2^{13}\),需要分类讨论。
\(a_n\) 最后一定作为序列的最大值。如果 \(a_n\) 没被操作过,那么所有元素最终都一定小于 \(2^{13}\),可以用上述 dp 解决。现在讨论强制操作 \(a_n\) 的情况。假设最终操作了的位置构成 \(p_1,p_2\cdots p_m\) ,其中 \(p_m=n\),那么我们显然可以贪心的让 \(a_n\) 异或上一个很大的数,这样答案不会更劣。此时考虑倒数第二次操作,即 \(p_{m-1}\),无论它到底在哪,我们总能找到一个数,使得 \(a_{p_{m-1}}\) 异或完之后, \(p_{m-1}\) 前面的数无论接下来怎么操作都不会超过 \(p_{m+1}\) 后面的数,且可以通过对低位的异或调整内部的大小关系。 操作就是这么自由。通过这个性质我们可以发现,如果只看低位,那么 \(a_{p_{m-1}}\) 可以从任何大小的 \(a_{p_{m-1}-1}\) 转移,因为一定有办法通过操作,使得前者小于后者。
所以,对于强制对 \(n\) 进行操作的 dp 就是:\(f_{i,j}=\max(f_{i+1,a_i\oplus a_{i+1}\oplus j},f_{i+1,k}+b_i),k\in [1,2^{13}]\) ,只有 k 的范围发生了变化。
dp 的转移中往往要融入贪心得到的性质。
sol2: 依然考虑强制对 \(a_n\) 进行操作。由于每次操作都是一个前缀异或上同一个数,再根据上文的分析,那么整个序列将会被有操作的位置 \(p_1,p_2\cdots p_m\) 分割成 m 个互相独立的区间,其中每个区间内的数都异或上了同一个 \(x\),且满足 \(a_l\oplus x\le a_{l+r}\oplus x\le\cdots\le a_r\oplus x\)。于是这题就可以转为一个区间划分问题:将原序列划分为多段区间,每段区间应满足一定条件,且在区间的右端点处进行一次操作,求总操作的最小价值。
划分这东西是容易 dp,难点在于如何快速判断一段区间是否满足上述,异或上同一个数后不降的条件。要求一段序列具有单调性,只需保证任意相邻两项的单调性即可,于是我们考虑 \(a_i\oplus x\le a_{i+1}\oplus x\) 所需的 \(x\) 应满足什么条件:显然的充要条件,对于 \(a_i,a_{i+1}\) 的二进制表示,从高位开始第一个不同的位置是 \(k\) ,那么应该有 \(x_k=a_{i,k}\)。然后有了这个,我们在 dp 的时候固定右端点。移动左端点来 dp,就可以很方便的判断一段区间是否合法。
两个数异或同一个数,考虑二进制上第一个不同的高位。
一个集合的 \(\operatorname{mex}\) ,是其补集的最小值。 因此对于排列 \(q\) 的一段区间 \([l,r]\),其补集就是区间 \([1,l-1]\cup [r+1,n]\),取最小值后就是题目中的 \(\min(a_{l-1},b_{r+1})\)。因此发现,排列中任意区间的 \(\operatorname{mex}\) 都与排列本身无关,只与前后缀 \(\min\) 有关,于是贡献就分离了。算出所有区间 \(\operatorname{mex}\) 的和,最后乘上方案数即可。
如何计算任意区间 \(\operatorname{mex}\) 和。考虑用 \(\sum\limits_{i}^{\infin}[x\ge i]\) 来替换 \(x\) 这个技巧。原问题即 \(\sum\limits_{l\le r}\operatorname{mex}(l,r)=\sum\limits_{k}^{n}\sum\limits_{l\le r}[\operatorname{mex}(l,r)\ge k]\) 。
而计算 \(\sum\limits_{l\le r}[\operatorname{mex}(l,r)\ge k]\) 是容易的:只需要找到 \(q_i\in {1,2,\cdots,k}\) 这个集合的左端点和右端点,那么包含这个区间的所有区间都符合条件,贡献即为 \(l\times(n-r+1)\)。在这题中,枚举 \(k\) ,区间的左右端点是容易维护的。
方案数的计算也是简单的。
观察到题目给了很多不等式关系,且变量之间相互影响不好逐个确定,考虑使用差分约束。
\(l_{i,j}\le x_i+y_j\le r_{i,j}\Rightarrow l_{i,j}\le x_i-(-y_j)\le r_{i,j}\),这样就转换为了差分约束的标准形式了。再考虑题目中的额外限制,要保证 \((-y_j)\le 0,x_i\ge 0\),于是把这些不等式一起建图,就能解出 \(x_i,(-y_j)\) 的特解。
再考虑我们需要保证 \([x_1,\cdots,x_n,y_1,\cdots,y_n]\) 的字典序最小。可以发现,在差分约束中对一组变量跑最长路,得到的是 \(x_n-x_0\) 的最小值,同时,每个变量 \(x_i\) 都被卡到了其下界,任意变量擅自 \(-1\) 都会导致限制不再合法。发现这个东西就很符合字典序最小的限制啊,因为每个数都不能再变小了。
所以答案就是刚才建图跑最长路,跑出来的 \([x_1,\cdots,x_n,-(-y_1)_,\cdots,-(-y_n)]\) 吗?并非。
由于我们的答案是对 \((-y_i)\) 取反才能得到 \(y_i\),而为了保证 \(y_i\) 的字典序最小,实际上应该保证 \((-y_i)\) 的字典序最大才对,所以我们本应该对 \((-y_i)\) 跑最短路的!但是同一张图中,有可能既对 \(x_i\) 跑最长路,又对 \((-y_i)\) 跑最短路吗?显然不太可行。
但是我们发现,\(x_i\) 的优先级确实比 \(y_i\) 高,所以对图跑最长路得到的 \(x_i\) 是正确的,是字典序最小的解。既然 \(x_i\) 都已经求出来了,我们可以带入回题目的不等式中,求出 \(y_i\) 的范围,每个都取其下界即可保证 \(y_i\) 字典序最小。也就是说我们没必要一遍差分约束同时求出这两个东西,可以通过得出一部分,另一部分用模拟解决。
差分约束求最长路,得到的解在有下界约束的情况下,字典序最小。
AT_arc201_c [ARC201C] Prefix Covering
注意到与字符串前缀有关的条件,考虑 trie 树。
将问题转到 trie 树上考虑,就是 trie 树上有几个特殊点(字符串的结尾),选择一个特殊点可以覆盖其子树下的所有节点。每次加入一个新字符串,即增加一个特殊点,问有多少种选法,可以使整颗 trie 树下方(即所有叶子)都被覆盖。这东西显然考虑在 trie 树上作 dp 计数,容易设 \(f_i\) 表示覆盖以 i 这个节点为根的子树下方所有节点的选点方式。由于每次新增的一个点,只会影响到其父亲的答案,等于又跑了一遍 trie 树,所以回答所有询问的复杂度是 \(O(\sum |S|)\) 的。
AT_arc203_c [ARC203C] Destruction of Walls
注意到从 \((1,1)\) 走到 \((n,m)\) 至少需要删除 \(n+m-2\) 面墙壁,而题目中又限制了 \(k\le n+m\),因此显然是个分讨题目。
-
\(k<n+m-2\) ,答案为 \(0\)。
-
\(k=n+m-2\) ,两两路径删除的墙壁集合肯定不会相同,所以没有重复,答案为从 \((1,1)\) 到 \((n,m)\) 的路径数。即 \(\binom{n+m-2}{n-1}\)。
-
\(k=n+m-1\),可以在情况 2 的基础上再多删一条边。容易发现一个删边集合还是只会构成一条唯一合法路径,所以两两路径的集合还是不会相同。所以方案数为 \(\binom{n+m-2}{n-1}\times \left((n-2)m+(m-2)n+2\right)\)。
-
\(k=n+m-2\),答案是 \(\binom{n+m-2}{n-1}\times \binom{(n-2)m+(m-2)n+2}{2}\) 吗?并非。考虑一条路径,如果他有一个 “向下,向右” 的拐弯点,那么如果选择凹侧的那两面墙壁删除,就会在那里产生一条拐点为 “向右,向下” 的路径。这样,一个删边集合对应的路径不唯一,显然就会被算两次。考虑对这部分去重。容易发现,产生问题的这个拐弯点处,删除的墙壁构成了一个十字架,而从左上角走到右下角有两种方式,这就是问题的根源。我们只需要计数这样的十字架会出现多少次,减去即可。
不难列出十字架出现次数的一个和式:\(\sum\limits_{i=1}^{n-1}\sum\limits_{j=1}^{m-1}\binom{i+j-2}{i-1}\binom{n-i+m-j-2}{n-i-1}\),考虑优化它。
先将 \(j\to j-1\) ,那么原式等于 \(\sum\limits_{i=1}^{n-1}\sum\limits_{j=0}^{m-2}\binom{i+j-1}{i-1}\binom{n-i+m-j-3}{n-i-1}\),现在考虑快速计算内层循环 \(\sum\limits_{j=0}^{m-2}\binom{i+j-1}{i-1}\binom{n-i+m-j-3}{n-i-1}\)。观察这个式子,用其组合意义进行优化:这个和式,本质是一个枚举最大值的过程。考虑从 \(n+m-3\) 个东西中选出 \(n-1\) 个,并将前 \(i\) 个划分进某个集合 \(A\),而这个 \(j\) 就是在枚举被划入 \(A\) 集合的最后位置是哪里。容易发现,我们只需要选出了 \(n-1\) 个数,再将选出的前 \(i\) 个固定划入 \(A\) 集合即可,完全没必要用个 \(j\) 枚举最大的是哪个。因此在组合意义上我们就推出 \(\sum\limits_{j=0}^{m-2}\binom{i+j-1}{i-1}\binom{n-i+m-j-3}{n-i-1}=\binom{n+m-3}{n-1}\)。惊喜发现这东西与 \(i\) 无关,没必要再优化,原式直接变为 \((n-1)\times\binom{n+m-3}{n-1}\),这就是“十字架”的数量,也是我们多算了一次的部分,答案应减去。
但是还没完,由于删除墙壁的数量增多,我们甚至可以不选择走从 \((1,1)\) 到 \((n,m)\) 的最短路径。多于的两次删边允许我们反悔地,在行进过程中“向左”或者“向上”一次。那么我们就类似于对十字架那样的分析。发现这种操作的本质是在一个 \(2\times 3\) 或者 \(3\times 2\) 的矩形上的一次曲折移动。把这样有反悔操作的矩形拎出来计数,就会得到与上面类似的两个和式 \(\sum\limits_{i=2}^{n}\sum\limits_{j=1}^{m-2}\binom{i+j-2}{i-1}\binom{n-i+m-j-1}{n-i+1}\) 和 \(\sum\limits_{j=2}^{m}\sum\limits_{i=1}^{n-2}\binom{i+j-2}{j-1}\binom{n-i+m-j-1}{m-j+1}\),同样可以用组合计数的意义进行优化,得到 $(n-1)\binom{n+m-2}{n+1} $ 和 \((m-1)\binom{n+m-2}{m+1}\)。容易发现这样的反悔行进是独立于上面计算的额任何一种方案的,答案直接加上。
故最终答案的式子为 \(\binom{n+m-2}{n-1}\times \binom{(n-2)m+(m-2)n+2}{2}-\binom{n+m-3}{n-1}+(n-1)\binom{n+m-2}{n+1} +(m-1)\binom{n+m-2}{m+1}\)。
本题和式能进行组合意义优化,本质在于 \(j\) 的枚举范围非常合适。如 \(\sum\limits_{j=0}^{m-2}\binom{i+j-1}{i-1}\binom{n-i+m-j-3}{n-i-1}\),巧合的是,当 \(j=m-2\) 时,\(\binom{n-i+m-j-3}{n-i-1}=\binom{n-i-1}{n-i-1}\)。
AT_arc201_b [ARC201B] Binary Knapsack
考虑对每种重量都添加一个价值为 \(0\) 的物品,那么对于最终重量 \(< W\) 的最优解,都可以通过这些虚无物品凑成重量为 \(W\) 的情况,且价值不变。因此此题转换为恰好凑出 \(W\) 的情况下的最大价值,明显就可做许多了。
由于高位无法向下分解,我们从低位到高位枚举。考虑 \(W\) 二进制下的第 \(k\) 位,如果为 \(1\),由于选重量大于 \(2^k\) 的物品一定无法使最终重量的第 \(k\) 位为 \(1\),因此肯定要单独选出一个重量恰好为 \(2^k\) 的物品,显然我们贪心地选最大的的那个。此外,对于我们当前枚举到的 \(k\),除了已经用掉的那个,其他两两配对之后可以合并成重量为 \(2^{k+1}\) 的物品,因此将物品合并后上传即可进行下一步贪心。
当然,这题很难不联想到 P3188 [HNOI2007] 梦幻岛宝珠 的 dp,同样能做,但是复杂度是 \(O(n^2)\) 的。
猜测决策单调性,优化转移。
观察到复杂度瓶颈在于分组背包,最终得到的是 \(f_{j}=\max\limits_{k=1}^{cnt}(f'_{j+k}+v_k)\) 这么个形式的转移。且注意到 \(f_{j}\) 的决策点 \(p_j\) 具有单调性,即 \(p_j\) 随 \(j\) 增大非严格递增。可以考虑决策单调性优化 dp。
对于这种,被决策点 (\(f_j\)) 将来不会变成决策点 (\(f'_{j+k}\)) 的 dp,可以使用分治来进行决策单调性优化。已知 \([l,r]\) 范围内的被决策点,其决策点都属于 \([L,R]\) 范围内,那么我们可以暴力求出 \(mid=\frac{l+r}{2}\) 处的被决策点的决策点位置 \(pos\),然后根据决策单调性,递归解决 \(([l,mid-1],[L,pos]),([mid+1,r],[pos,R])\) 即可。由于每层中,被决策区间和决策区间都会被便利一次,一共 \(\log n\) 层,所以复杂度是 \(n\log n\) 的。
AT_arc189_b [ARC189B] Minimize Sum
画出数轴,观察一次操作的几何意义。假设 \(a_i=x_i-x_{i-1}\),发现,一次对称操作,就是交换了 \(a_i\) 和 \(a_{i+2}\) 。然后直接对着差分数组考虑贪心,发现答案可以用排序不等式取到,对着差分数组奇偶项分别排序即可。
AT_arc193_a [ARC193A] Complement Interval Graph
考虑从点 \(x\to y\) 至多要经过几个点。首先如果区间 \(x\) 和 \(y\) 不相交,那么显然不需要经过中间点;如果只经过一个中间点,显然中介 \(z\) 应保证与 \(x,y\) 的并集无交。若经过两个中间点,那么假设路径为 \(p_1=x,p_2,p_3,p_4=y\),那么容易画图分类讨论,发现该方案满足 \(x\) 与 \(p_1\) 不交,且 \(y\) 与 \(p_3\) 不交即可。继续画图观察,发现不可能有长度为 \(5\) 的路径存在,假设有,其子集一定也构成了一条路径,比长度为 \(5\) 更优。
根据上面的结论容易分讨得出答案。
坑点:只用三个点的路径不一定比用四个点的路径更优,因为用的可能不是同一批点,应取最小值。
T667229 R15 - 我想不出有趣的题目名称了所以这题就叫排列
分讨一定不能少。一定要考虑非平凡情况(比如这题 x 不递增有什么性质)
该题样例极具诈骗性质,只给出了 \(x_i\) 递增的情况。
考虑未在 \(x_i\) 中出现过的数 \(p\),将 \(p\) 插入到排列中,有多少种方式。显然的一个性质,如果 \(p\) 插入到 \(x_i\) 和 \(x_{i+1}\) 之间,那么就要保证 \(x_i<p,x_{i+1}<p\),如果插入到排列的开头就要保证 \(x_1<p\) ,插在末尾就要保证 \(x_m<p\),否则的话就可以通过调整选取的子序列,取到 \(p\) ,从而不符合题目条件。
继续观察插入这个过程:无论 \(p\) 插入哪里,都会在插入的地方增加多一个空位(\(p\) 插入后,\(p\) 前 和 \(p\) 后 都成为了可插入的空位)。且容易发现,对于 \(p'>p\),\(p'\) 能插入的位置一定包含 \(p\) 的能插的位置。有了这两条性质,从小到大枚举 \(p\),那么 \(p\) 能插入的位置个数是好维护的,乘法原理得到答案即可。
发现我们上面分析的做法压根就没要求 \(x\) 递增这个条件,所以我就以为 \(x\) 不递增的时候该做法不会出错。没想到还是犯了 充分条件 \(\ne\) 充要条件的错误:我的代码没用到这个性质,不代表 不具有这个性质不会对我的代码产生影响。还是分讨弱了。
考虑序列如果不递增,会产生什么影响。若 \(x_k<x_{k-1}\),考虑如果 \(x_k\) 后面选的数是“松”的(就是说后面还有选择的余地),那么我们显然可以通过多选一个 \(x_k\) 后面的数,而使得不选 \(x_{k-1}\) 用 \(x_k\) 顶替,这样字典序更小。因此,如果出现了第一个递减的位置 \(k\),那么其后面一定是“紧”的,我们不能插入任何一个数 \(p\) 进去。
所以我们实际上的做法,应该是找到第一个递减和的位置,就把后面的而空位卡掉,不纳入算法考虑当中。
题目要我们求,满足 前缀 和 后缀 两个限制的子序列的最长长度。显然的性质是,我们一定可以把所有的 \(1\) 都选上,只需要考虑每个 \(0\) 选不选即可。然后我们再考虑只满足 前缀 限制,和只满足 后缀 限制的两个子序列,显然答案要求的满足两个限制的子序列,一定是由这些只满足单独要求的子序列,删除一部分 \(0\) 得到的。于是我们找到了,满足单个限制的子序列和满足两个限制的子序列之间的关系,考虑利用 单限制 的答案求出双限制的答案。
容易发现 单限制 情况就类似括号序列,而维护括号序列的一些信息是可以上线段树的 ,所以我们考虑让 双限制 的答案也在线段树上维护。线段树要做的其实就是怎么合并两个区间。
先考虑解决 单限制 的情况:考虑得到区间 \([l,r]\) 内满足 前缀 限制的最长子序列,其左边一定是 \([l,mid]\) 内满足前缀限制的最长子序列。而 \([l,mid]\) 这部分子序列对右区间的影响,可以直接被概括为子序列中 \(1\) 的个数减去 \(0\) 的个数,这东西显然 \(\ge 0\)。考虑如果这东西 \(>0\),那么相当于我们合并后,右边原本满足前缀性质的子序列,的每一个前缀和都增加了这么个 \(1-0\),那么合并的时候我们就不能浪费这些馈赠,可以考虑往右边加一些没用过的 \(0\) ,在不超过左区间提供的 \(1-0\) 的情况下,使得合并后的子序列更长。合并 后缀 限制的最长子序列同理,考虑右区间对左区间的影响即可。
现在考虑维护 双限制 的答案。由上面的分析可知,我们要是想让双限制序列的长度变长,得添加 \(0\) 。而且这 \(0\) 还不能随便加:左区间内添加 \(0\),那么就必须是左边 前缀 子序列用过的 \(0\) ,否则左边就连前缀限制都满足不了;右区间添加 \(0\) ,就必须是右边 后缀 子序列用过的 \(0\),否则右边就连后缀限制都满足不了。所以,在一个区间内选出满足双限制的序列,他左边能选择的上限就是 左边的 前缀 子序列;右边能选择出来的上限就是 右边的 后缀子序列。
合并双限制序列,依然考虑右边的 \(1-0\),然后往左边添加 \(0\),这个添加的量还额外受到我们上面分析的上界影响。同理,添加完左边,我们还要尝试往右边添 \(0\),也是考虑左边 \(1-0\) 对右边的影响(注意,这里的左边是已经由上一步添加过了 \(0\) 的左边,所以一些数据在上一步的时候要更新一下)。然后合并就搞定了。
题解的做法更注意力一点。
考虑一个显然正确的贪心:先考虑让让序列满足前缀限制,那么就是从前往后,找到第一个不符合的位置,肯定是个 \(0\),把他删掉。然后前缀限制就满足了,然后再考虑后缀限制,再倒过来对后缀和做一次。直接维护这个贪心过程显然不太可能,考虑概括这个贪心最后会得到什么。
先考虑对前缀做的贪心。因为我们要子序列最长,那么就是删除的数最少,那就是最少操作次数,我们只关心上述贪心一共操作了多少次。考虑每一步贪心,我们都在前缀和第一个 \(<0\) 的位置,删除了一个 \(-1\),也就是说后面所有 \(<0\) 的位置都被 \(+1\) 了。而由于我们是在第一个非法位置操作的,所以操作其实等价于,我们对整个序列,每个前缀和 \(<0\) 的位置都 \(+1\) 了,那么操作的最小次数,显然就是前缀和的最小值的相反数。设前缀和为 \(a_i\),即 \(-\min\limits_{i=1}^n\{a_i\}\)。
设原本的后缀和为 \(b_i\),然后我们考虑经过了前缀操作后的后缀和 \(b_i'\),相对于 \(b_i\) 的变化了多少。显然要是我们第一轮贪心的时候删除了 \([i,n]\) 范围内的 \(0\) ,就会对 \(b_i'\) 产生影响。那么那么在这个范围内删除了多少个呢?考虑容斥,用总操作数减去我们在 \([1,i-1]\) 这范围内的操作数,而这个前缀操作数是可以直接套用我们上一段的分析得到,也就是 \(-\min\limits_{j=1}^{i-1}\{a_i\}\) 。因此,\(b_i'=b_i+(-\min\limits_{i=1}^n\{a_i\}-(-\min\limits_{j=1}^{i-1}\{a_i\}))=b_i-\min\limits_{i=1}^n\{a_i\}+\min\limits_{j=1}^{i-1}\{a_i\}\)
因此第二轮贪心的总操作数,也容易得到就是 \(-\min\limits_{i=1}^{n}\{b_i'\}\)。
那么总操作数就是 \(-\min\limits_{i=1}^{n}\{a_i\}-\min\limits_{i=1}^{n}\{b_i'\}=-\min\limits_{i=1}^{n}\{a_i\}-\min\limits_{i=1}^{n}\{b_i-\min\limits_{i=1}^n\{a_i\}+\min\limits_{j=1}^{i-1}\{a_i\}\}=-\min\limits_{i=1}^{n}\{a_i\}-\min\limits_{i=1}^{n}\{b_i+\min\limits_{j=1}^{i-1}\{a_i\}\}-\min\limits_{i=1}^n\{a_i\}=-\min\limits_{i=1}^{n}\{b_i+\min\limits_{j=1}^{i-1}\{a_i\}\}=-\min\limits_{1\le j<i\le n}^{n}\{b_i+a_j\}\)
转换到这里就非常可做了:观察 \(\min\limits_{1\le j<i\le n}^{n}\{b_i+a_j\}\) 这东西的形式,发现是一个前缀和+后缀和,那再考虑容斥,这玩意不就是整个序列,再扣掉一个区间后的和吗?所以要最小化这东西,就是要最大化中间扣掉的部分,就是一个最大子段和!线段树直接做就好了。
T667231 R15 - 凸多边形必须是凸的,此乃亘古不变之真理
我们规定凸多边形的一条边为 上边,意思是所有点都在这条边所在的直线上或者下方;同理我们定义 下边,表示所有点都在边所在的直线上或上方。
同时我们回顾利用叉姬计算凸多边形面积的过程,我们是按照某个顺序扫一遍多边形上的边,再将每条边的叉姬加起来再取绝对值,从而得到面积。而这么规定以后,凸多边形上的边,就会被分为 上边 和 下边 两部分,容易发现,如果 上边 的叉姬都是正的,下边 的叉姬都是负的,那么我们算出来的面积就是正确的。也就是说,我们通过给边一个分类,就可以去掉叉姬求多边形面积里面的那个讨厌的绝对值,每条边都独立,也不用关心扫的顺序,方便了我们对每条边的贡献进行计算。
所以现在我们可以直接针对某条边计算它的贡献。要分别计算这条边成为 上边 的贡献,和这条边成为 下边 的贡献。发现边对应的叉姬都是固定的,所以我们只需要统计这条边成为 上边 或 下边的次数即可,变成了一道计数题。
这个计数也挺简单的,也是一个排列计数的问题,我们找到某个单调性,然后判断当前考虑的数有多少种填法(注意减去之前的数占用的位置),乘法原理即可。枚举边是 \(O(n^4)\) ,计数可以双指针 \(O(n)\),于是总复杂度是 \(O(n^5)\)。
另外要特别注意一下去重:枚举到一条边,在这条线段的内部,可能别的点也会排列成一条边,刚好完全在现在这条边的内部。而我们计算内部那条边的贡献时,也会计算到他自己被包含的情况,而我们现在枚举到外面的这条边,又会被计算一次。不难发现,内部的边和外部的边的情况有重合,导致我们某些叉姬算了多次。因此考虑去重,我们强制要求我们现在枚举的这条边一定是“最外面的那层”边,也就是要求,横坐标在这条边两侧的点都不能位于这条边所在的直线上。这样子,相同形态的凸包,只会被最长的那条边计算一次叉姬,而不会被内部的小边多次计算。
线段包含的情况要考虑去重,对方案进行清晰的定位可以去重。

必须得先乘后除,否则会出现神秘re???

整除居然比 double 要慢????
前置
考虑超级钢琴思想的普遍情况。
寻找价值前 \(K\) 大方案具有固定套路:\(S_0\) 为价值最大的方案。\(\operatorname{trans}(S)\) 表示由方案 \(S\) 得到的后继方案集合,该函数应满足:
- \(v(S)\ge v(\operatorname{trans}(S))\)
- \(\operatorname{trans}(S)\) 集合大小应该适当(常数级,或 \(\log\) 级别)
- 所有合法方案,如果按照 \(S\to \operatorname{trans}(S)\) 连一条有向边,那么所有合法方案构成一颗以 \(S_0\) 为根的外向树。
如果设计的 \(\operatorname{trans}(S)\) 满足上述条件,那么前 \(K\) 大的集合一定是外向树上,包含根节点 \(S_0\) 的一个联通块。我们可以用堆来维护出这个前 \(K\) 大的联通块:初始时将 \(S_0\) 放入堆中;每次将堆顶 \(S\) 取出,再将 \(\operatorname{trans}(S)\) 集合中的方案放入堆中,以此重复 \(K\) 次。
如果 \(\operatorname{trans}(S)\) 满足条件,那么容易证明上述方法一定能不重不漏地,在 \(O(|\operatorname{trans}(S)|\cdot K)\) 的复杂度下找出前 \(K\) 大方案。
现在尝试解决,在一个序列 \(a\) 中,任意选出 \(m\) 个数相加作为价值,求出前 \(K\) 大选取方案的价值。
如果将 \(a\) 序列从大到小排序,那么选前 \(m\) 个显然是价值最大的方案,也就是 \(S_0\)。只需要设计出 \(\operatorname{trans}(S)\) ,那么这个问题就解决了。
我么先考虑如何用朴素的 dfs 解决这个问题: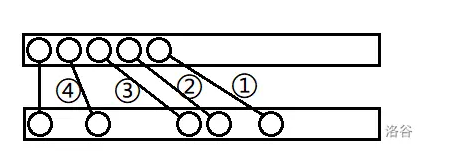
我们每次都向右移动若干位 最右端 未被标记过 的数,且不能越过任何已标记的数,然后将其打上标记。容易发现经过这样的移动,每一步的价值都比上一步要小,且这样的移动可以从 \(S_0\) 出发到达所有可能方案,所以我们可以根据这个暴力设计一个朴素的 \(\operatorname{trans}(S)\) 函数。
用一个四元组来描述一个方案,并用于转移:\((x,y,z,sum)\) 表示,前 \([1,x]\) 还未被考虑,当前要向右移动的位置是 \(y\) ,上一个已移动过的数位置在 \(z\),该方案的价值为 \(sum\)。那么 \((x,y,z,sum)\) 可以转移到 \((x-1,x,k,sum-a_y+a_k)\),表示 \(y\) 已经完成了移动,移动到了 \(k,k<z\) ,然后接下来考虑移动 \(x\),未被考虑的部分变为 \([1,x-1]\),并更新价值 \(sum\)。
由于我们还要枚举 \(k\),因此方案 \(S\) 的转移 \(\operatorname{trans}(S)\) 集合大小是 \(O(n)\) 级别的,考虑优化。
一个巧妙的 trick 就是,将枚举 \(k\) 一步转移,改成分步转移,每次都走一步。类似这个
本质上,是将外向树上,节点 \(u\) 的子节点 \(v\),都给串起来了。
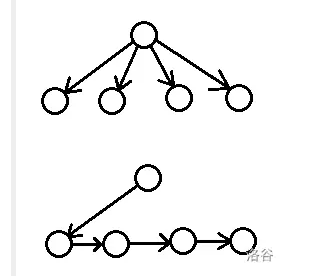
\((x,y,z,sum)\) 可以转移到 \((x,y+1,z,sum-a_y+a_{y+1})\) ,表示将 \(y\) 向右移动了一步,且不能超过 \(z\);或者转移到 \((x-1,x+1,y,sum-a_x+a_{x+1})\),表示 \(y\) 的移动已经完成,改为将 \(x\) 移动到 \(x+1\),未考虑的部分变为 \([1,x-1]\)。通过单步转移的方式,\(|\operatorname{trans}(S)|\) 是 \(O(1)\) 级别。至此,我们解决了这个问题。

上述算法已经帮我们解决了在固定选 \(k\) 个数的情况下,如何得到后继方案。这题中,我们需要解决选任意个数的后继方案,那么就维护 \(m\) 个上述算法,再将答案用超级钢琴的思路合并,即可得到任意个数的答案。
同理对于每个点的答案我们得到了,好需要合并成整颗数,那么依然是用超级钢琴的思路合并即可。
超级钢琴套超级钢琴。
注意到,我们每个点都要维护很多个队列来处理,但是容易分析出队列的总数是 \(O(n)\) 级别的,因此要开 vector<priority_queue<node>> q 这样的东西来防止炸空间。
实现出来挺厉害的。
点击查看代码
#include <bits/stdc++.h>
#define ll long long
using namespace std;
int n,k;
ll a[300010];
vector<int> g[300010];
struct node{
int x,y,z;
ll sum;
};
bool operator >(node aa,node bb){return aa.sum>bb.sum;}
bool operator <(node aa,node bb){return aa.sum<bb.sum;}
struct piano{
ll B;
bool emp=false;
vector<int> a;
vector<priority_queue<node>> q;
priority_queue<pair<ll,int>> Q;
void build(){
sort(a.begin(),a.end(),[](int aa,int bb){return aa>bb;});
priority_queue<node> tt;
for(int i=0;i<a.size();i++) q.push_back(tt);
priority_queue<node> ().swap(tt);
ll tmp=0;
if(a.size()<3){emp=false;return ;}
for(int i=0;i<2;i++) tmp+=a[i];
for(int i=2;i<a.size();i++){
tmp+=a[i];
q[i].push((node){i-1,i,(ll)(1e9),tmp});
Q.push({tmp,i});
}
}
ll top(){ return Q.top().first+B; }
void nxt(){
int id=Q.top().second;
Q.pop();
node u=q[id].top();
q[id].pop();
if(u.y+1<u.z&&u.y+1<a.size()) q[id].push((node){u.x,u.y+1,u.z,u.sum-a[u.y]+a[u.y+1]});
if(u.x>=0&&u.x+1<a.size()&&u.x+1<u.y) q[id].push((node){u.x-1,u.x+1,u.y,u.sum-a[u.x]+a[u.x+1]});
if(!q[id].empty()) Q.push({q[id].top().sum,id});
if(Q.empty()) emp=false;
}
} d[300010];
priority_queue<pair<ll,int>> q;
int main(){
// freopen("b.in","r",stdin);
// freopen("b.out","w",stdout);
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
cin>>n>>k;
for(int i=1;i<=n;i++) cin>>a[i];
for(int i=1;i<n;i++){
int aa,bb;
cin>>aa>>bb;
g[aa].push_back(bb);
g[bb].push_back(aa);
}
for(int i=1;i<=n;i++) sort(g[i].begin(),g[i].end(),[](int aa,int bb){ return a[aa]>a[bb]; });
for(int i=1;i<=n;i++){
d[i].B=a[i];
for(int j=0;j<g[i].size();j++){
d[i].a.push_back(a[g[i][j]]),d[i].emp=true;
}
}
for(int i=1;i<=n;i++) if(d[i].emp) d[i].build();
for(int i=1;i<=n;i++) if(d[i].emp) q.push({d[i].top(),i});
ll ans=0ll;
for(int i=1;i<=k;i++){
ans^=abs(q.top().first);
int id=q.top().second;
q.pop();
d[id].nxt();
if(d[id].emp) q.push({d[id].top(),id});
}
cout<<ans;
return 0;
}
AT_arc194_d [ARC194D] Reverse Brackets
一开始容易想到区间 dp ,但是发现翻转操作是可以重叠的,也就是说左边区间的东西可能去到右边去,然后再在右边区间里交换。这样子两个不同的区间不具有划分性,合并的时候并不彼此独立,也就无法使用区间 dp 了。
转为考虑翻转操作的性质。现有 (A) 形式的字符串,其中 A 是一个合法括号串或空串,我们称 (A) 为一个 整括号串。那么原括号串就是由多个整括号串链接而成,即 (A)(B)...(Z)。考虑翻转操作可以只对相邻的两个整括号串进行,那么一次就相当于一次邻项交换。而我们可以进行任意次操作,也就是说我们可以将原括号串,以整括号串为单位,进行任意重排。
经过这样的思考,每个整括号串内部就是一个独立的子问题了,我们实现了问题的划分,可以递归下去处理。此时括号间的关系就构成了一棵树形结构。
但是还要考虑去重的问题,因为有可能两个原本不同的整括号串,经过内部的重排后可以变成相同的。我们发现,如果存在这样一对经过重排可以变成相等的整括号串,那么他们两一定是完全等价的( a 能形成的括号串,b 也能形成)。而对于原串来说,交换这些本质相同的整括号串间的顺序是没有意义的,也就是说这其实是一个 有重复元素重排 的问题。答案就是 \(\frac{n!}{cnt_1!\cdot cnt_2!\cdots cnt_m!}\),其中 \(cnt_i\) 是元素 \(i\) 出现的次数,因为同种元素之间交换顺序没有意义。所以我们只需要解决,每种整括号串的个数即可,也就是需要快速判断整括号串是否相等。注意到上面我们已经发现了由这种递归方法,括号串形成了一棵树,不难发现整括号串就是一颗子树,如果两颗子树同构,那么两个整括号串就是相等的。因此可以用树哈希判断。
树哈希 : \(h(u)=(1+\sum\limits_{v}g(h(v)))\mod p\),其中 \(g(x)\) 是一个变换函数,一般考虑 xor hash。
一堆复杂的东西判断相等,考虑哈希。
AT_arc189_d [ARC189D] Takahashi is Slime
如果每次合并的条件都是,新元素比当前元素大,那么至多合并 \(\log V\) 次,因为每次合并当前元素大小都会翻倍。
对于每个位置,每次二分出一段区间,这段区间内所有元素都比该数当前大小要小,然后该数就可以吃掉这一段数,更新当前大小。可以进行多步这个拓展的过程,因为如果吃掉了一段,后面又能再吃,那么大小至少翻一倍,因此拓展至多只会进行 \(O(\log V)\) 次,复杂度是对的。
sol2:容易发现,如果将每个数能吃掉的位置看成一个区间,那么两两区间只会有包含或不交关系(不会有简单的相交情况,因为通过分析发现,相交的两个区间一定能拓展为包含)。利用这个性质,我们可以设计出算法达到非常优的复杂度。未完待续……
首先容易写出暴力 dp 做法:设 \(f_{i,j}\) 表示已经处理完前 \(i\) 段草坪,最后割草机内存着体积为 \(j,j\le C\) 的草时的最短时间。转移就是从第 \(i-1\) 段草坪转移到第 \(i\) 段草坪,我们枚举一个 \(k\) 表示在处理第 \(i\) 段时要进行 \(k\) 次清空,那么就能算出第 \(i-1\) 段末尾时我们放了多少。也就是 $f_{i,j}=\min(f_{i-1,\min(j-v_i+k\cdot C,C)}+k\cdot (a_i+b)+a_i),j-v_i+k\cdot C\in [0,2C) $,同时我们在草坪的末尾还可以进行一次清空,因此 \(f_{i,0}=\min(f_{i,j}+b),j\in [0,C]\)。
考虑优化上述转移,发现当 \(k\) 满足 \(j-v_i+k\cdot C\in [0,2C)\) 时,\(k\) 其实只有 \(\max(0,\left\lceil \frac{v_i-j}{C}\right\rceil)\) 这一种取值是合法的,所以没必要枚举 \(k\)。转移变为 $f_{i,j}=\min(f_{i-1,j-v_i+\max(0,\left\lceil \frac{v_i-j}{C}\right\rceil)\cdot C}+\max(0,\left\lceil \frac{v_i-j}{C}\right\rceil)\cdot (a_i+b)+a_i) $。
此时需要注意到 \(j-v_i+\max(0,\left\lceil \frac{v_i-j}{C}\right\rceil)\cdot C\) 这玩意,它等价于 \(x\ge 0,x\equiv j-v_i\pmod C\)!这个关键的性质提示我们要把状态 \(j\),放到\(\mod C\) 的同余系内考虑。但是 \(C\) 的同余系只有 \([0,C-1]\),而我们上述转移中 \(j\in[0,C]\),考虑如何处理 \(j=C\) 的影响。我们发现,如果将状态 \(j\) 都放入同余系,那么由于 \(C\equiv 0\pmod C\),因此 \(f_{i,C} 和 f_{i,0}\) 实际上是对应的同一个状态,而根据对这个 $f_{i,j}=\min(f_{i-1,j-v_i+\max(0,\left\lceil \frac{v_i-j}{C}\right\rceil)\cdot C}+\max(0,\left\lceil \frac{v_i-j}{C}\right\rceil)\cdot (a_i+b)+a_i) $ 转移方程观察,如果我们要求最终状态必须为空(即使用一次清空),那么此时一定有 \(f_{i,C}+b\le f_{i,0}\),因此保留 \(f_{i,C}\) 一定比保留 \(f_{i, 0}\) 更优秀。于是,我们可以用 \(f_{i,C}+b\) 来顶替掉原本的 \(f_{i,0}\),用 \(f_{i,C}+b\) 的值来作为 \(f_{i,0}\) 的值,两者共用一个状态。 因为他们效果是一样的,且前者更优。对应到原方程,就是我们转移的时候,仅考虑 \(j\in[1,C]\) 的状态,并令单独令 \(f_{i,0}=f_{i,C}+b\),在同余系中,由于 \(C\) 与 \(0\) 作为同一个状态,直接转移就没有问题了。
现将原 dp 方程的 \(j\) 状态都放在 \(C\) 的同于系内考虑,那么转移就相当于,先将整个序列进行一次向右 \(v_i\) 个单位的 循环平移。
继续考虑转移中,后面的加法部分如何优化。发现,由于 \(k=\left\lceil \frac{v_i-j}{C}\right\rceil\),而 \(j\in[1,C]\) ,因此对于相同的 \(i\) ,其实只有 \(k\) 和 \(k-1\) 有可能产生贡献!因此,对于 \(i\) 相同的所有状态,有一部分会由 \(k\) 贡献,有一部分会由 \(k-1\) 贡献,显然这部分是 \(O(1)\) 个区间加法!
综上,我们只需要全局平移,再通过分讨 \(j\) 的大小关系得到加法更新的区间,然后执行若干个区间上的区间加法,这样就完成了一次对 dp 数组的更新。我们发现这东西很有机会用线段树进行维护。
考虑平移是对全局起作用的,而且是循环平移,因此我们没必要真的维护平移这个操作,而是记录平移的偏移量。考虑不是对全局进行平移,而是对修改的区间进行平移,这是非常容易的。同时,由于修改是 \(O(n)\) 的,因此我们直接对修改的端点进行离散化,就能通过维护一颗支持区间加以及全局最小值的线段树解决这个问题。
首先要理解,当 \(m=0\) 时,当且仅当 \(n\equiv 0\pmod{K+1}\) 时 \(f(n,k)=-1\)。显然直接从最终状态开始倒推即可理解。
这个问题貌似只能通过枚举 \(k\) 来解决,因为 \(k\) 不同的时候局面之间没有什么有用的共性。
先考虑仅处理 \(m=0\) 的情况,如何解决 \(N\le 10^6\) 的部分。答案是要求 \(\sum\limits_{n,k}f(n,k)\times (n\oplus k)\),这个异或感觉没啥好性质可以跟博弈函数联系。但是我们发现,如果不管博弈函数,\(\sum\limits_{n,k}(n\oplus k)\) 是好求的:我们计算每一位二进制位的贡献即可,容易在 $n\log n $ 的复杂度内计算。然后再注意到,对于一个 \(k\) ,先手必败态的 \(n\) 一定是 \(k+1\) 的倍数。而存在倍数关系,那么可以想到调和级数,也就是说,\(f(n,k)=-1\) 的数对数量是 \(n\ln n\) 级别的。于是我们直接容斥,用 \(\sum\limits_{n,k}(n\oplus k)\) 暴力减去这部分必败态的贡献即可。
然后是增加了 \(m\) 个位置 \(a_i\),当先手位于这个位置的时候一定是必胜的,这是题目的条件。简单分析可以发现,在我们枚举出了一个 \(k\) 的情况下,\([1,N]\) 内的位置,胜负状态已经确定了。我们从小到大考虑 \(a_i\),如果 \(a_i\) 位置本身就是必胜的,那么 \(a_i\) 其实没有影响;反之,如果 \(a_i\) 位置原本是必败的,由于一到达 \(a_i\) 就赢了,因此此时 \(a_i\) 就变成了必胜态,而 \(a_i+1\) 就变成了必败态(因为他能到的所有猴急状态都是必胜的)。我们从 \(1\) 到 \(N\) 模拟这个更新的过程,即可得到问题的答案。由于还要枚举 \(K\) 所以复杂度是 \(O(N^2)\) 的。
再来考虑正解做法。\(m=0\) 时的情况提示我们,必败态一定不会太多,因此我们继续考虑暴力计算必败态的贡献,然后减去即可。容易发现,这个结论是对的,哪怕增加了 \(m\) 个必胜点,必败态数对 \((n,k)\) 的数量仍是 \(N\ln N\) 级别的。因为我们发现,从小到大每加入一个必胜点 \(a_i\) ,对原本必败态的影响就只是,往后挪动了一个位置而已,没有引起更大的变化。 而必败态之间是固定相隔 \(K+1\) 的,若跳到了一个必胜点 \(a_i\),那么继续往后跳即可。因此容易实现一个算法,使得我们每一步跳到的位置,都是必败态,那么复杂度就是 \(O(N\ln N)\) 了。
由于数据范围比较小,我们可以直接考虑一些比较暴力的思路。我们直接考虑搜索剑爵给哪些蛋糕,分配多少的权值。直接搜肯定不行,贪心优化一下:肯定要用完 \(m_2\) ,答案不会更劣;肯定蛋糕的 \(a_i\) 越大,所分配的权值也就应该相对越大,也就是说如果按照 \(a_i\) 降序排序的话,所分配的权值应该单调不升。然后这个东西,我们发现就是一个划分数的问题,有一个很典的 \(dp\) 来计算方案数:设 \(f_{i,j}\) 表示将 \(i\) 分成 \(k\) 份,分成的数单调不降的方案数。转移就是 \(f_{i,j}=f_{i-1,j-1}+f_{i-j,j}\),就是考虑新增一个 \(1\),或者已分好的所有数都减去 \(1\)。通过这个 \(dp\) 我们就发现,当 \(m_2\le 30\) 时,\(\sum\limits_{j=0}^nf_{30,j}\) 实际上只有 \(6000\) 左右,完全支持暴搜找方案。
于是我们就把剑爵所有可能得分配方案都找出来了,那么我们的凯瑟只需要见招拆招,对与每种分配方式都找到一个最大的方案拿走蛋糕即可。显然剑爵没给权值的蛋糕都直接归凯撒,这些蛋糕可以不用管。然后就是凯撒要抢走剑爵已经赋了权值为 \(w_i\) 的蛋糕 \(a_i\),那么凯撒就至少也只需要给这个蛋糕分配 \(w_i\) 的权值即可。总权值不能超过 \(m_1\) 。这显然是一个 01 背包问题,直接做就好了。所以我们就知道了,对于每种剑爵的分配方式,凯撒最优能拿到多少蛋糕。
由于剑爵绝顶聪明且有主动权,因此答案是凯撒能拿到的最优数量蛋糕,的最小值。
我是从菊花图的部分分开始分析,然后得到正解思路的。
题解介绍了一个很有意思词:守恒量。我们考虑这道题是什么守恒:当操作的路径长度为偶数时,无论选择什么 \(x\) 进行操作,整张图的 \(\sum\limits_{i} a_i\) 都不会变,因为一加一减抵消了。而如果选择的路径是奇数,那么 \(\sum\limits_{i} a_i\) 将会增加 \(x\)。
考虑菊花图的时候,我们只能操作长度为 \(2\) 的路径。数据保证一定有解,所以一定有 \(\sum\limits_{i} a_i=\sum\limits_{i} b_i\)。那么我们尝试贪心的操作:随便找出一条边称为 根边,然后枚举所有非根边,如果当前边比目标值大了,就将这条边减小 \(x\) 使其满足条件,同时根边增加 \(x\);否则则相反操作。我们发现,这样子一轮下来,最终所有非根边都满足了条件,只剩根边。而由于 \(\sum\limits_{i} a_i=\sum\limits_{i} b_i\) 始终成立,这说明我们的根边在进行了这么多次操作后,最后一定等于他的目标值,因此整张图就解决了,这是菊花图部分的做法。
我们考虑将菊花图的想法拓展到树上:考虑选择一个度数为 \(1\) 的点作为整棵树的根,它向下延伸的那条边作为 根边。然后我们从根边下方的那个节点开始,自底向上地,从叶子上方的边开始贪心地调整使得其满足条件,每次都操作一条长度为 \(2\) 的路径,其由当前被调整的边和他的父亲边构成。容易发现,这么一轮下来,所有非根边都将满足条件,而当 \(\sum\limits_{i} a_i=\sum\limits_{i} b_i\) 时,根边也将满足条件。问题是 \(\sum\limits_{i} a_i\ne\sum\limits_{i} b_i\) 时,这时我们就可以考虑将情况规约:既然不相等的时候不行,那我通过操作把你变成相等不就行了?这时就需要我们操作奇数条边了,因为他可以改变 \(a\) 的和。我们只需要随便操作一条长度为 \(3\) 的路径,使得最终满足 \(\sum\limits_{i} a_i=\sum\limits_{i} b_i\) ,然后再进行一遍贪心即可。
限制相当抽象,直接做一般都做不出来。考虑通过严格的限制,得到一些突破的性质。
观察第二三条限制,发现这等价于与黑点坐标有关的一些值构成了一个 排列。那么说明黑点的数量必须恰好为 \(n\) ,也就是 \(\sum a_i=n\),否则无解。发现 一 限制没啥约束力度,而 二 三 限制对网格形成了相当的严格限制,且他们单独作用的时候,网格并不具有什么良好的性质,因此我们猜测当 二 三 性质同时启作用的时候网格将会出现良好性质。注意到,同一列中必然只能放一个黑点,否则肯定至少会违反 二 三 限制的其中一个;结合前面这个性质,继续手玩,发现为了同时满足 二 三 性质,我们可以也尽可以在网格上方一个倒三角的区域放置黑点,且要求每列只能放一个,可以随意防止且不会违反二三限制。因此,二三限制被我们转为了一个很具体的条件,然后再来考虑满足一限制,直接用排列计数常用套路,乘法原理即可。
AT_arc189_c [ARC189C] Balls and Boxes
考虑将篮球与红球分开来讨论。对于每种颜色,一个点会有恰好一个出度,也会有恰好一个入度(因为保证是排列),因此得到的图一定是若干个个环。那么就容易判断无解的情况。对于红色来说,考虑点 \(u\) 为最终有球的位置,那么只需要找到距离 \(u\) 最远的,有该种颜色球的位置 \(v\) ,那么显然依次移动 \(dis(v,u)\) 路径上的点,就能使得所有该种颜色的球在 \(u\) 点。再考虑蓝色也是同理。显然我们找到了一个合法操作,那就是先处理红色的情况,再处理蓝色的情况。但是这样操作数是 \(dis(v_0,u)+dis(v_1,u)\) 的,不一定最小。发现优化操作数的点在于,我们可以在某些点,同时完成蓝色和红色球的移动。思考一下就会发现,这些公共点,构成了 蓝色操作序列 和 红色操作序列 的一个公共子序列。因此,为了使总操作数最少,那么就是使尽可能多的操作“一石二鸟”,也就是找出两个操作序列的最长公共子序列即可。
考虑查询的 \(K\) 固定的版本:
线段树上维护单调栈信息,考虑线段树二分。
容易想到考虑每个数会对多少个区间产生贡献,同时由于有相同的数,还要考虑去重问题:对于每个位置 \(i\),我们维护 \(L_i\) 表示第 \(i\) 个数左边第一个比它大的位置,\(R_i\) 表示右边第一个大于等于它的位置,那么位置 \(i\) 将会对 \({L_i+1,R_i-1}\) 内包含 \(i\) 且长度为 \(k\) 的所有滑动区间产生 \(a_i\) 的贡献。
一开始有一个错误的思路:我们考虑维护每个位置的这么个 \(L_i,R_i\),使其支持单点修改。但这个问题是麻烦的,难点在于一次单点修改,不仅会影响该次修改的这个点的 \(L_i,R_i\) ,还会影响在他附近的一系列点的信息。而对于不构成完整区间的一系列点的修改,我们是没法做的。
思考上面算法的问题在哪。按 \(a_i\) 单独考虑贡献这个大方向是没错的,问题就出 我们想要动态维护出每一个点的信息,然后正面去统计答案。 这其实是不优的。
考虑我们应该如何计算答案:除了正面计算,其实我们还可以选择关注每次修改操作后,答案的 增量 。这是个经典的思想。我们很难维护一段区间内的点的贡献,而且也不方便修改,但是查询每个单点,它的 \(L_i,R_i\) 是多少是方便的,只需要维护序列上的一些简单信息,再线段树二分即可。也就是说我们可以准确的知道当前修改的这个位置它的 \(L,R\) 信息,那么这次修改对整体答案的影响就是 \(\operatorname{con(L',R')}-\operatorname{con(L,R)}\),其中 \(\operatorname{con(L,R)}\) 表示在范围 \([L,R]\) 内滑动长度为 \(k\) 的区间的贡献,\(L',R'\) 是修改后,该点新的信息。
我们的线段树本质上是在维护,查询增量所需的信息。
上面的一大轮分析都是在读错题的前提下完成的()。实际上,每次查询的 \(k\) 是会变的,因此我们无法使用上述算法解决问题,因为上述算法依赖于 一开始处理出初始答案,再维护增量。
那我们的原先的思考就完全没有意义吗?其实也不是。
容易想到转换:\(A_i=a_i-i,B_i=b_i-i\)
我们只关心最终联通块的数量,并不关心每个联通块内的成员,因此可以开始考虑一些不基于并查集优化连边的算法。
套路地向将元素按照 \(A\) 升序排列,去掉一维限制。现在连边的条件变成对于 \(j\) 找到 \(i<j,B_i>B_j\) 来连边。直接考虑优化连边没有什么想法,可以考虑将点与点间连边的过程看成是点与集合的合并。显然只要集合 \(X\) 外部的一个点 \(u\) 与集合中的某个元素连了边,那么点 \(u\) 就并入了集合 \(X\) 当中。由于我们只关心点 \(u\) 和集合中的某个点,这提升我们要为集合 \(X\) 找一个代表元素 \(v\),使得只需要判断点 \(u\) 是否能和 \(v\) 连边,就能直接判断点 \(u\) 是否能并入集合 \(X\) 中。显然应该选取集合中 \(B\) 值最大的点作为 \(v\)。算法雏形已经出现,我们只需要对于每个点 \(u\) 尝试并入现有的集合中,或者新开一个集合即可。由于考虑每个点的顺序显然不影响最终答案,于是我们正序扫一遍整个序列即可,判断能并入哪些集合只需要维护一个类似单调栈的结构表示现存所有集合的代表元素即可。
upd: 维护连通块信息,连边 就相当于合并两个集合。于是考虑借用并查集的思想,为集合找一个 代表元素,使得仅用少量信息即可描述集合形状,方便合并判断。
将零散的操作整合成一个单位元操作 : C+ 表示将最后一个数乘 \(2\),1+ 表示将最后一个数 \(+1\)。显然通过这两个操作就可以在二进制的基础上在序列的最后一位以 \(O(log V)\) 的操作数构造出任何数。由于每次调用 + 都会对之前的数产生影响,这提示我们要倒序构造,以方便处理在考虑当前这位的时候,要弥补多少后面会带来的影响。
首先要从题目中找到一些基本的性质,然后才能联想到 \(dp\) 状态的设立,再对转移进行推式子优化。
由于值域达到了 \(2^n\) 级别,我们先计数的时候显然不能再考虑某个具体的数字,比如 \(114514\) 之类的——我们只能聚焦与每个二进制位之间的差别与联系。但光是这点思考还不足以令我们想出 dp 状态和转移,继续分析。考虑只针对一个二进制位对序列进行观察,比如说最高位为第 \(n\) 位的情况:由于序列严格递增,那么一定构成形如 0 0 0 ... 0 0 1 1 1 ... 1 这样的结构。根据异或的性质,要保证 \(i\oplus j=k\) ,那么 \(i,j,k\) 肯定不可能同时在第 \(n\) 位处为 \(1\),要么第 \(n\) 位均为 \(0\),要么构成 0 1 1 这样的结构。注意到如果保证第 \(n\) 位均为 \(0\) ,那么就等于我们将最高位消掉了,将整个序列的值域从 \(2^n\to 2^{n-1}\),变成了一个子问题!这正是我们先想要的,因为这有助于我们设立状态。考虑设 \(f_n\) 表示在值域为 \([1,2^n]\) 内选数,且最后一个数的第 \(n\) 位为 \(1\) 的序列个数。那么最终答案就是 \(\sum\limits_{i=1}^{n}f_i\)。通过大力推式子可以写出转移:
容易优化成 \(O(n)\)。
考虑从整个操作过程中,抽象出一些关键的量来作为 dp 的状态。dp 是对问题的一种抽象刻画。
考虑整个取球的过程中,我们不考虑球的编号,那么每次取出球实际上有三种状态:取出了之前没取过的球,取出了之前只取了一次的球,取出了之前取了多次的球。我们发现,由于我们并不关心总取球次数,那么 取出之前取过多次的球 这个状态实际上没有任何意义,他既不会影响我们 取恰好一次 的集合,也不会影响我们的 已取集合。因此这其实是一个无效状态,有和没有都一样,少取这一次和多取这一次都一样,因此我们接下来可以钦定整个过程中,取球只会有 取到新球 和 取到之前恰好取一次的球 两种状态,也就是说把无用状态直接完全忽略。通过以上的分析,我们绕开了一个处理起来很麻烦的无用状态,dp 转移将变得清晰。
显然整个过程中的关键量,是 已被取过的球的集合 和 恰好被取一次的球的集合。但注意到,不同编号的球是完全等价的,所以实际上我们只需要钦定 \([1,i]\) 范围内的球是被取过的,\([1,j]\) 范围内的球是被恰好取过一次的,也就是说我们没必要记录整个集合的具体信息,我们只需要记录集合的大小就足以描述一个状态。那么很容易想到应该设 \(f_{i,j}\) 表示达到上述状态的概率。有 \(j\) 个球恰好被取过一次,\(n-i\) 个球还没被取,那么每次取球就是从这 \(n-i+j\) 范围内挑一个(因为我们已经忽略了一部分无用状态),那么就有转移:
有了每个状态的概率,我们求期望只需要用期望的定义,求状态的加权平均数即可。
看到字典序最小,就是要让越前面的数越小越好。所以一个很一眼的思路就是,将序列抽象成一颗完全二叉树,然后就是层次遍历每个节点,可以考虑和其两个子节点交换——显然要保证子树的根节点都要比其子节点要小。到这一步为止都很简单,但我却以为这样子就做完了,因为我没有意识到 与子节点交换 这个操作是有任意度,比如说样例:
原本的树结构如左图所示,如果 c 是整个结构的最小值,那么交换后一共有两种可能:
a c c
/ \ -> / \ or / \
b c a b b a
说明我们原本的贪心策略还不够唯一确定最小字典序的序列。于是我参考样例,得出了一个错误的策略:当 a 小时放左边,当 a 大时放右边。显然如果 a b 一直位于同一层这个贪心显然是对的,但是由于两颗子树内部还会对根节点进行轮换,也就是说 a b 最终很可能不是在同一层,这样子就不太好比较最终那种情况的字典序比较小。
此时贪心貌似陷入瓶颈了,但是因该注意到这个做法是有前途的,继续深入思考可以发现正确的贪心思路。
不妨假设 \(a\le b\),左子树编号为 \(2k\) ,右子树编号为 \(2k+1\),设 \(f(x,a)\) 表示把 \(a\) 作为编号为 \(x\) 的子树的根时,\(a\) 在所有操作后 最终位置 的最小可能编号是多少。那么贪心思路就是,\(f(2k,a)\) 和 \(f(2k+1,a)\) 哪边小放哪边。
证明这个策略则是考虑,在最终序列 \([1,\min(f(2k,a),f(2k+1,a)))\) 这段区间内的数,一定不会受 \(a\) 是放左子树还是右子树的影响(因为当 \(a\) 放得考前的时候他们有办法超上来,那么当 \(a\) 放得靠后的时候,他们显然一样能超上来,且 \(a\) 原本位置的数 的变劣不会给任何 原本不在这段区间内的数 超车的机会,也就是说不会有新的数进入到这段区间)。
至于怎么求出这个 \(f(x,a)\),直接暴搜模拟的话复杂度是 \(O(n^2)\) 的,由于状态数本身就是 \(O(n^2)\) 的,因此加了记忆化也不会有改变。但是注意到,对于子树 \(x\),其大小为 \(S_x\),那么对于所有 \(a\) 进行离散化后,能让 \(f(x,a)\) 产生差异,本质不同的 \(a\) 其实只有 \(S_x+1\) 个。有了这个性质,那么总状态数就是 \(O(\sum\limits_{i}^{n}S_i)=O(n\log n)\),这个式子就是完全二叉树的所有子树大小的和,证明考虑每个节点只会被其祖先统计到,而树高是 \(O(\log n)\) 的。
实现的话可以用 unordered_map 来存储 \(f(x,a)\),一共只会存 \(O(n\log n)\) 个元素所以不会爆空间。
先对所有有用的时间点离散化,然后我们顺着扫一遍时间轴,维护一个数组 \(f_i\) ,表示在到当前时刻位置,且当前时刻为空余时(没有在进行任务),呆在 \(i\) 号节点所能完成的最大任务数量。转移就直接模拟即可,由于我们保证了目前处于空余时的最大收益,因此这么维护这个过程最终答案 \(\max\limits_{i=1}^{n} f_i\) 显然是对的。
CF1552E Colors and Intervals 此题中,我们有了一个关于 单点被覆盖次数 的限制,那么就可以考虑把 单点被覆盖次数 这个东西转换为 多个序列内互不相交的区间序列 的序列个数。
多个区间进行覆盖,考虑与 某个点 被覆盖的次数进行联系。
T645364 R7C - AVE 此题中,有多个区间序列,每个序列内的区间互不相交。考虑将区间序列的个数与单点上被覆盖次数联系求解。而在CF1552E Colors and Intervals 此题中,我们有了一个关于 单点被覆盖次数 的限制,那么就可以考虑把 单点被覆盖次数 这个东西转换为 多个 由互不相交的区间组成的区间序列 的序列个数。
题目中要求每个点被覆盖的次数至多是 $\left \lceil \frac{n}{k-1} \right \rceil $,这玩意的形式很特殊,要进行联想。我们一共要选出 \(n\) 个区间,我们利用单点覆盖数这一限制,将其展开为对区间划分的限制:选出多个区间序列,除去一个序列,其余单个序列所含的区间 的个数 必须恰好为 \(k-1\);并且所有序列内的区间必须互不相交。显然这样子我们就会选出 $\left \lceil \frac{n}{k-1} \right \rceil $ 个区间序列,并且这些序列的区间即使叠加在一起,单点的覆盖次数也不会超过 $\left \lceil \frac{n}{k-1} \right \rceil $。
因此问题就经过了一步小转化,变成了要求我们一共进行 $\left \lceil \frac{n}{k-1} \right \rceil $ 轮操作,每轮操作中都在原序列中挑出 \(k-1\) 个颜色还没被用过的区间,且这 \(k-1\) 个区间互不相交。直到所有颜色都被用过为止。
考虑我们如何尽可能优的,从原序列中挑出 \(k-1\) 个不相交区间,且这个过程还能持续 $\left \lceil \frac{n}{k-1} \right \rceil $ 轮。我们考虑在本轮中,已经选出来的区间最远的右端点位置为 \(R\),我们要在剩下可选区间中,在满足 \(l_i>R\) 的区间集合内,选 \(r_i\) 最小的那个区间作为下一个选择的区间,并将该颜色标为已用,并更新 \(R\)。持续这个过程直到选出了 \(k-1\) 个区间。
由于每种颜色被用过后就不会再用了,于是可以等效为把该种颜色从原序列中全部删除。可以发现这是不影响后面的区间选取的。因此,前面进行区间选取,不会影响到当前轮,也就是说轮与轮的贪心是独立的。我们只需要证明,我们使用上述贪心策略,一定能取出 \(k-1\) 个区间即可。考虑使用 归纳法。
由于我们只需要选出 \(k-1\) 个区间,因此序列中只有 \(k-1\) 种颜色是有效的,我们可以任意选择 \(k-1\) 种颜色保留,剩下别的颜色的数直接删除。那么原问题就可以描述为有 \(k-1\) 种颜色,每个颜色有 \(k\) 个数,能否选 \(k-1\) 个区间的问题。我们定义该问题为 \(Q(k-1,k)\)。考虑上述贪心过程中,我们选出了第一个区间,设他的右端点为 \(r\) ,那么在 \([1,r)\) 范围内,每个元素的颜色肯定都互不相同,否则我们就可以选择前面的区间而不是这个 \(r\)。因为我们选出了这么一个区间,那么这种颜色在往后的贪心过程中就不能用了,可以把后面的这种颜色的元素都删掉,此时颜色总数变为了 \(k-2\)。而对于在 \([1,r)\) 中出现过的颜色,均已经被用掉了一次,也就是说这些颜色的元素个数在后面的贪心过程中等价为 \(k-1\)。此时可以发现,在下一步贪心中,我们面对的是 有 \(k-2\) 种颜色,每种颜色 \(k-1\) 或者 \(k\) 个,能否取出 \(k-2\) 个互不相交的区间这么一个问题。显然一种颜色有 \(k\) 个的情况肯定优于只有 \(k-1\) 个的情况,如果所有颜色的元素个数都只有 \(k-1\) 个命题仍然成立,那么其中一部分颜色的元素个数为 \(k\) 的命题同样成立。因此我们可以钦定所有颜色都只剩下了 \(k-1\) 个,发现这样子就成功将 \(Q(k-1,k)\to Q(k-2,k-1)\)。容易发现当 \(k=2\) 时,\(Q(k-1,k)\) 显然是成立的。因此 \(\forall k,Q(k-1,k)\) 均成立。
T694850 11.16 T2 - 基站修建(build)
考虑到整个矩形只有三行,所以肯定会有能用的性质。设两点分别为 \((x_1,y_1),(x_2,y_2)\),那么其距离的平方为 \((x_1-x_2)^2+(y_1-y_2)^2\)。而注意到 \((y_1-y_2)^2\in\{0,1,4\}\),而 \((x_1-x_2)\in \N\),因此当 \(x\) 坐标的差稍微增大一点的时候,距离的平方就会增大很多,而 \(y\) 坐标能起到的最大贡献只有 \(4\) ,是弥补不来的。
因此,比较两段距离的大小 几乎 可以只关注横坐标。也就是说,对于一个点,离他最近的点 几乎 就是离他最近的那一列的那些点;离他更远的那些列的点,几乎不可能距离这个点更近。
我们已经找到了非常良好的性质,即我们在加入新点的时候,几乎 只需要考虑之前已经加入的最靠后的那些点即可。通过这种方式,我们每加入一个点就能知道它到之前的点的最短距离是多少,而关键信息几乎只需要 上一个有点的列 的编号,因此很容易使用 dp 来直接求出答案。这个东西没必要使用 二分 转为判定性问题,否则凭空多一个 \(\log\) 且容易误导 dp 的设计方向(我赛时的时候就这么考虑二分的 check 该怎么写,每个点放入后都会覆盖掉一个半径为 d 的圆,在这个范围内不能放入新的点。但是这样从圆覆盖的角度思考实际上并没有很好的用到整个矩阵只有三行的性质,所以非常难思考,真不如直接 dp 求解)。
考虑到我们上面的讨论都带着一个 “几乎”。这是因为通过简单分析可知,当多个点位于同一个 \(9\times 9\) 的方阵内部时,两点间的最短距离并不能仅通过 \(x\) 坐标之差就很好地体现,比如下面这种情况:
1 . 3
. . .
. 2 .
如图,尽管 2 号点所在的列离 1 号所在的更近,但实际上是 3 号点到 1 的距离要小于 2 到 1。也就是说,在小范围中,我们纵坐标的信息是不能抛弃的。但是这样的特殊情况只存在于至多 \(9\times 9\) 的范围内,因此我们可以考虑 状压,只将当前列的状态和上一列的状态(类似炮兵阵地)压缩后存入 dp 的状态里面,这样子我们转移的时候就同样可以考虑到上述的这种特殊情况,而不会出问题。
具体的,设 \(f_{i,num,j,k}\) 表示考虑到第 \(i\) 列,一共放了 \(num\) 个点且在第 \(i\) 列至少放了一个点,第 \(i\) 列的状态为 \(j\) ,第 \(i-1\) 列的状态为 \(k\) 的答案(\(1\) 表示放了点 \(0\) 表示没放)。转移的话就考虑枚举上一个有点的列的位置 \(i_1\) 以及其对应两列的状态,然后更新最小距离的大小即可。
值得注意的是,这个正解的复杂度是 \(O(2^{12}\cdot n^3)\) 的,但因为基本上都是循环而且可以剪枝的地方挺多的,因此卡卡常就能过。
T694851 11.16 T3 - 双端队列(deque)
要求输出方案的 dp,要多用一个数组 \(g\) 来记录当前状态是从哪个状态转移过来的,\(g\) 数组在dp的过程中就可以很简单地处理好。然后输出方案就是倒着跳 \(g\) 即可,千万不要写复杂了,否则细节很多很难写。
除非有可以利用得上的性质,否则设计 dp 的时候不要把状态复杂化(赛时考虑了一下类似 CSP-S2024 t3 的一个状态设计思路,状态线性但是转移 \(O(n)\),能做但是明显不好优化。),不然很可能得不到可以优化的形式。
直接考虑最简单的状态设计:考虑了前 \(i\) 个数,那么左右两端恰好有一边是 \(a_i\),设另一端为 \(a_j\),且 \(a_i\) 在左/右边,这个状态的答案用 \(f_{i,j,0/1}\) 来表示。转移就直接考虑 \(f_{i-1,j,d}\to f_{i,j,d},~f_{j,i-1,!d}\to f_{i,i-1,d}\) 即可。输出方案就是对 dp 决策点的溯源。
此时应该考虑优化转移。常见 trick:我们发现每次转移都是由 \(f_{i-1,*,0/1}\to f_{i,*,0/1}\),于是一整轮的转移,就相当于一次序列变换。如果序列变换的方式比较简单(每次都是一个区间修改或者单点修改之类的)我们可以考虑用数据结构来维护这整个序列,就避免了每个点单步转移,实现了整体的转移。
发现形如 \(f_{i-1,j,d}\to f_{i,j,d}\) 这样的转移是非常自然的,因为其相当于 \(f_i\) 对应的序列是由 \(f_{i-1}\) 原封不动继承得到的,也就是说我们可以不对 \(f_{i-1}\) 进行任何修改操作即可得到 \(f_i\)。而对于 \(f_{j,i-1,!d}\to f_{i,i-1,d}\) ,相当于一个区间会贡献到一个点上。单点修改是容易的,考虑能否快速计算这一个区间的贡献呢?答案是否定的,转移的时候计算贡献的方式比较复杂(每个贡献都要跟 \(|a_i-a_j|\) 取 \(\max\)),并不好利用常见的方法优化(这东西没法用数据结构来做啊,不支持区间 max 修改加区间 min 查询,只能一遍遍枚举,复杂度降不下来)。
考虑限制我们优化的点就在于我们的 dp 数组存了具体的答案,而这个答案的更新并不好维护。考虑将最优化问题使用二分转为判定性问题,这样子我们的 dp 数组只需要存 0/1 即可不可行,因为最终答案已经被我们通过二分求出来了。考虑我们目前二分到的答案为 \(d\),那么转移就应该满足:
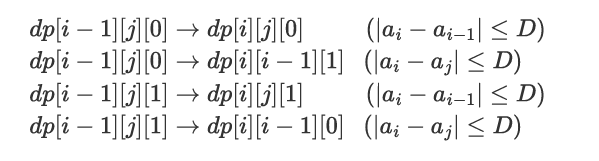
与原本不同的是,每条转移能否成立还得看是否满足后面的那个式子。可以发现能够对 \(i\) 产生贡献的位置 \(j\) 都有 \(a_i-d\le a_j\le a_i+d\),在值域上形成了一段连续的区间!那么这整个转移过程就可以被抽象为一段区间对单点产生了贡献,而我们需要维护的仅仅只是该区间内是否有 \(1\) 即可。这东西就非常好用线段树来维护了,至于方案输出只需要记录每个 dp 状态是由哪个转移得到的即可(要么是从 i-1 状态继承的,要么就是从某个 j 转移得到的,记录其中一个 j 即可)。
但其实我们只关心整个 \(f_i\) 序列中为 \(1\) 的那些位置, \(0\) 不会对整个转移产生任何影响。因此其实我们可以不用线段树维护整个序列,而仅仅用一个 set 来维护 dp 值为 \(1\) 的那些位置 \(j\) 所对应的 \(a_j\),这个 set 就是当前阶段整个 dp 序列的实际有效信息,转移的话就用 set.lower_bound 看一下在 set 里是否有在 \([a_i-d,a_i+d]\) 这个范围内的数,如果有说明这个位置可以贡献 \(1\) 给 \(f_{i,i-1,d}\) ,然后将 \(a_i\) 加入到对应 set 中即可。
set<pair<int,int>> 的 lower_bound 函数是对 first 进行查找,second 并不影响。故可以写为 s.lower_bound({x,-1});
堆支持删除操作,实现需要使用 懒删除:因为我们最终关心的一定是堆顶,如果堆顶没有被删除过那么哪怕有被删除过的数残留在堆中也不影响;如果堆顶被删除了,那么弹出该堆顶知道找到一个未被删除过的堆顶即可。
P9565 [SDCPC 2023] Not Another Path Query Problem
考虑如果直接模拟得到某条路径的值为 \(k\) 将其与 \(V\) 比较,这样子复杂度一定是降不下来的。可以考虑不关注具体 \(k\) 的值,而是将 \(k\) 按照二进制位拆分成 \(|S|\) 种组合,然后生成 \(|S|\) 张新图,使得新图上任意一条路径上的值一定大于 \(V\)。然后就变成了一个对 \(|S|\) 个图的连通性问题,可以用并查集解决。
容易发现 \(|S|=\log_2k\) 的方案是容易构造的。
P5524 [Ynoi2012] NOIP2015 充满了希望
在操作序列上进行的区间问题,考虑每个贡献的来源。发现每个贡献的来源并不随着查询区间的改变而改变,故可以预处理后离线回答询问。
多次询问,可以考虑扫面线离线处理其中一个端点,另一个端点的信息用数据结构维护。
对于每次加边,我们称将两个原本不联通的块变为联通的边是有效的,那么显然有效边的数量级是 \(O(nd)\)。
利用并查集判断两点是否联通,本质上是判断点 \(a\) 和 点 \(b\) 所在集合的代表元素 \(fa_a\) 和 \(fa_b\) 是否相同。每个点都在 \(d\) 张图中,那么其一定能用 \(fa_{1,a},fa_{2,a}\cdots fa_{d,a}\) 这么一个序列来刻画与其他点的联通关系。两点在多张图中均联通当且仅当描述这两个点的序列完全相等,这个可以用哈希来做。
因此我们只要能在可接受复杂度的情况下,在每次加边的时候维护每个点的 \(fa\) 序列,即可回答询问(用 map 可以轻松统计有多少个点每张图都在同一个联通快中)。
如何维护。考虑一次有效的连边,对应着将两个点集 合并,因此考虑启发式合并均摊复杂度,每次只需要遍历大小较小的那个集合的每一个点,修改其 \(fa\) 序列上对应位置即可。
考虑字符串哈希的本质:\(\sum\limits_{i}(B^i\cdot S_i)\),而 \(B_i\cdot S_i\) 本质上是一个关于 \(S_i\) 和 \(i\) 的函数,因此我们可以直接考虑用泛化的 \(W(i,S_i)\) 来替代原本哈希过程中的大常数乘法。\(W(i,S_i)\) 可以使用 mt19937_64 直接取随机数,提前存好调用即可。
对多个字符串的匹配问题,可以直接先尝试对这多个字符串建 trie 树,然后转为 树上游走 的问题。
此题中,病毒片段是一个正则表达式,是不固定的,因此我们没办法在 dna 串建出的 trie 树上单纯访问一条链就找到所有的匹配串。由于病毒串有多种可能,因此我们也应该优化我们的便利方式,运用支持访问多条路径的 dfs 来搜索 trie 树。用 状态 \((st,now)\) 表示现在已经匹配到病毒串的第 \(st\) 位,目前在 \(trie\) 的第 \(now\) 个节点上。
考虑当前状态的转移:若 \(a_{st}\in\{A,C,G,T\}\),那么直接移动到 \(now\) 对应的子节点中,\(st+1\to st\);若 \(a_{st}=?\) ,那么需要尝试遍历 \(now\) 的每个子节点,且 \(st+1\to st\);若 \(a_{st}=*\),则当前位可以匹配空串,即 \(st+1\to st\) 且 停留在 \(now\),或者 \(st\) 不变并遍历 \(now\) 的所有子节点。
可以发现这样子进行游走一定能找出所有匹配的串,但是复杂度无法保证。加一个记忆化即可,因为这个 dfs 游走时的状态简洁得就对应一种 dp。
推 dp 转移的时候一定要手玩一下所有情况,考虑准确。
变为 trie 树上用最小次数删除大小不超过 \(k\) 的子树的问题。容易想到设计 \(f_u\) 表示删除完 \(u\) 这个棵子树的答案,那么转移就是 \(f_u=1+\sum\limits_{v\in u}f_v\) 吗?并不是。因为每棵子树实际上并非相互独立,每个 \(v\) 都通过其父节点 \(u\) 联系在一起。也就是说,我们转移的时候,可以选择在 \(v_1,v_2\) 两颗子树中各自剩下一部分节点,然后选中 \(u\) 将其一次性删除。通过这样的操作,我们可以选择只用 \(f_v-1\) 次操作(显然只用 \(f_v-2\) 次操作一定会导致剩余的数 大于 \(k\),不能连同 \(u\) 一次性删完)来删除 \(v\) 子树而不是 \(f_v\)。我们应该选择出尽可能多的的子树,使其剩下一些节点随 \(u\) 一次性删除。
那么就考虑令维护一个 \(g_u\),表示在用 \(f_u\) 次操作删除完 \(u\) 这个子树的前提下,最后一次删除操作所删除的节点最少为 \(g_u\)。这样我们就可以对每个 \(v\) 让其留下 \(g_v\) 个节点随 \(u\) 一起删除。选择出最多的 \(v\) 贪心是简单的,只需要将 \(g_v\) 从小到大排序后,从小到大选最多个 \(g_v\) 使得 \(g_u=1+\sum\limits_{v}g_v\le k\) 即可。
另一种思路:我们每次删除的子树,一定可以是这整棵树中不超过 \(k\) 且最大的那棵(首先我们不可能在这颗子树内部找树删除。我们当然可以选择与这颗子树有相同祖先的其他子树删去,然后再通过将变小了的祖先删去来达到删除该子树的目的,但是这显然不优,因为我们的操作目的是使 祖先 尽可能快地变小,从而删除当前子树。而删除该 最大 子树恰恰是削弱祖先大小地最快方法。因此最优方案下我们一定会删除该子树。)于是我们维护这个贪心过程即可得到答案。
但是直接模拟这个过程不好实现代码,我们要进行转换。考虑刚才我们对该思路地证明中提及了,该方法能保证用最少地步数使得祖先的大小逐渐减小至不超过 \(k\)。那么我们就借此来正着实现代码,设计一个函数 solve(u) 表示将子树 \(u\) 的大小缩小至不超过 \(k\) 的最小步数。函数内部的实现则是:若 \(u\) 的所有子节点 \(v\) 的子树大小均不超过 \(k\) ,那么我们优先选择子树大小较大的 \(v\) 使用一次操作将其删除,直到 \(u\) 的大小不超过 \(k\);若 \(u\) 的子节点中存在大小超过 \(k\) 的,那就调用 solve(v) 先将其减至 \(k\)。
实现代码的时候考虑非平凡情况,在这题中就是当子树 \(u\) 的任意一个子节点 \(v\) 的大小均不超过 \(k\) 时,我们应该怎么删除。处理好这一步,发现平凡情况递归实现即可。
通过题目计算贡献的形式,容易想到固定左端点来处理比较方便(新加入一个数不会影响到前面的数的贡献)。由于贡献均为正数,故相同左端点的情况下,好的区间长度越短越好。
考虑如何对于每个左端点 \(l\) ,求出其对应最短好区间的右端点。直接按照题目定义通过模拟来找难以优化(每次向后延申一些位置,又会增加新的要求,不好处理,赛时在这里没处理好浪费了很多时间。)考虑将好区间所满足的条件列出来:\(lst_i\ge l,nxt_i\le r\),其中 \(i\) 表示 \([l,r]\) 内的某种颜色,\(lst_i\) 表示该颜色第一次在序列中出现的位置,\(nxt_i\) 表示最后一次出现的位置。
同时处理上述两条限制同样不好做,于是我们先分别处理单条限制,再寻找其交集令两条限制同时成立。只考虑 \(lst_i\ge l\) 是容易的,只需要保证在 \(l\) 左侧就已经出现过来的颜色不被纳入区间内即可,右端点的限制同理,这些都可以简单预处理出来。
将左右端点的限制组合起来,直接用二分查找即可:判断在满足 l 限制的位置是否有 r 也能让其满足 r 限制。
然后就能找出所有的好区间。发现对于每个区间没啥好办法可以快速计算贡献,于是转头分析好区间之间的关系。可以发现好区间要么相离要么包含,而被包含的好区间一定优于包含它的区间。于是实际上有效的好区间就是不交的了,直接扫一遍计算贡献即可。
法2:如果一看完题就分析好区间之间的位置关系,就能发现左右端点之间具有某种单调性,可以考虑双指针。
法 3:xor hash。由于我们要让某些颜色被完全包含进好区间中,不能有一个漏网之鱼,那么我们可以使用一些随机化相关的做法来快速判断一个区间内是否完整包含了某种颜色。考虑给每个位置 mt19937_64 一个随机权值,并保证 同种颜色的点的权值异或和为 \(0\)。那么一个区间是好的,的充分条件就是这个区间内点的异或和 为 \(0\),且几乎是充要的,错误概率很小。因此找好区间的问题就变成找异或和为 0 的区间的问题了,可以用前缀异或和和桶来实现。
先找基本性质:\(0\) 必须在 \(2\) 前面,\(1\) 必须在 \(3\) 前面,否则无解。\(0\) 的最大值小于 \(1\) 的最小值,\(2\) 的最大值小于 \(3\) 的最小值。然后就可以过特殊性质 AB 了。
考虑特殊性质 C 怎么写:排列计数,题目给出的限制均与元素相对大小有关,于是 dp 状态中存相对大小而不是绝对大小。设 \(f_{i,j}\) 表示前缀 \(i\) 已经满足限制,且第 \(i\) 位在前缀中的相对大小为 \(j\) 的方案数。那么对于 \(a_i=0\),只有一个转移 \(f_{i,1}=\sum\limits_k^{i-1}f_{i-1,k}\);若 \(a_i=3\) ,设 \(i\) 的前一个为 \(3\) 的位置是 \(lst_i\),那么我们使前缀 \(i\) 满足限制的充要条件为 \(a_{lst_i}<a_i\)。思考一下这为什么是充要的。由于我们 dp 状态仅记录了当前位置的相对大小,因此若 \(lst_i\) 在 \([1,lst_i]\) 中的相对大小为 \(k\),考虑到我们在 \(lst_i\) 后面还加入了 \(i-lst_i-1\) 个全局最小值,因此 \(lst_i\) 在 \([1,i-1]\) 中的相对大小实际上是 \(k+i-lst_i-1\)。因此此时我们的转移就应该是 \(f_{i,j}=\sum\limits_{k,k+i-lst_i-1<j}f_{lst_i,k}\) 。注意当 \(lst_i\) 不存在时 \(f_{i,j}=1\)。
惊人注意到将原序列的 \(1\to 0\),\(2\to 3\) ,然后使用 C 性质的代码即可通过。原因是,将性质替换后符合条件的排列和符合原限制的排列有双射关系,一一对应。
证明:对于一个极长的,仅包含 \(\{0,1\}\) 的前缀,我们任意交换 \(0\) 和 \(1\) 的位置,不改变答案(考虑对于原本合法的一个排列,交换了 \(0,1\) 位置后,将排列中对应位置也交换,得到的排列符合新的限制。此过程可逆,因此是双射)。那么我们不妨将这个极长的前缀排列成 \(000\cdots0111\cdots1\),根据我们一开始得到关于本题的性质,要么全部的 \(1\) 都在这,要么全部的 \(0\) 都在这了。只讨论全部的 \(0\) 都在前缀上的情况,我们可以把所有的 \(0\) 替换成 \(1\) ,方案数不变。因为 \(0\) 的最大值小于 \(1\) 的最小值。此时序列中就没有 \(0\) ,只有 \(1\) 了。继续考虑后缀,因为前面讨论了存在极长的前缀使得只有 \(\{0,1\}\) 且包含全部的 \(0\),那么就会有一个极长的后缀只有 \(\{2,3\}\) 且包含全部的 \(3\)。我们同样可以使用上述方式,在不改变方案数的情况下,使 \(3\) 全部换成 \(2\)。此时整个序列中只有 \(\{1,2\}\),发现只要将对应合法排列左右颠倒一下,就对应了序列中只有 \(\{0,3\}\) 的情况。经过上述过程,\(1\to 0,2\to 3\),且方案数不变,证毕。
方法 2: 考虑用另一种方式刻画排列的生成过程。设 \(p_i\) 表示排列 \(p\) 的第 \(i\) 个数。原先只有一个 \(p_1\),然后我们考虑插入 \(p_2\),可以插在 \(p_1\) 的左边表示 \(p_2<p_1\) 或者插入在 \(p_1\) 的右边表示 \(p_2>p_1\);然后插入 \(p_3\),可以插入在最左端,最右端或是 \(p_1,p_2\) 的中间,分别表示一种三个元素间的偏序关系。以此类推。通过模拟这个过程我们可以生成出任何排列 \(p\) ,且在该过程中,我们时刻关注两两元素之间的相对大小关系,这有助于我们设计 dp 状态来刻画有关相对大小限制的排列问题。
回到本题,我们使用上述方法来生成一个排列,并使其满足题目中的限制。若现在考虑插入 \(p_i\),且 \(op_i=0\) 那么 \(p_i\) 就要放在已完成部分的最左端(已完成部分就是 \(p_{1\cdots i-1}\),也就是前缀,他们都应该大于 \(p_i\));若 \(op_i=1\) ,同理应该将 \(p_i\) 插入到最右端。若 \(op_i=2\) ,表明应满足 \(p_i\) 是一个后缀最小值,那么此时插入 \(p_i\) 的位置就会受到限制:设 \(x\) 为上一个后缀最小值的位置,\(y\) 为上一个后缀最大值的位置,那么为了不破坏前面的限制,我们应保证 \(p_i\) 插入的位置在 \(p_x\) 的右端,且在 \(p_y\) 的左端。
考虑到这一步就会发现问题,如果我们直接将 \(x\) 和 \(y\) 设计进状态里面,那么无论怎么优化 dp 都只能是 \(O(n^3)\)。注意到 影响每一步转移的,其实并不是 \(x\) 或 \(y\) 具体的值,真正有意义的信息其实是 \(|x-y|\) ,也就是目前还剩多少个位置可以给 \(p_i\) 填。同理,填入 \(p_i\) 后对后面操作的影响,也只是 可填位置的个数 的变化。
因此,我们设计状态的时候不考虑分别记录 \(x,y\),而是 \(|x-y|\)。设 \(f_{i,j}\) 表示目前填到了 \(p_i\),对于\(op=2/3\) 的点能填的位置个数为 \(j\) 的方案数。考虑当 \(op=0/1\) 时的转移:有解的情况下,一定是 \(0\) 在 \(2\) 之前且 \(1\) 在 \(3\) 之前。那么说明我们放入 \(0\) 的时候,还从来没放过 \(2\),也就是说对于后面要填的数并没下界限制,所以新增一个 \(0\) 就相当于新增了一个可填位置。对 \(1\) 分析同理。所以此时有 \(f_{i,j}=f_{i-1,j-1}\)。若 \(op=2/3\),那么填入一个数就会新增一个可填位置,且消耗至少一个原本可以填的位置,那么转移就是 \(f_{i,j}=\sum\limits_{k\ge j}^{i}f_{i-1,k}\) 。容易用后缀和优化。
其实还有法 3:考虑对于 \({0,1}\) 的集合,\({2,3}\) 的集合,其内部的偏序关系是固定的。一定有 \(0_{\max}<1_{\min},2_{\max}<3_{\min}\)。于是将 \({0,1}\) 的集合视为序列 \(a\),\({2,3}\) 的集合视为序列 \(b\),那么我们实际上要做的就是往 a,b 两个序列内从小到大填入 \(1\cdots n\)。同时还得注意,往当前位置填入某个数的时候,看看会不会和已经填的部分产生冲突。这个操作容易用 dp 来计数。
状态是容易想到的,难点在于转移。对于这种 \(0,1\) 异或相关的序列问题,自由度比较大的话,一般都可以通过贪心导向一个比较简单的结论(重点关注 \(0\) 不会改变,\(1\) 可以逆转当前局面这一性质):如果所有子节点的子树大小均为偶数,那么显然局面是固定的,不需要贪心直接计算即可;如果存在一个大小为奇数的子节点,那么可以贪心发现,所有偶数大小的子节点的最优状态一定是可以取到的,直接取走即可。那么剩下只需要考虑所有子树大小为奇数的子节点,发现局面几乎也是固定的,形成 $0,1,0,1,\cdots $的交错序列。
对于这种交错的选取,可以维护两个分别代表 \(0\) 集合和 \(1\) 集合的序列向归并一样贪心地取,能做,但有更简单的写法。注意到子树只要 \(0,1\) 确定了,那么选取的顺序是无关的,也就是说我们可以理解为先将所有 \(1\) 取完,再将所有 \(0\) 取完。 \(0\) 和 \(1\) 分别要取多少个我们可以通过简单计算得到。那么我们就可以先所有子节点都认为选 0,然后再挑出所需要的,增量最大的那几个子节点将他们改为 1即可。
将概率转化为计数。\(m\) 特别小,提示应该是指数级做法,考虑 状压 dp 或者 容斥(枚举子集)。
考虑在所有合法局面中,玩具 \(i\) 在 \(A_i\) 种局面中成为残次品。那么每个 \(i\) 的坏掉的概率实则只跟 \(A_i\) 有关,那么就变成了一个计数问题。现在统计钦定 \(i\) 是坏掉的,那么一共有多少种合法局面(每组抽样中至少有一个坏掉)。对于这种要求每条限制都成立,且成立的方案不好计数,但 不成立 的方案容易统计的时候,考虑容斥 。显然当 \(i\) 坏掉了,那么所有覆盖了 \(i\) 的抽样一定都被满足了。对于不包含 \(i\) 的一份抽样,设他包含了 \(T\) 个元素,那么此时该组不满足限制的情况数是 \(2^{n-T-1}\)(\(T\) 个元素都没坏,第 \(i\) 个元素坏了,剩下任意)。然后经典枚举子集乘上容斥系数计算即可。
考虑套一个高精度来实现最后的方案数比较大小。
注意正确计算时间复杂度,\(O(\frac{n}{\omega})\) 即使当成常数在 \(n=2000\) 时也有 \(30\) 左右,肯定 T 飞。要实现 变量分离,也就是提前预处理,不要把能提前预处理并存储起来的东西,放进核心代码里每次决策都重新算一次。
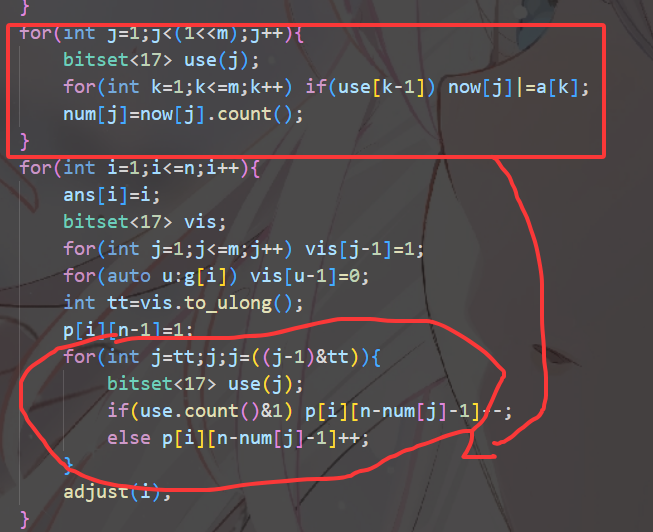
不要把红色框内能够预处理的部分,每次都放在圆圈内现场计算。
T700723 11.23 T3 - 简单树上求和问题(sum)
如果不消掉那个平方,直接做怎么做都要枚举 \(i,j\) ,且没办法用启发式合并等方法均摊复杂度。于是考虑将平方拆掉,将贡献均摊到每个二进制位上:\(x^2=\sum\limits_{i,j}(x_{(i)}=x_{(j)}=1)2^{i+j}\),其中 \(x_{(i)}\) 表示二进制表示下 \(x\) 的第 \(i\) 位。
那么将平方转为了在二进制位上的运算,异或同样也是按位来运算的,两者就可以结合了。\((a_i\oplus a_j)^2=\sum\limits_{x,y}2^{x+y}(a_{i_{(x)}}\oplus a_{j_{(x)}}=a_{i_{(y)}}\oplus a_{j_{(y)}}=1)\)。将答案拆成这样的好处就是,我们不同 \(i,j\) 的概念被模糊化了,也就是说我们只考虑当前的二进制位下 整个序列的性状,而不是单独一对 (i,j) 的性状。因此我们原本 \(O(n^2)\) 枚举 \(i,j\) 的过程被优化为了只需要 \(O(\log^2 n)\) 地枚举两个二进制位。
只考虑二进制位的话,问题就转为了,对多个询问节点,子树内距离不超过 \(d\) 的,满足某种要求的点进行计数。这东西看起来很像 dsu on tree 但实际上不好做且常数还大。考虑将树上距离转为跟深度有关的信息。那么对于 \(u\) 子树内距离 \(u\) 不大于 \(d\) 的点集,就满足 \(v\in S_u\) 且 \(dep_v-dep_u\le d\to dep_v\le d+dep_u\),同理“子树内”这个条件是可以用 dfs 序来表示的,因此实际上限制就是 \((L_u\le dfn_v\le R_u,dep_v\le dep_u+d )\),这种二维偏序问题显然可以考虑做二维数点:通过排序按顺序枚举的方式消掉一个维度,再通过权值上建立数据结构消掉另一个维度。
具体的,我们离线询问,将询问按照 \(d+dep_u\) 从小到大排序(是的我们实际上是分离了变量),再按照深度从小到大枚举节点并用一棵 bit 维护 dfn 序列上的信息,统计的时候查询 \([L_u,R_u]\) 区间上的答案即可。
分离变量是一个常见的思路,具体实现方式有:对不等式进行移项(T700723 11.23 T3 - 简单树上求和问题(sum),将距离转为 深度 的偏序关系 P1600 [NOIP 2016 提高组] 天天爱跑步),改变枚举的东西(横向求和转为纵向求和,类似于交换求和顺序,比如按二进制位来统计贡献,如T700722 11.23 T2 - 玩具质检(toy)),亦或是分类讨论(例如讨论贡献是从哪里来的,如 P6647 [CCC 2019] Tourism,T647135 「不可知域」)。同时多个限制也可以先分离,再合并,其过程类似二维数点(先通过排序消掉一维限制,再在此基础上用数据结构维护另一维),以及 P14567 【MX-S12-T2】区间 的第一种方法。
对于选取物品个数有 \(\le\) 限制计数,一般不好做,那么尝试将其容斥,转为对 \(\ge\) 的限制进行计数。由于选取的下界确定,我们可以钦定一部分是必选的,剩下的部分是任意选的。也就是说 \(\ge\) 会比 \(\le\) 更容易计数。
对于 至少包含一个 这种限制,同样考虑容斥改为一个都不包含,更好做。
观察题目是否有小量,考虑指数容斥。
动态过程离线处理,可以方便得到全局信息。T649737 R9 - B. 万物有灵
一定选 or 一定不选 比 至少至多 更好处理,考虑容斥转换。P13662 「TPOI-5A」Luminescence
巧妙利用模拟来解决一些难以处理的环节。Gellyfish and Camellia Japonica AT_arc130_c [ARC130C] Digit Sum Minimization P12976 受力分析 Force
多个限制可以考虑分别处理,最后再将其组合。
AT_abc391_f [ABC391F] K-th Largest Triplet
直接加入后继的话,可能会出现 重复状态


 浙公网安备 33010602011771号
浙公网安备 33010602011771号