Datawhale X 李宏毅苹果书AI夏令营深度学习进阶(一)

一.深度学习定义和核心

1.1 局部极小值与鞍点

我们在做优化的时候经常会发现，随着参数不断更新，训练的损失不会再下降, 但是我们对这个损失仍然不满意。把深层网络（deep network）、线性模型和浅层网络（shallow network）做比较，可以发现深层网络没有做得更好——深层网络没有发挥出它完整的力量，所以优化是有问题的。但有时候，模型一开始就训练不起来，不管我们怎么更新参数，损失都降不下去。这个时候到底发生了什么事情？

1.1.1 临界点及其种类过去常见的一个猜想是我们优化到某个地方，这个地方参数对损失的微分为零，如图所示两条曲线对应两个神经网络训练的过程。当参数对损失微分为零的时候，梯度下降就不能再更新参数了，训练就停下来了，损失不再下降了。

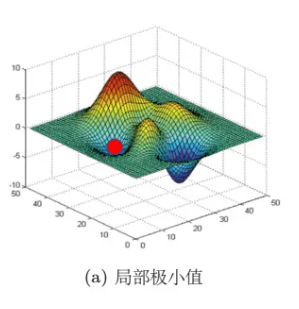
提到梯度为零的时候，大家最先想到的可能就是局部极小值（local minimum），如图所示。

所以经常有人说，做深度学习时使用梯度下降会收敛在局部极小值，梯度下降不起作用。但其实损失不是只在局部极小值的梯度是零，还有其他可能会让梯度是零的点，比如鞍点（saddle point）。鞍点其实就是梯度是零且区别于局部极小值和局部极大值（localmaximum）的点。

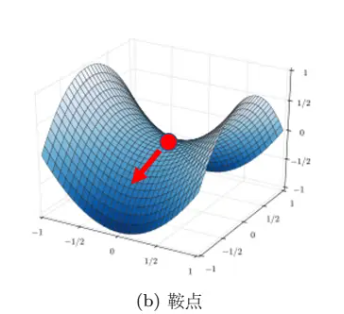
如图，红色的点在 y 轴方向是比较高的，在 x 轴方向是比较低的，这就是一个鞍点。鞍点的叫法是因为其形状像马鞍。鞍点的梯度为零，但它不是局部极小值。我们把梯度为零的点统称为临界点（critical point）。损失没有办法再下降，也许是因为收敛在了临界点，但不一定收敛在局部极小值，因为鞍点也是梯度为零的点。但是如果一个点的梯度真的很接近零，我们走到临界点的时候，这个临界点到底是局部极小值还是鞍点，是一个值得去探讨的问题。因为如果损失收敛在局部极小值，我们所在的位置已经是损失最低的点了，往四周走损失都会比较高，就没有路可以走了。但鞍点没有这个问题，旁边还是有路可以让损失更低的。只要逃离鞍点，就有可能让损失更低。

一个简单的神经网络，它只有两个神经元，而且这个神经元还没有激活函数和偏置。输入 x，x 乘上 w1 以后输出，然后再乘上 w2，接着再输出，最终得到的数据就是 y。

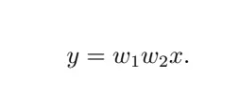
一个简单的训练数据集，这个数据集只有一组数据 (1,1)，也就是 x = 1 的标签是 1. 所以输入 1 进去，我们希望最终的输出跟 1 越接近越好

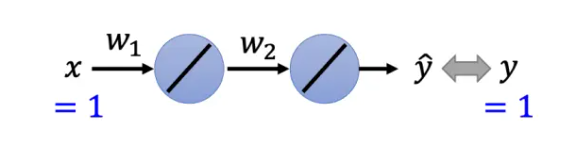
多数的时候，我们训练到一个梯度很小的地方，参数不再更新，往往只是遇到了鞍点。

2.1批量和动量

实际上在计算梯度的时候，并不是对所有数据的损失 L 计算梯度，而是把所有的数据分成一个一个的批量（batch）遍历所有批量的过程称为一个回合（epoch）。事实上，在把数据分为批量的时候，我们还会进行随机打乱（shuffle）。随机打乱有很多不同的做法，一个常见的做法是在每一个回合开始之前重新划分批量，也就是说，每个回合的批量的数据都不一样。

实际上，批量梯度下降并没有“划分批量”：要把所有的数据都看过一遍，才能够更新一次参数，因此其每次迭代的计算量大。但相比随机梯度下降，批量梯度下降每次更新更稳定、更准确。随机梯度下降的梯度上引入了随机噪声，因此在非凸优化问题中，其相比批量梯度下降更容易逃离局部最小值。实际上，考虑并行运算，批量梯度下降花费的时间不一定更长；对于比较大的批量，计算损失和梯度花费的时间不一定比使用小批量的计算时间长 。

其实小的批量也对测试有帮助。假设有一些方法（比如调大的批量的学习率）可以把大的批量跟小的批量训练得一样好。实验结果发现小的批量在测试的时候会是比较好的

大的批量大小会让我们倾向于走到“峡谷”里面，而小的批量大小倾向于让我们走到“盆地”里面。小的批量有很多的损失，其更新方向比较随机，其每次更新的方向都不太一样。即使“峡谷”非常窄，它也可以跳出去，之后如果有一个非常宽的“盆地”，它才会停下来。

2.1.1动量法

动量法（momentum method）是另外一个可以对抗鞍点或局部最小值的方法。如图 3.14所示，假设误差表面就是真正的斜坡，参数是一个球，把球从斜坡上滚下来，如果使用梯度下降，球走到局部最小值或鞍点就停住了。 但是在物理的世界里，一个球如果从高处滚下来，就算滚到鞍点或鞍点，因为惯性的关系它还是会继续往前走。如果球的动量足够大，其甚至翻过小坡继续往前走。 因此在物理的世界里面，一个球从高处滚下来的时候，它并不一定会被鞍点或局部最小值卡住，如果将其应用到梯度下降中，这就是动量。

3.1自适应学习率

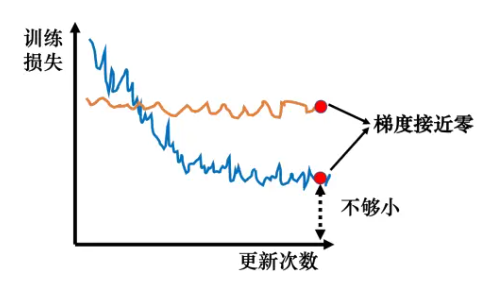
临界点其实不一定是在训练一个网络的时候会遇到的最大的障碍。图 3.18 中的横坐标代表参数更新的次数，竖坐标表示损失。一般在训练一个网络的时候，损失原来很大，随着参数不断的更新，损失会越来越小，最后就卡住了，损失不再下降。当我们走到临界点的时候，意味着梯度非常小，但损失不再下降的时候，梯度并没有真的变得很