线段树优化建图学习笔记

线段树 & 图

模版题

题意简述：给你 \(Q\) 个操作，这些操作包括三种：

• \(u\)，\(v\) 连有向边
• \(u\) 和 \([l,r]\) 里的所有点连有向边
• \([l,r]\) 中所有点向 \(u\) 连边

要求从 \(s\) 到所有点的最短路

暴力连边肯定是不可能的，观察操作，发现第一个可以直接完成，第二个第三个都是与区间有关的，想到区间就可以将其与线段树联系起来了。

优化建图

考虑一下可不可以在连区间的时候像线段树修改那样连到所有包含于区间内的区间，显然直接这样做是不可以的，因为区间节点和那些原本的节点是没有连接的，即使连了区间也无法连到区间内的点。

可是转念一想，没有连接或许并不是问题，没有连接我们是不是可以连上呢。先考虑操作二，向区间连边，连到区间点后，我们需要保证有一条长度为 \(0\) 的路径到达叶子点，于是我们在初始化的时候就可以将线段树每个节点向其儿子节点连条长度为 \(0\) 的节点。

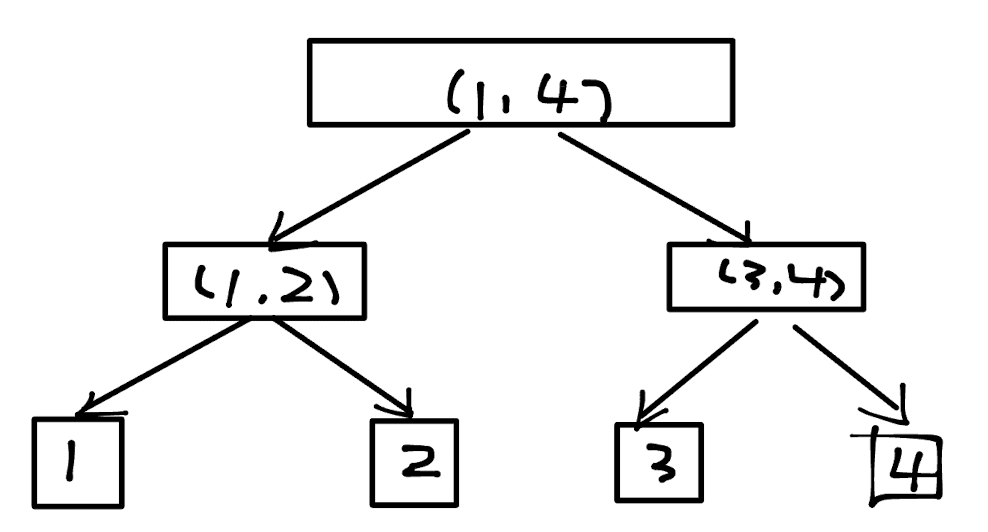
这样建树后，点连区间就变成了点连 \(log_2n\) 个代表区间的线段树节点了。

同样的，当做操作三的时候也需要一棵线段树，不一样的是这个线段树的节点由儿子指向父亲，其他都一样。

实现

在真实实现中，由于叶子节点都是一个点，用两棵树一个编号即可，其余的每个区间一个编号，连的时候直接从叶子中的点连上来。

//
//  线段树优化建图.cpp
//  
//  CF 786 B
//  Created by   on 2024/9/26.
//

#include <stdio.h>
#include <iostream>
#include <cstring>
#include <vector>
#include <queue>
#include <algorithm>

using namespace std;

const int N = 1e5+21;
#define lchild(x) x<<1
#define rchild(x) x<<1|1
typedef struct{
    int to;
    int nxt;
    int w;
}Edge;
Edge edge[N<<5];
int head[N<<3];
int cnt;
inline void add_edge(int u, int v, int w){
    edge[cnt].to = v;
    edge[cnt].nxt = head[u];
    edge[cnt].w = w;
    head[u] = cnt++;
    return;
}
int tree[2][N<<2];  //每个点的编号
int tot;
inline void build(int p, int pl, int pr){
    if(pl == pr){
        tree[0][p] = pl;
        tree[1][p] = pr;
        return;
    }
    int mid = (pl+pr) >> 1;
    tree[0][p] = ++tot;
    tree[1][p] = ++tot;
    build(lchild(p), pl, mid);
    build(rchild(p), mid+1, pr);
    add_edge(tree[0][p], tree[0][lchild(p)], 0);    //父亲连向儿子
    add_edge(tree[0][p], tree[0][rchild(p)], 0);
    add_edge(tree[1][lchild(p)], tree[1][p], 0);    //儿子连向父亲
    add_edge(tree[1][rchild(p)], tree[1][p], 0);
    return;
}
inline void update_in(int p, int pl, int pr, int l, int r, int x, int w){
    if(l <= pl && pr <= r){
        add_edge(x, tree[0][p], w);
        return;
    }
    int mid = (pl+pr) >> 1;
    if(l <= mid)
        update_in(lchild(p), pl, mid, l, r, x, w);
    if(mid < r)
        update_in(rchild(p), mid+1, pr, l, r, x, w);
    return;
}
inline void update_out(int p, int pl, int pr, int l, int r, int x, int w){
    if(l <= pl && pr <= r){
        add_edge(tree[1][p], x, w);
        return;
    }
    int mid = (pl+pr) >> 1;
    if(l <= mid)
        update_out(lchild(p), pl, mid, l, r, x, w);
    if(mid < r)
        update_out(rchild(p), mid+1, pr, l, r, x, w);
    return;
}
int n;
#define PII pair<long long, int>
priority_queue<PII, vector<PII>, greater<PII> >q;
long long dis[N<<3];
bool vis[N<<3];
inline void dijstra(int st){
    memset(dis, 0x3f, sizeof(dis));
    dis[st] = 0ll;
    q.push(make_pair(dis[st], st));
    while(!q.empty()){
        int x = q.top().second;
        q.pop();
        if(vis[x])
            continue;
        vis[x] = true;
        for(int i = head[x]; ~i; i = edge[i].nxt)
            if(dis[edge[i].to] > dis[x]+edge[i].w){
                dis[edge[i].to] = dis[x]+edge[i].w*1ll;
                q.push(make_pair(dis[edge[i].to], edge[i].to));
            }
    }
    for(int i = 1; i <= n; i++)
        if(dis[i] == dis[0])
            dis[i] = -1;
    return;
}
int main(){
    memset(head, -1, sizeof(head));
    int q, s;
    cin >> n >> q >> s;
    tot = n;
    build(1, 1, n);
    
    while(q--){
        int op;
        cin >> op;
        if(op == 1){
            int u, v, w;
            cin >> u >> v >> w;
            add_edge(u, v, w);
        }
        if(op == 2){
            int x, l, r, w;
            cin >> x >> l >> r >> w;
            update_in(1, 1, n, l, r, x, w);
        }
        if(op == 3){
            int x, l, r, w;
            cin >> x >> l >> r >> w;
            update_out(1, 1, n, l, r, x, w);
        }
    }
    dijstra(s);
    for(int i = 1; i <= n; i++)
        cout << dis[i] << ' ';
    return 0;
}