扫描线学习笔记

前置算法/数据结构

• 线段树
• 离散化

模版题

扫描线模板题

这道题要我们去求所有长方形的面积并，很显然这是一个二维问题，我们可以先从一维开始，再类比到二维问题上。

在求线段并的时候，一个很好想到的方法是利用线段树，每次加入线段时直接在线段树里标记一下即可，然后统计一下线段树里有几个地方被标记了就得出来答案。

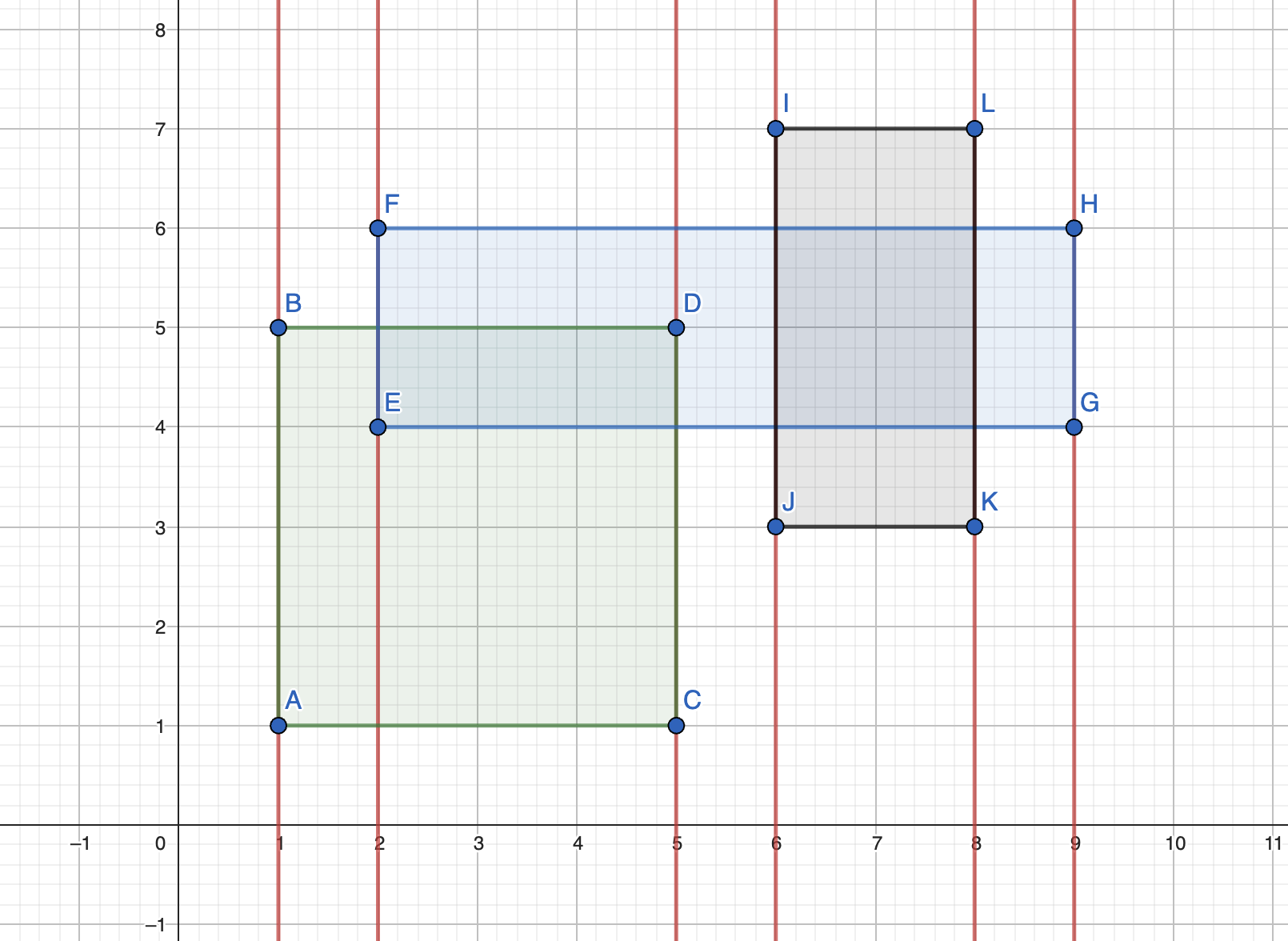
当类比二维的时候，不妨考虑一下图形的特殊性，长方形可以分解为很多个长为 \(h\)，宽一个单位长度的长方形。因为它为一个单位长度，我们可以将其视为线段，面积数值和线段长度数值是一样的，求长方形面积并就成了若干一维的线段并了。

然而，很明显，这样的一种方法是无法在规定时间内完成任务的，因此可以想到一种优化：离散化。

通过一些观察可以发现，这一条一条的“线段”会在一段区间内保持一样长，不妨设想是否可以合并这些条，答案是肯定的，我们将每个长方形的左右边界离散化，将线段并求出后求出两端之间的长度，将所有的加起来就是答案。

代码

#include <iostream>
#include <cstring>
#include <vector>
#include <unordered_map>
#include <algorithm>

using namespace std;

#define int long long
const int N = 1e6+35;
int n, lim;
typedef struct Scan_Line{
    int l, r, h;
    int mark;
    friend bool operator < (Scan_Line a, Scan_Line b){
        return a.h < b.h;
    }
    Scan_Line(int l, int r, int h, int mark):l(l),r(r),h(h),mark(mark){}
}Scan_Line;
vector<Scan_Line>v;
int X[N<<1];
unordered_map<int, int>mp;
class Segment_Tree{
private:
    typedef struct{
        int len;
        int cnt;
        int sum;
    }Tree_Node;
    Tree_Node tree[N<<3];
    inline int lchild(int x){return x<<1;}
    inline int rchild(int x){return x<<1|1;}
    inline void build(int p, int pl, int pr){
        tree[p].sum = 0;
        if(pl == pr){
            tree[p].len = X[pr+1]-X[pl];
            return;
        }
        int mid = (pl+pr) >> 1;
        build(lchild(p), pl, mid);
        build(rchild(p), mid+1, pr);
        tree[p].len = tree[lchild(p)].len + tree[rchild(p)].len;
        return;
    }
    inline void push_up(int p){
        if(!tree[p].cnt)
            tree[p].sum = tree[lchild(p)].sum + tree[rchild(p)].sum;
        else
            tree[p].sum = tree[p].len;
    }
    inline void modify(int p, int pl, int pr, int l, int r, int v){
        if(pl >= l && pr <= r){
            tree[p].cnt += v;
            push_up(p);
            return;
        }
        int mid = (pl+pr) >> 1;
        if(mid >= l)
            modify(lchild(p), pl, mid, l, r, v);
        if(mid < r)
            modify(rchild(p), mid+1, pr, l, r, v);
        push_up(p);
        return;
    }
public:
    inline void build(){
        build(1, 1, lim-1);
    }
    inline void modify(int l, int r, int v){
        modify(1, 1, lim-1, l, r-1, v);
    }
    inline int size(){
        return tree[1].sum;
    }
};
Segment_Tree tree;
inline void init(){
    cin >> n;
    for(int i = 1; i <= n; i++){
        int x1, y1, x2, y2;
        cin >> x1 >> y1 >> x2 >> y2;
        X[i*2-1] = x1;
        X[i*2] = x2;
        v.push_back(Scan_Line(x1, x2, y1, 1));
        v.push_back(Scan_Line(x1, x2, y2, -1));
    }
    n <<= 1;
    sort(v.begin(), v.end());
    sort(X+1, X+1+n);
    lim = unique(X+1, X+1+n)-X-1;
    for(int i = 1; i <= lim; i++)
        mp[X[i]] = i;
    for(auto &i : v)
        i.l = mp[i.l], i.r = mp[i.r];
    tree.build();
}
inline int calc(){
    int ans = 0;
    for(auto cur = v.begin(); cur != v.end()-1; cur++){
        auto nxt = cur+1;
        tree.modify(cur->l, cur->r, cur->mark);
        ans += tree.size()*(nxt->h-cur->h);
    }
    return ans;
}
signed main(){
    init();
    cout << calc() << endl;
    return 0;
}