树链剖分学习笔记
前置知识 Before
背景 Background
模版题传送门
在解决树上问题时,大部分时候暴力是会超时的,例如求两点间路径上的点权和。而树连剖分这个算法就可以让这种问题在 \(O(log(log(N)))\) 的。
树连剖分介绍 Intro
树链剖分分为重链剖分和长链剖分,但通常情况下说到树连剖分一般是指重链剖分。树连剖分的核心思路就是将一个树分为若干条链以达到快速修改和查询的目的。
概念 Concepts
- 重儿子:儿子中子树最大的
- 轻儿子:任何不是重儿子的儿子
- 重边:连接一个点和其重儿子的边
- 轻边:连接一个点和其轻儿子的边
- 重链:一条有重边组成的链
重链剖分 Heavy-Light Decomposition
重链剖分以子树大小为比较规则,每次把最“重”的儿子加入链中,以下是一个剖分的例子:(图中蓝色数字为子树大小。
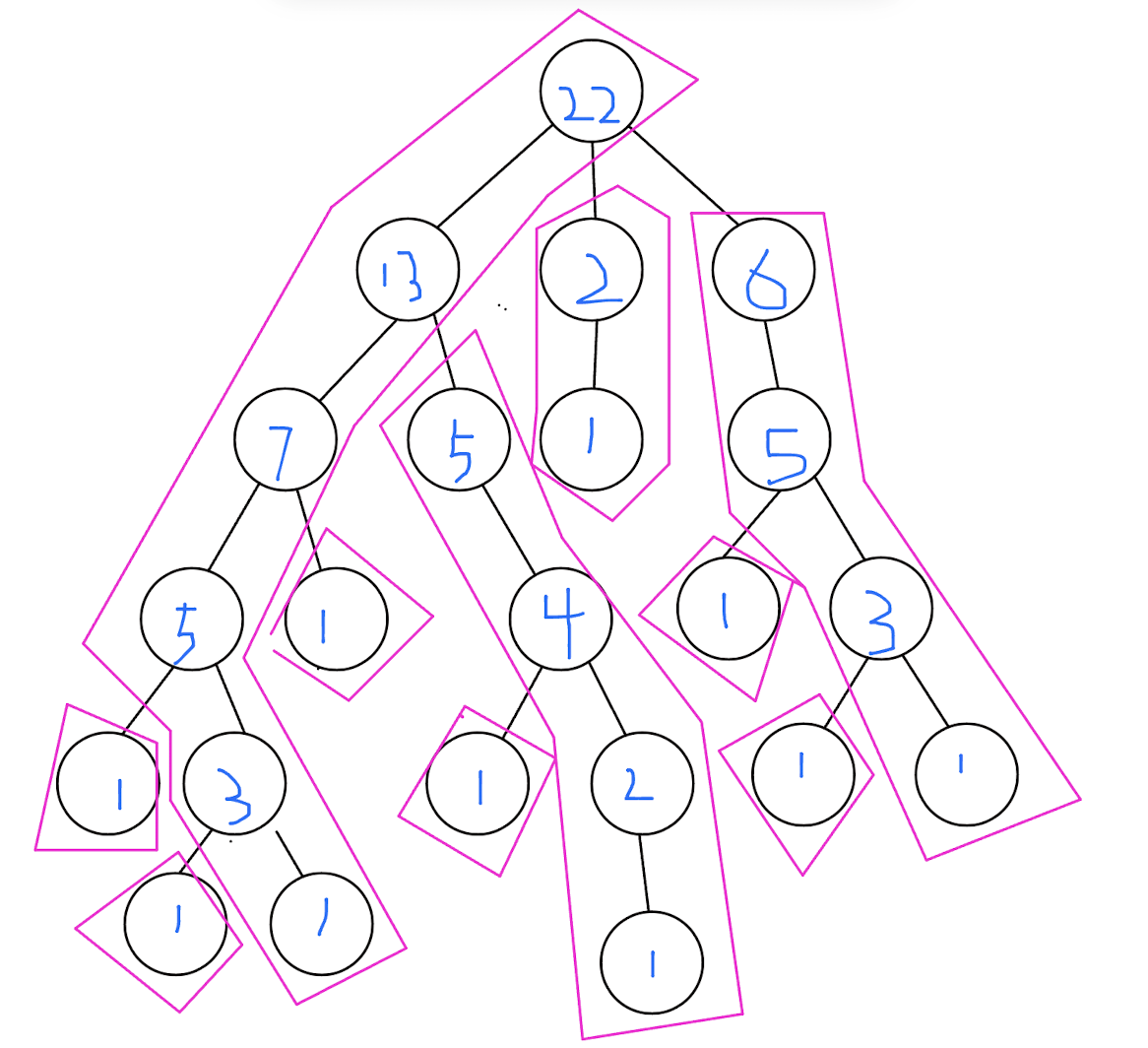
而我们如图中分出的重链能够连续,因此需要对他重新排序。给每个点计算 \(dfn\) ,在 dfs 过程中有限访问重儿子即可。同时需要记录每个点所在的重链的顶端 \(top_x\) 。
完成这些操作后大致可以得到下面的一种编号:
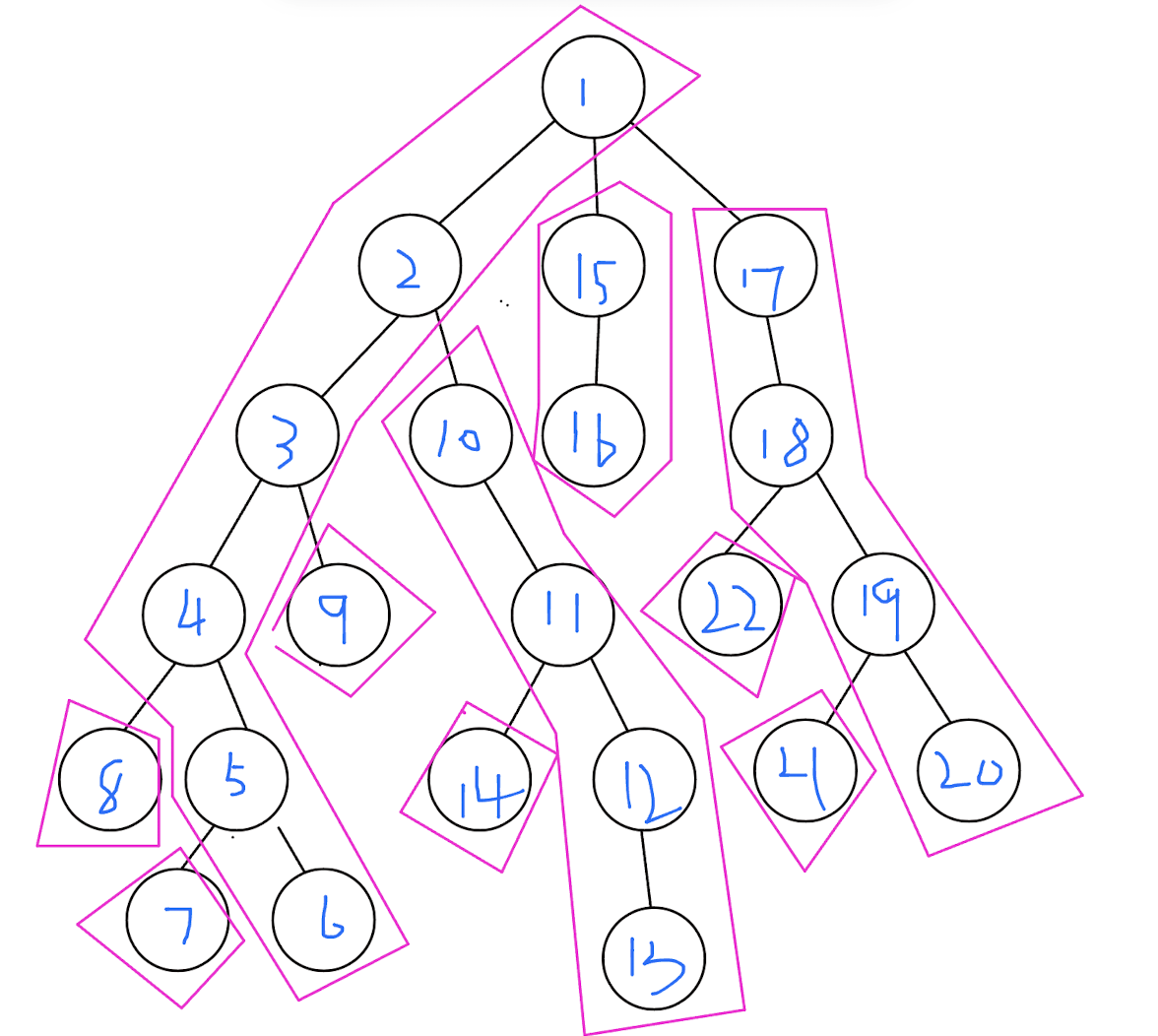
看到一个一个点区间,想到用一棵资瓷区间加区间查的线段树维护每个点的值。
各种操作/询问 Operations & Queries
子树的加法和询问是相当的简单,运用一个点子树内的 \(dfn\) 都是在一个特定区间内这一性质轻松解决。
至于路径上的修改和查询可以通过在重链上“跳”来实现。一种比较简单的实现方式是计算和修改一个点到根节点路径上的信息以计算或修改一段路径(这里要用到一点点 LCA )。
每次都查询/修改这个点到它的 \(top\) 的信息,然后再跳到 \(top\) 的父节点,重复操作即可。不难发现,因为轻边向上跳了以后,所在点的子树大小至少翻倍,所以大概有 \(log_2N\) 个轻边,那相应的有 \(log_2N\) 条重链,加上线段树的复杂度就是 \(log_2log_2N\) ,可以通过本题。
逮马🐎 CODE
//
// 树连剖分.cpp
//
// P3384 【模板】重链剖分/树链剖分
// Created by HurryCine on 2024/8/11.
//
#include <stdio.h>
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
#define int long long
const int N = 1e6+2;
int n, m, rt;
int mod;
int oval[N];
typedef struct{
int to;
int nxt;
}Edge;
Edge edge[N<<1];
int head[N];
int cnt;
inline void add_edge(int u, int v){
edge[cnt].to = v;
edge[cnt].nxt = head[u];
head[u] = cnt++;
}
int dep[N];
int fa[N];
int hson[N]; //重儿子
int siz[N];
inline void dfs1(int x, int Fa){
dep[x] = dep[Fa]+1;
fa[x] = Fa;
siz[x] = 1;
for(int i = head[x]; ~i; i = edge[i].nxt)
if(edge[i].to != fa[x]){
dfs1(edge[i].to, x);
siz[x] += siz[edge[i].to];
if(siz[hson[x]] < siz[edge[i].to])
hson[x] = edge[i].to;
}
return;
}
int dfn[N];
int val[N]; //dfn 对应的值
int top[N]; //重链顶端
int lst[N];
inline void dfs2(int x, int tp){
if(!x)
return;
dfn[x] = ++cnt;
val[cnt] = oval[x];
top[x] = tp;
dfs2(hson[x], tp);
for(int i = head[x]; ~i; i = edge[i].nxt)
if(edge[i].to != hson[x] && edge[i].to != fa[x])
dfs2(edge[i].to, edge[i].to);
lst[x] = cnt;
return;
}
namespace LCA{
int dep[N];
int eu[N<<1];
int idx[N];
int lst[N];
inline void dfs(int x){
eu[++cnt] = x;
idx[x] = cnt;
dep[cnt] = dep[idx[fa[x]]] + 1;
for(int i = head[x]; ~i; i = edge[i].nxt)
if(edge[i].to != fa[x]){
dfs(edge[i].to);
eu[++cnt] = x;
dep[cnt] = dep[idx[x]];
}
lst[x] = cnt;
return;
}
int lg[N<<1];
int dp[30][N<<1];
inline int get_a(int x, int y){
return dep[x] > dep[y] ? y : x;
}
inline void init_ST(){
for(int i = 1; i <= cnt; i++)
lg[i] = lg[i-1] + ((1<<lg[i-1]) == i);
for(int i = 1; i <= cnt; i++)
dp[0][i] = i;
for(int i = 1; (1<<i) <= cnt; i++)
for(int l = 1; l+(1<<i)-1 <= cnt; l++){
int r = l+(1<<i)-1;
int mid = (l+r) >> 1;
dp[i][l] = get_a(dp[i-1][l], dp[i-1][mid+1]);
}
return;
}
inline int lca(int x, int y){
int l = min(idx[x], idx[y]);
int r = max(idx[x], idx[y]);
int len = lg[r-l+1]-1;
return eu[get_a(dp[len][l], dp[len][r-(1<<len)+1])];
}
};
class Segment_Tree{
private:
int tree[N<<2];
int tag[N<<2];
inline int lchild(int x){return x<<1;}
inline int rchild(int x){return x<<1|1;}
inline void push_up(int p){
tree[p] = (tree[lchild(p)] + tree[rchild(p)]) % mod;
return;
}
inline void build(int p, int pl, int pr){
if(pl == pr){
tree[p] = val[pl];
return;
}
int mid = (pl+pr) >> 1;
build(lchild(p), pl, mid);
build(rchild(p), mid+1, pr);
push_up(p);
}
inline void add_tag(int p, int pl, int pr, int v){
(tree[p] += (pr-pl+1)*v % mod) %= mod;
(tag[p] += v) %= mod;
return;
}
inline void push_down(int p, int pl, int pr){
if(tag[p]){
int mid = (pl+pr) >> 1;
add_tag(lchild(p), pl, mid, tag[p]);
add_tag(rchild(p), mid+1, pr, tag[p]);
tag[p] = 0;
}
}
inline void modify(int p, int pl, int pr, int l, int r, int v){
if(l <= pl && pr <= r){
add_tag(p, pl, pr, v);
return;
}
push_down(p, pl, pr);
int mid = (pl+pr) >> 1;
if(l <= mid)
modify(lchild(p), pl, mid, l, r, v);
if(mid < r)
modify(rchild(p), mid+1, pr, l, r, v);
push_up(p);
}
inline int query(int p, int pl, int pr, int l, int r){
if(l <= pl && pr <= r)
return tree[p];
int mid = (pl+pr) >> 1;
int ret = 0;
push_down(p, pl, pr);
if(l <= mid)
(ret += query(lchild(p), pl, mid, l, r)) %= mod;
if(mid < r)
(ret += query(rchild(p), mid+1, pr, l, r)) %= mod;
return ret;
}
public:
inline void modify(int l, int r, int x){modify(1, 1, n, l, r, x);}
inline int query(int l, int r){return query(1, 1, n, l, r);}
inline void build(){build(1, 1, n);}
};
Segment_Tree tree;
inline void modify_subtree(int x, int v){
tree.modify(dfn[x], lst[x], v);
return;
}
inline int query_subtree(int x){
return tree.query(dfn[x], lst[x]);
}
inline void modify_up(int x, int v){
while(x){
tree.modify(dfn[top[x]], dfn[x], v);
x = fa[top[x]];
}
return;
}
inline void modify_path(int x, int y, int v){
modify_up(x, v);
modify_up(y, v);
int lca = LCA::lca(x, y);
modify_up(fa[lca], 10*mod-v);
modify_up(lca, 10*mod-v);
return;
}
inline int query_up(int x){
int ret = 0;
while(x){
ret += tree.query(dfn[top[x]], dfn[x]);
x = fa[top[x]];
}
return ret;
}
inline int query_path(int x, int y){
int ret = query_up(x) + query_up(y);
int lca = LCA::lca(x, y);
ret -= (query_up(lca) + query_up(fa[lca])) % mod;
return (ret+10*mod) % mod;
}
signed main(){
memset(head, -1, sizeof(head));
cin >> n >> m >> rt >> mod;
for(int i = 1; i <= n; i++){
cin >> oval[i];
oval[i] %= mod;
}
for(int i = 1; i < n; i++){
int u, v;
cin >> u >> v;
add_edge(u, v);
add_edge(v, u);
}
cnt = 0;
dfs1(rt, 0);
dfs2(rt, rt);
tree.build();
cnt = 0;
LCA::dfs(rt);
LCA::init_ST();
for(int i = 1; i <= m; i++){
int op, x;
cin >> op >> x;
if(op == 1){
int y, v;
cin >> y >> v;
modify_path(x, y, v);
}
if(op == 2){
int y;
cin >> y;
cout << query_path(x, y) << endl;
}
if(op == 3){
int v;
cin >> v;
modify_subtree(x, v);
}
if(op == 4)
cout << query_subtree(x) << endl;
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号