割点&桥 学习笔记

DFS 树

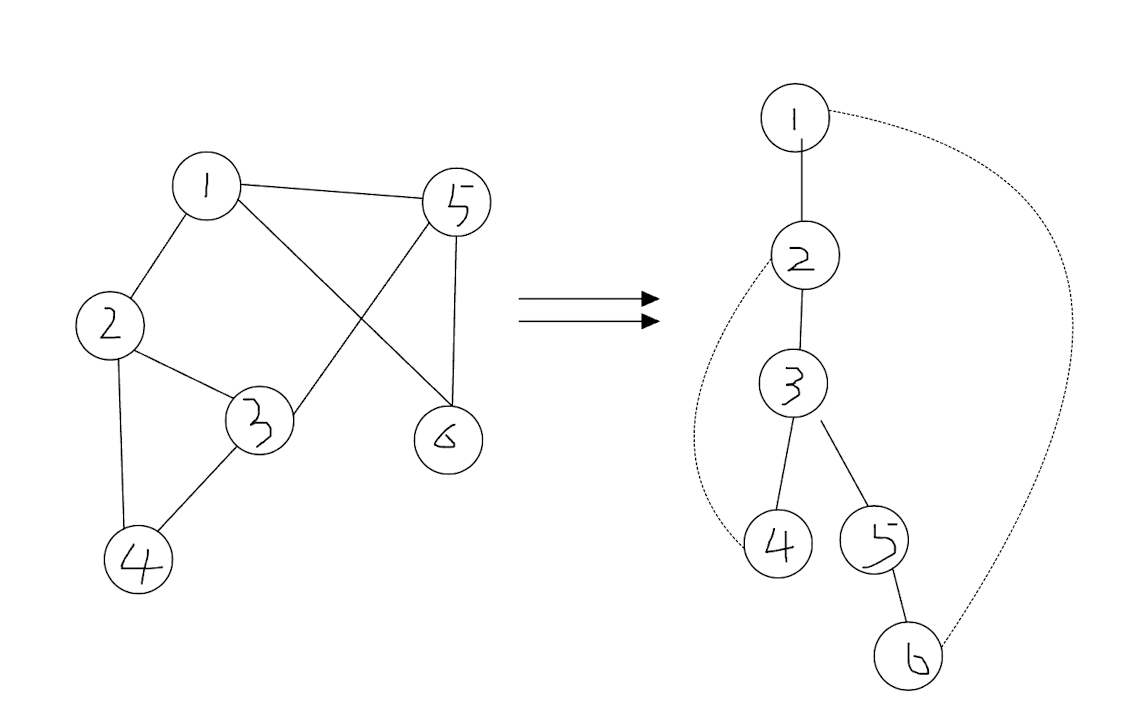
DFS 树是无向图中按照 dfs 的顺序建成的一棵生成树。在 dfs 树上有两种边，树边和回边，顾名思义，树边是生成树上的边而回边是其他边。

下图是一个 dfs 树的例子，树边用实线表示，回边用虚线表示：

割边 || 桥🌉

定义：割边简而言之就是割去这条边后，图会不连通。比如下面的红色边就都是割边：

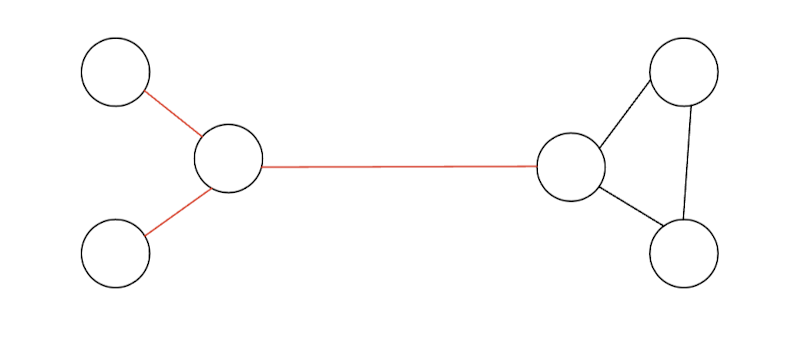
但应该如何求出这样一个边呢？很显然，枚举边并删除后判断连通性显然很难实现，因此 Tarjan 就定义了一个 low 值来解决问题。

low 定义为在 dfs 树上该点能够到达的最低深度，更为具体的，low 值是其子树中所有回边能到的最低深度。

在下图中，蓝色的数字为它的 low 值：

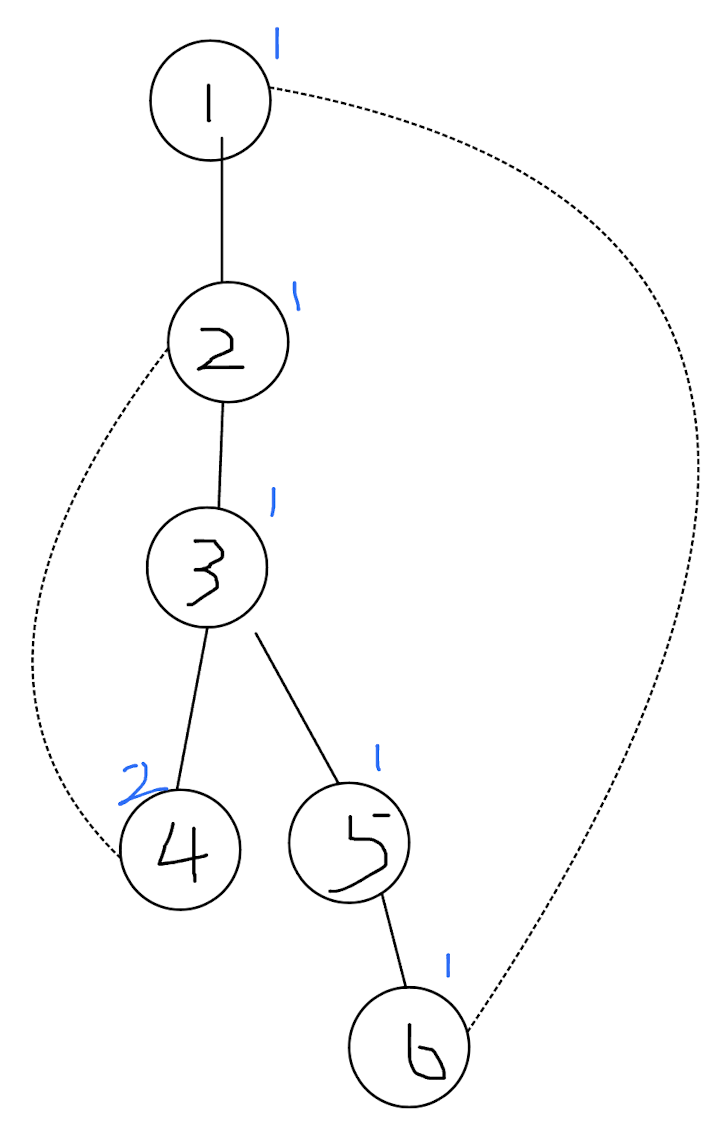
通过观察我们可以发现，一个连接 u，v（v 更深） 的点是割边当且仅当 \(low_v \ge dep_v\) ，因为这条边以下没有任何点可以回到这条边以上的部分。

在实现过程中，运用 dfs 直接模拟 dfs 树，就不用建树了。如果一个点访问过的点已经被访问过了，那就说明是一条回边，更新 \(low_x = dep_v\) 。否则就是树边，继续向下 dfs，回溯时再修改当前点的 low。

代码实现：

//来自洛谷 P1656 炸铁路
#include <iostream>
#include <cstring>
#include <vector>
#include <algorithm>

using namespace std;

typedef struct{
    int to;
    int nxt;
}EDGE;
EDGE edge[10003];
int head[152];
int cnt = 0;
inline void add_edge(int u, int v){
    edge[cnt].to = v;
    edge[cnt].nxt = head[u];
    head[u] = cnt++;
    return;
}
bool vis[152];
int low[152];
int dep[152];
int tot;
vector<pair<int, int> >vec;
inline void tarjan(int u, int fa){
    dep[u] = dep[fa]+1;
    low[u] = dep[u];
    vis[u] = true;
    for(int i = head[u]; ~i; i = edge[i].nxt){
        int v = edge[i].to;
        if(!vis[v]){
            tarjan(v, u);
            low[u] = min(low[u], low[v]);
            if(low[v] > dep[u])
                vec.push_back(make_pair(min(u, v), max(u, v)));
            //如果v无法连到u的祖先节点 切断(u,v)边会产生两个边双连通分量
            //因此(u,v)为桥
        }
        else if(v != fa)
            low[u] = min(low[u], dep[v]);
    }
    return;
}
int main(){
    memset(head, -1, sizeof(head));
    int n, m;
    scanf("%d%d", &n, &m);
    for(int i = 1; i <= m; i++){
        int x, y;
        scanf("%d%d", &x, &y);
        add_edge(x, y);
        add_edge(y, x);
    }
    tarjan(1, 0);
    sort(vec.begin(), vec.end());
    for(auto i : vec)
        printf("%d %d\n", i.first, i.second);
    return 0;
}

割点

割点同割边，也是删去后使图不再连通。

求解方式和求割边相似，但要注意特判根节点，它要有至少两个儿子才能是割点。见代码

//来自洛谷 P3388【模版】割点（割顶）
#include <iostream>
#include <cstdio>
#include <cstring>
#include <vector>
#include <algorithm>

using namespace std;

typedef struct{
    int to;
    int nxt;
}EDGE;
EDGE edge[200002];
int head[20002];
int cnt;
inline void add_edge(int u, int v){
    edge[cnt].to = v;
    edge[cnt].nxt = head[u];
    head[u] = cnt++;
    return;
}
int n;
int dfn[20002];
bool vis[20002];
int dep[20002];
int low[20002];
//dfn[i]:i节点在dfs过程中访问到到顺序
//low[i]:i节点能返回到的最早的节点
int tot;
bool cut[20002];
int root;
inline void tarjan(int u, int fa){
    vis[u] = true;
    dep[u] = dep[fa]+1;
    low[u] = dep[u];
    int sub_tree = 0;
    for(int i = head[u]; ~i; i = edge[i].nxt){
        int v = edge[i].to;
        if(!vis[v]){
            tarjan(v, u);
            sub_tree++;
            low[u] = min(low[u], low[v]);
            //如果儿子能到low[v] 则u也可以到low[v] 更新low[u]
            if(u != root && low[v] >= dep[u])
                cut[u] = true;
            //若子节点不能连到u到祖先节点 则把u去掉后可以分为两个连通分量
            //因此此节点为割点
        }
        else if(v != fa)
            low[u] = min(low[u], dep[v]);
        //如果这个点可以连到比自己早遍历到到点 则需更新low为这个点到dfn
    }
    if(u == root && sub_tree >= 2)
        cut[u] = true;
    //若是一个根 且有两个以上的子树个树
    //则切断此节点后 两个子树会形成两个连通分量
    //因此此节点为割点
    return;
}
inline void print(){//输出
    int ct = 0;
    for(int i = 1; i <= n; i++)
        if(cut[i])
            ct++;
    printf("%d\n", ct);
    for(int i = 1; i <= n; i++)
        if(cut[i])
            printf("%d ", i);
    return;
}
int main(){
    memset(head, -1, sizeof(head));
    int m;
    scanf("%d%d", &n, &m);
    for(int i = 1; i <= m; i++){
        int u, v;
        scanf("%d%d", &u, &v);
        add_edge(u, v);
        add_edge(v, u);
    }
    for(int i = 1; i <= n; i++)
        if(!dfn[i])
            root = i, tarjan(i, 0);
    print();
    return 0;
}