虚树学习笔记

问题引入

在 消耗战 一题中，经常做树形 dp 的小朋友肯定都可以一眼看出这题的朴素算法。

令 \(dp_i\) 为将其子树中（包括自己）的关键点切除所需的最少代价。由此可以列出 dp 式：
当 i 不是关键点的时候，有 $dp_i = \sum_{v\in son(i)}dp_v $。并且所有点的 dp 值都可以等于自己上面最小的边权。

可是这样做明显会超时，怎么优化它呢。通过观察我们不难发现，dp 的状态转移只和关键点有关，因而虚树。虚树可以将关键点单独提出建成一颗新的树，这棵树在结构上与原树相同，但是复杂度可以降低很多，足以通过本题。

虚树 🌲

观察可发现，虚树上的点只可能是关键点或者关键点的 LCA 。但为了方便，一般会把 1 号节点一起放进去。

先将关键点按 dfn 排序，再依次插入树中。在此过程中维护一个最右链，最右链 dfn 递增，且所有在最右链左边的关键点都被处理过。这个链可以用单调栈维护。

插入一个点的时候，如果它在最右链底端点的子树，直接塞入栈中。否则弹栈直到栈顶是其祖先。

特别的，当新点与前最右链中的点的 LCA 还不在树中时，需要同时加入它。

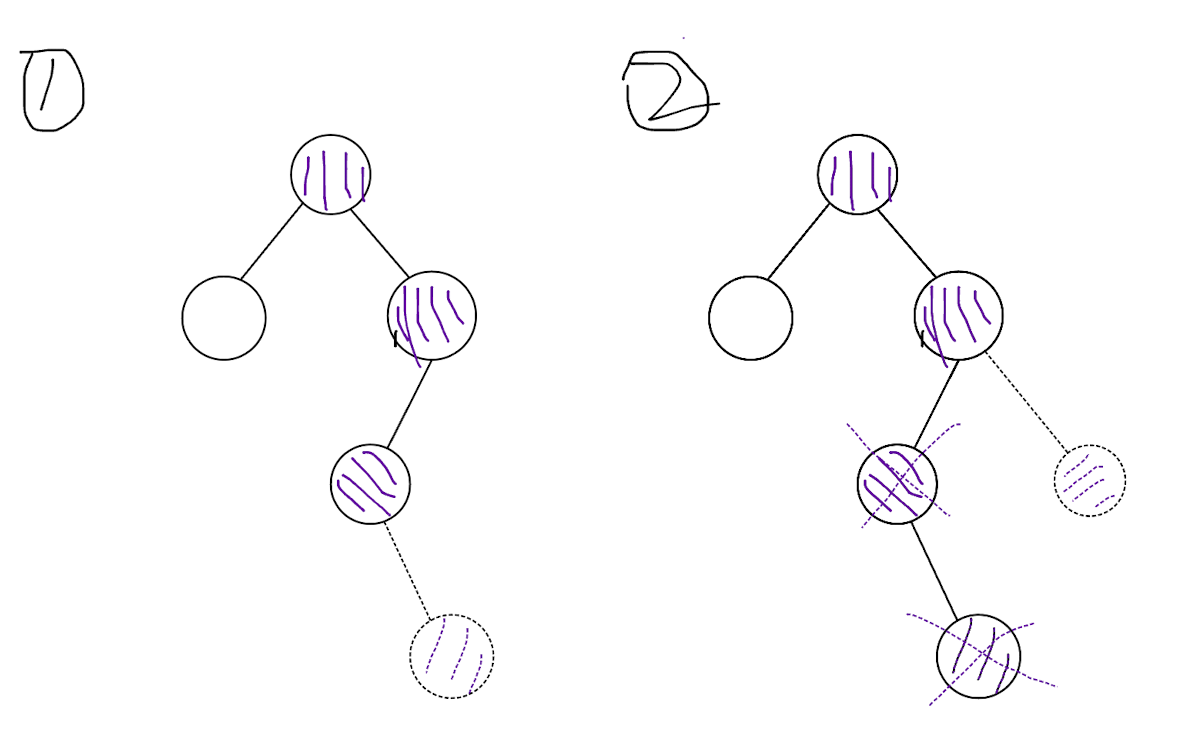
值得注意的是，用完虚数后需还原，要不然会出错。

Code

//
//  虚树.cpp
//  
//  P2495 [SDOI2011] 消耗战
//  Created by HurryCine on 2024/8/3.
//

#include <stdio.h>
#include <iostream>
#include <stack>
#include <cstring>
#include <vector>
#include <algorithm>

using namespace std;

const int N = 5e5;
#define int long long
typedef struct{
    int to;
    int w;
    int nxt;
}Edge;
Edge edge[N<<1];
int head[N];
int cnt;
inline void add_edge(int u, int v, int w){
    edge[cnt].to = v;
    edge[cnt].nxt = head[u];
    edge[cnt].w = w;
    head[u] = cnt++;
}
namespace Graph {   //ST表求LCA
    int tot;
    int eu[N<<1];
    int idx[N];
    int dep[N<<1];
    inline void dfs(int x, int fa){
        eu[++tot] = x;
        idx[x] = tot;
        dep[tot] = dep[idx[fa]]+1;
        for(int i = head[x]; ~i; i = edge[i].nxt)
            if(edge[i].to != fa){
                dfs(edge[i].to, x);
                eu[++tot] = x;
                dep[tot] = dep[idx[x]];
            }
        return;
    }
    int ST[N<<1][30];
    int lg[N<<1];
    inline int get_ans(int x, int y){
        return dep[x] > dep[y] ? y : x;
    }
    inline void init_ST(){
        for(int i = 1; i <= tot; i++){
            lg[i] = lg[i-1];
            if(1<<lg[i-1] == i)
                lg[i]++;
        }
        for(int i = 1; i <= tot; i++)
            ST[i][0] = i;
        for(int i = 1; (1<<i) <= tot; i++){
            for(int l = 1; l+(1<<i)-1 <= tot; l++){
                int r = l+(1<<i)-1;
                int mid = (l+r) >> 1;
                ST[l][i] = get_ans(ST[l][i-1], ST[mid+1][i-1]);
            }
        }
    }
    inline void init_LCA(){
        tot = 0;
        dfs(1, 0);
        init_ST();
    }
    inline int LCA(int x, int y){
        x = idx[x];
        y = idx[y];
        if(x > y)
            swap(x, y);
        int len = lg[y-x+1]-1;
        return eu[get_ans(ST[x][len], ST[y-(1<<len)+1][len])];
    }
};
int dfn[N];
int dep[N];
int minv[N];    //从 1 到 i 路径中的最小边权
inline void dfs(int x, int fa){
    dfn[x] = ++cnt;
    for(int i = head[x]; ~i; i = edge[i].nxt)
        if(edge[i].to != fa){
            dep[edge[i].to] = dep[x] + edge[i].w;
            minv[edge[i].to] = min(minv[x], edge[i].w);
            dfs(edge[i].to, x);
        }
    return;
}
Edge Vedge[N<<1];
int Vhead[N];
bool kee[N];
int cur;
inline bool cmp(int x, int y){
    return dfn[x] < dfn[y];
}
inline void add_Vedge(int u, int v){
    Vedge[cnt].to = v;
    Vedge[cnt].w = 1;
    Vedge[cnt].nxt = Vhead[u];
    Vhead[u] = cnt++;
}
int n;
int dp[N];  //定义 dp[i] 为将 i 的子树切下的最小代价
inline void build_VTree(vector<int>key){
    cnt = 0;
    sort(key.begin(), key.end(), cmp);
    stack<int>sta;  //栈维护右链
    sta.push(1);
    dp[1] = 0;
    for(auto i : key){
        int lca = Graph::LCA(i, sta.top());
        int x;
        while(!sta.empty() && dep[sta.top()] > dep[lca]){
            x = sta.top();
            sta.pop();
            if(dep[sta.top()] >= dep[lca]){
                add_Vedge(x, sta.top());
                add_Vedge(sta.top(), x);
            }
        }
        if(sta.top() != lca){ //如果 lca 不在链上，加入并连边
            sta.push(lca);
            dp[lca] = 0;
            add_Vedge(x, lca);
            add_Vedge(lca, x);
        }
        sta.push(i);
        dp[i] = 0;
    }
    while(sta.size() > 1){
        int x = sta.top();
        sta.pop();
        add_Vedge(x, sta.top());
        add_Vedge(sta.top(), x);
    }
    return;
}

inline void DP(int x, int fa){
    dp[x] = 0;
    for(int i = Vhead[x]; ~i; i = Vedge[i].nxt)
        if(Vedge[i].to != fa){
            DP(Vedge[i].to, x);
            dp[x] += dp[Vedge[i].to];
        }
    if(kee[x])  //关键点可以直接删去
        dp[x] = minv[x];
    else
        dp[x] = min(dp[x], minv[x]);
    Vhead[x] = -1;
    kee[x] = false;
    return;
}
signed main(){
    memset(head, -1, sizeof(head));
    scanf("%lld", &n);
    for(int i = 1; i < n; i++){
        int u, v, w;
        scanf("%lld%lld%lld", &u, &v, &w);
        add_edge(u, v, w);
        add_edge(v, u, w);
    }
    cnt = 0;
    memset(minv, 0x3f, sizeof(minv));
    dfs(1, 0);
    Graph::init_LCA();
    int m;
    cin >> m;
   
    memset(Vhead, -1, sizeof(Vhead));
    while(m--){
        int k;
        scanf("%lld", &k);
        vector<int>v;
        while(k--){
            int x;
            scanf("%lld", &x);
            kee[x] = true;
            v.push_back(x);
        }
        build_VTree(v);
        DP(1, 0);
        printf("%lld\n", dp[1]);
    }
    return 0;
}