题解：CF762D Maximum path

算法

不容易看出，这道题可以用动态规划进行求解。和其他题一样，我们可以设状态 \(dp_{x,y}\) 为到达该点可以得到的最大收益。而本题的数据范围不允许 \(O(n^2)\) 的状态转移，因此每个状态必须从前一两排的状态转移而来。

观察

在读完题后发现，我们题目中的上下左右都可以走其实是迷惑人的。实际上，只有第二排可以向左走……（下图为第三排左转的情况，第一排同理）。

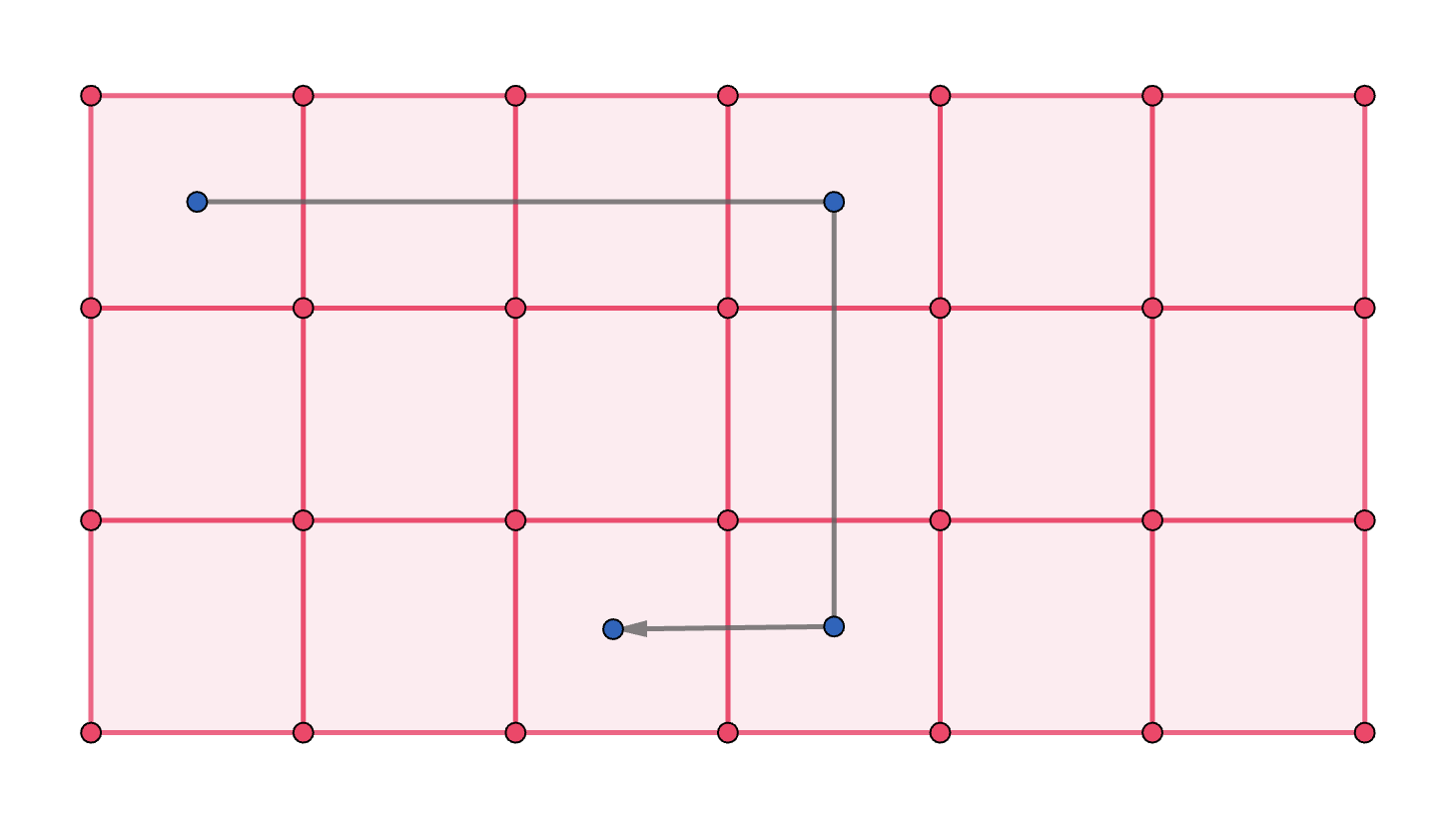
很明显，如果往左移动了，则必定要经过已访问的点，故不成立。

同时我们发现，在第二排向左转后只能做类似蛇形走位的操作。

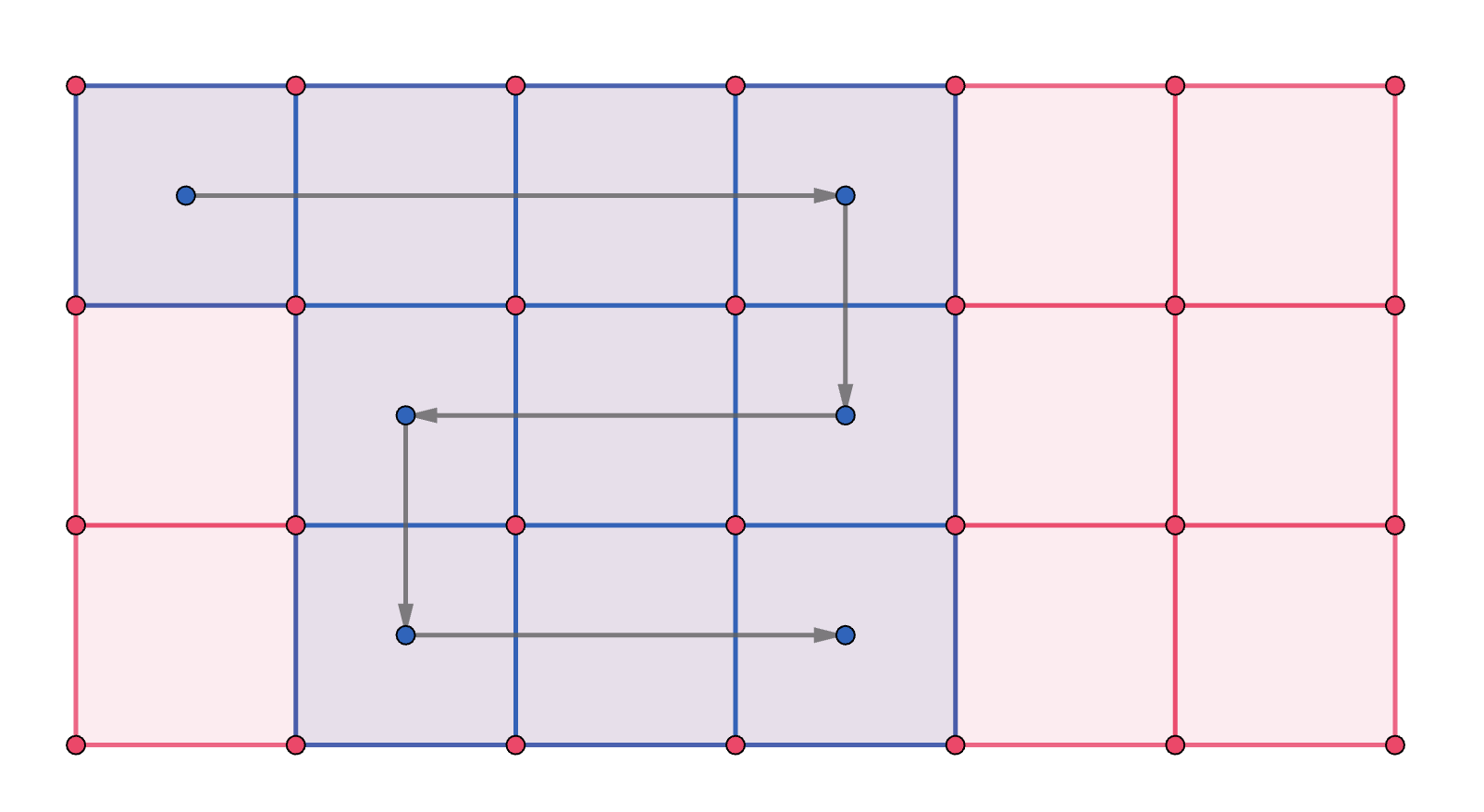
在这种操作后，访问过的点呈一个 \(3\times x\) 的一个矩阵。开始这很明显不可以完成转移，继续观察发现，大的蛇形操作其实可以转化成小的操作来完成。

如果是长为奇数的操作，则可以通过下图方式以达到同样的效果。（因为可以通过简单的上下有移动完成，故无需特别考虑）

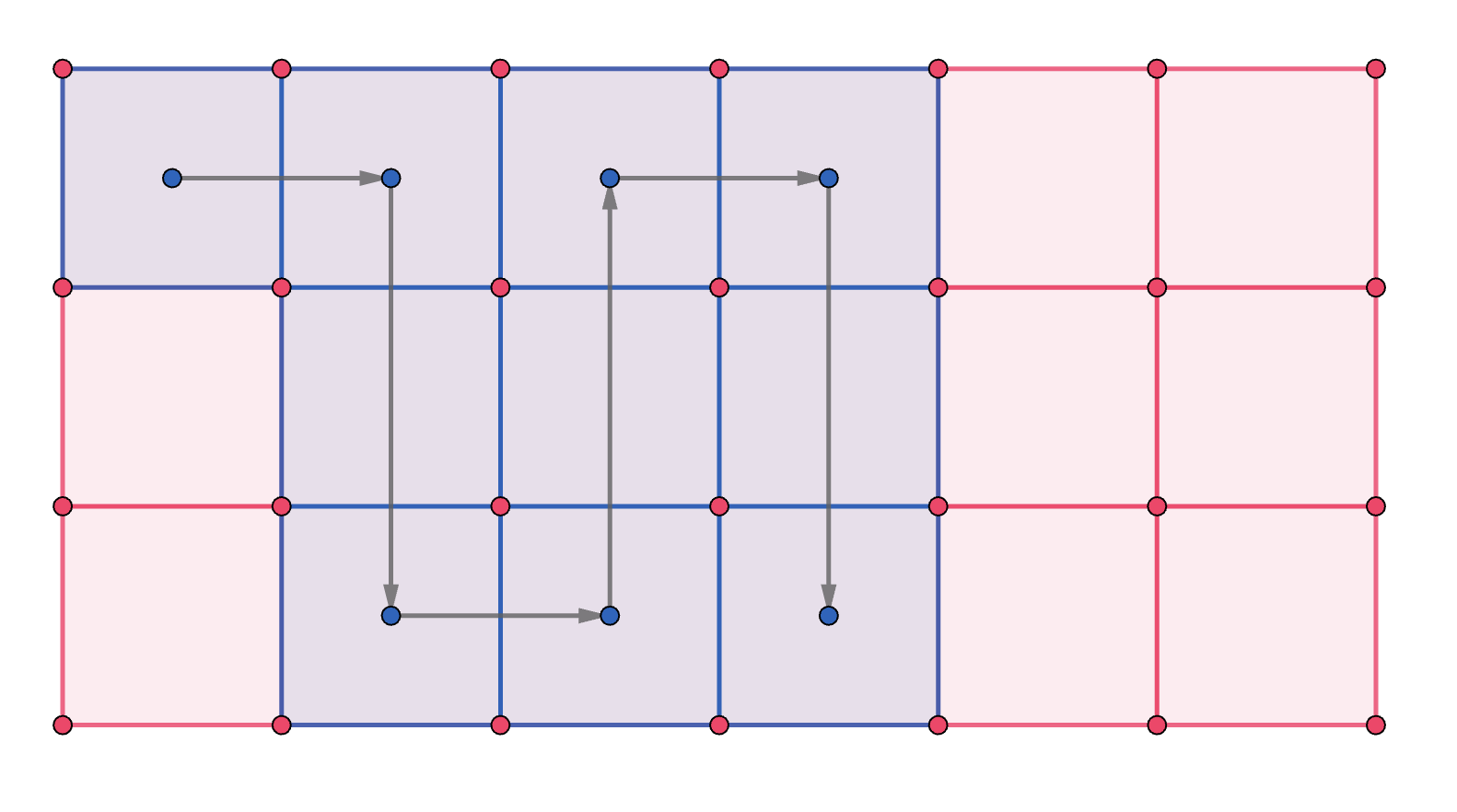
而偶数长度的操作则需要更复杂的转移。（需要特殊考虑）

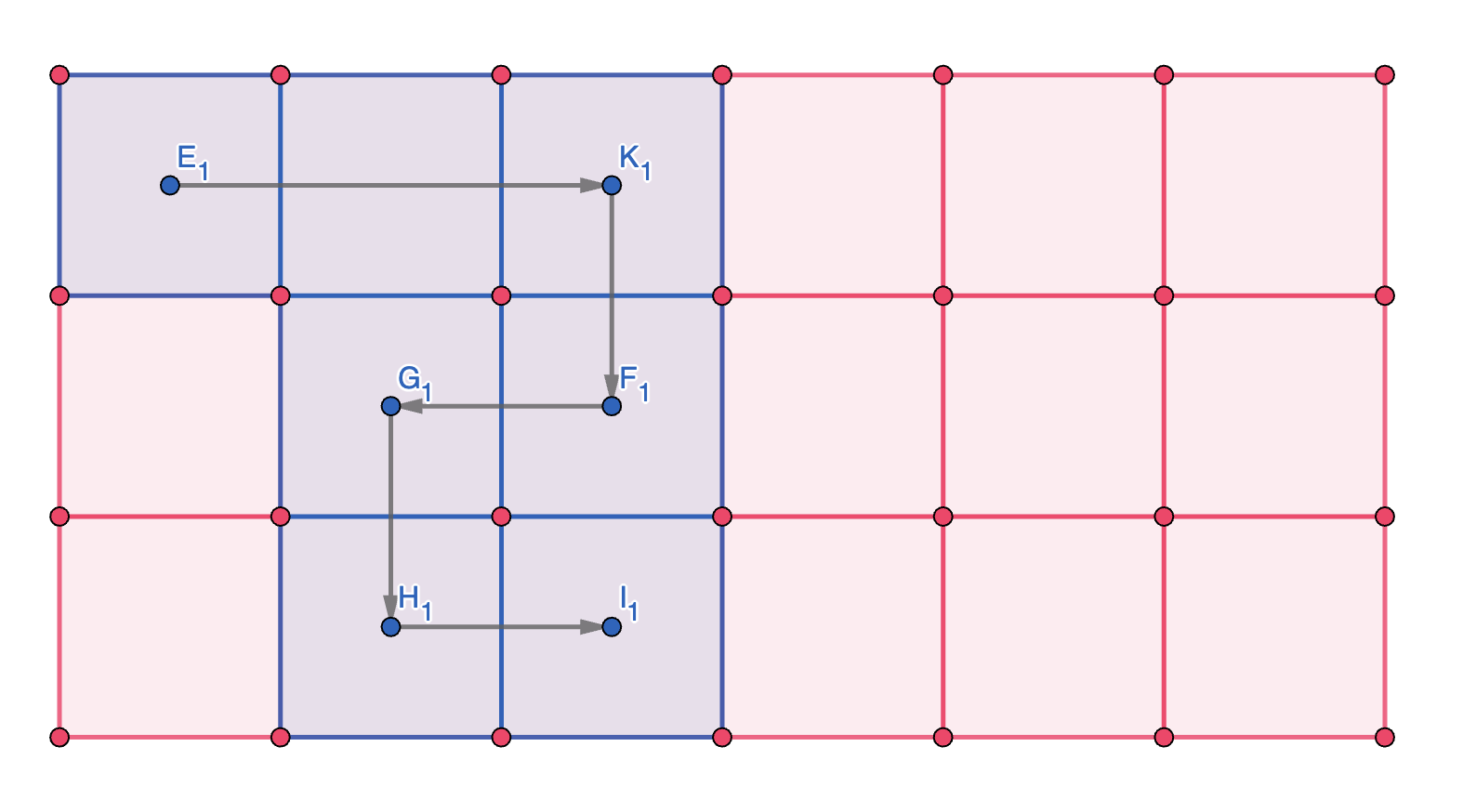
解决完了较为困难的向左走的情况，就可以开始考虑上、下和右的移动了。为了方便转移，我们先向前走一排，再进行上下的移动，这样就可以避免重复走格子了。

状态转移

对于第任意一排，我们都从前一列（或者两列因为有蛇形走位）转移状态。详见下文：

对于第一排，需要考虑蛇形走位，因此状态转移方程为：
\(dp[1][i] = max\begin{cases}dp[1][i-1]+a[1][i]\\dp[2][i-1]+a[2][i]+a[1][i]\\dp[3][i-1]+a[3][i]+a[2][i]+a[1][i]\\dp[3][i-1]+sum[i-1]+sum[i]\end{cases}\)

第二排不用考虑，转移方程：
\(dp[2][i] = max\begin{cases}dp[1][i-1]+a[1][i]+a[2][i]\\dp[2][i-1]+a[2][i]\\dp[3][i-1]+a[3][i]+a[2][i]\end{cases}\)

第三排与第一排类似：
\(dp[3][i] = max\begin{cases}dp[1][i-1]+a[1][i]+a[2][i]+a[3][i]\\dp[2][i-1]+a[2][i]+a[3][i]\\dp[3][i-1]+a[3][i]\\dp[1][i-1]+sum[i-1]+sum[i]\end{cases}\)

Code

点击查看代码

// LUOGU_RID: 168979253
#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

#define int long long
const int N = 1e5+21;
int a[5][N];
int dp[5][N];
int sum[N];
inline int max(int x, int y, int z){
    return x > y ? x > z ? x : z : y > z ? y : z;
}
signed main(){
    int n;
    cin >> n;
    for(int i = 1; i <= 3; i++)
        for(int j = 1; j <= n; j++)
            cin >> a[i][j];
    for(int j = 1; j <= n; j++)
        for(int i = 1; i <= 3; i++)
            sum[j] += a[i][j];	//sum[i] 就是第 i 排的权值和
    memset(dp, -0x3f, sizeof dp);
    dp[1][0] = 0;
    for(int i = 1; i <= n; i++){
        dp[1][i] = max(dp[1][i-1], dp[2][i-1]+a[2][i], dp[3][i-1]+a[2][i]+a[3][i])+a[1][i];
        dp[2][i] = max(dp[1][i-1]+a[1][i], dp[2][i-1], dp[3][i-1]+a[3][i])+a[2][i];
        dp[3][i] = max(dp[1][i-1]+a[1][i]+a[2][i], dp[2][i-1]+a[2][i], dp[3][i-1])+a[3][i];
        //蛇形走位
        dp[1][i] = max(dp[1][i], dp[3][i-2]+sum[i]+sum[i-1]);
        dp[3][i] = max(dp[3][i], dp[1][i-2]+sum[i]+sum[i-1]);
    }
    cout << dp[3][n] << endl;
    return 0;
}