Treap学习笔记
初步认识 Intro
Treap(树堆)是一种 弱平衡 的 二叉搜索树。它同时符合二叉搜索树和堆的性质,名字也因此为 tree(树)和 heap(堆)的组合。 ————OIWiki
\(Treap\)中每个节点设置两个值:\(val\)和\(pri\),分别是值和优先级,在\(Treap\)中,\(pri\)是随机的。在树中,\(val\)是符合二叉搜索树而\(pri\)符合堆性质,这种平衡方式使其能在\(O(logn)\)的时间内完成操作。
\(Treap\)的实现主要依靠旋转,分左旋和右旋两种,他们都可以将根节点向下旋转并且不破坏它的性质。
旋转操作 Zig-Zag
\(Treap\)中的两种基本操作为左旋和右旋,如图所示,左旋将根节点旋转到了左边,将右儿子转到了根部
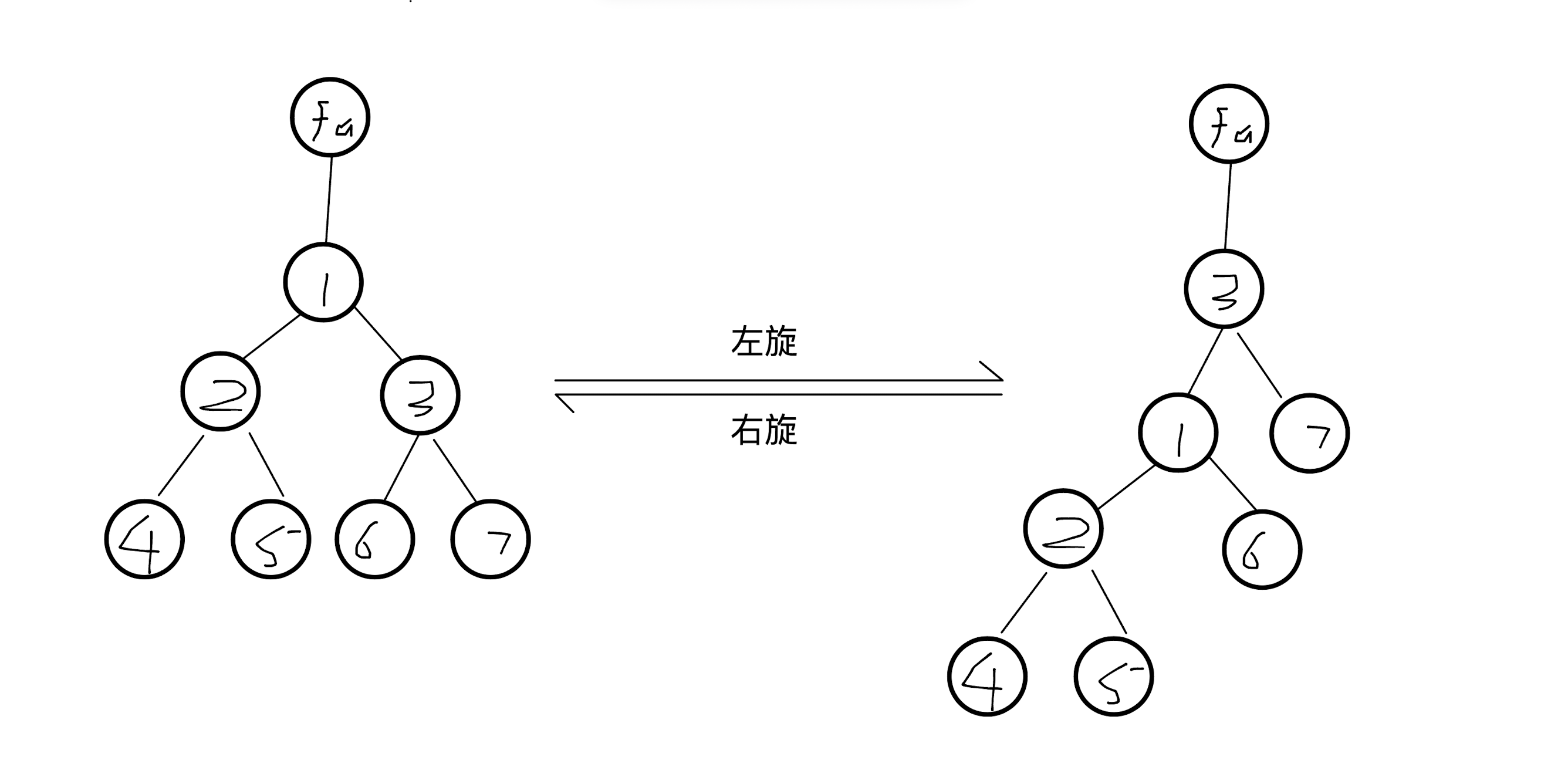
代码实现如下
inline void zig(Node *&cur){ //左旋:把右儿子旋为父亲
Node *tmp = cur->rchild;
cur->rchild = tmp->lchild;
tmp->lchild = cur;
cur->updt(); //更新节点数据
tmp->updt();
cur = tmp;
}
inline void zag(Node *&cur){ //右旋:把左儿子旋为父亲
Node *tmp = cur->lchild;
cur->lchild = tmp->rchild;
tmp->rchild = cur;
cur->updt();
tmp->updt();
cur = tmp;
}
插入 Insert
插入操作基于左旋右旋操作,主要思想为将点插入叶子节点处,再通过旋转将节点移到树中合适的位置。
值得注意的是每个节点会有一个\(cnt\),若在树中找到了一样的点,增加副本数\(cnt\)即可
代码实现:
inline void __insert(Node*&cur, int val){
if(cur == nullptr){
//不存在此节点
//创建新的节点
cur = create(val);
return;
}
if(cur->val == val){
//以前就有这个节点
//加多副本数量即可
cur->cnt++;
cur->size++;
return;
}
//BST
if(cur->val > val){
__insert(cur->lchild, val);
//经过插入 要检查优先级是否有变化
if(cur->rchild != nullptr && cur->rchild->pri < cur->pri)
zag(cur);
}
else{
__insert(cur->rchild, val);
if(cur->lchild != nullptr && cur->lchild->pri < cur->pri)
zig(cur);
}
cur->updt();
return;
}
删除 Delete
删除操作和插入类似,需先找到节点,然后将其旋转到可以直接删除的位置。
在遍历到的节点会有四种情况:
- 当前节点的值不等于想要删除的点,需要继续找
- 当前节点的值为要删掉的点,且它有大于1点副本数,此时直接改变\(cnt\)和\(size\)即可
- 当前节点的值为要删掉的点,且只有一个,此时需要将儿子节点中\(pri\)小的选择上来,将当前节点旋转下去
- 当前节点的值为要删除的点,且只有一个或没有儿子,此时可以直接删除
对于四种情况分别讨论即可
代码实现如下:
inline void __del(Node*&cur, int val){
if(cur->val != val){
//BST
if(cur->val > val)
__del(cur->lchild, val);
else
__del(cur->rchild, val);
cur->updt();
return;
}
if(cur->cnt > 1){
cur->cnt--;
cur->size--;
return;
}
if(cur->lchild == nullptr || cur->rchild == nullptr){
if(cur->lchild == nullptr && cur->rchild == nullptr)
delete cur; //叶子节点可直接删除
//只有一个孩子节点的可以直接删去
//将孩子节点直接接上即可
else if(cur->lchild == nullptr){
Node *tmp = cur;
cur = tmp->rchild;
delete tmp;
}
else{
Node *tmp = cur;
cur = tmp->lchild;
delete tmp;
}
return;
}
//将优先级低的转上去作为根
//此时要删除的节点就被转到这个点的另一侧
//于是递归继续删除
//直到转到可以直接删除的位置
if(cur->lchild->pri < cur->rchild->pri){
zag(cur);
__del(cur->rchild, val);
}
else{
zig(cur);
__del(cur->lchild, val);
}
cur->updt();
return;
}
完整代码:
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
typedef struct Node{
Node *lchild;
Node *rchild;
int val;
int pri;
int cnt;
int size;
inline void updt(){
size = cnt;
if(lchild != nullptr)
size += lchild->size;
if(rchild != nullptr)
size += rchild->size;
return;
}
}Node;
inline Node* create(int val){
Node *newNode = new Node;
newNode->val = val;
newNode->cnt = newNode->size = 1;
newNode->pri = rand();
return newNode;
}
class Treap{
private:
Node *root;
inline void zig(Node*&cur){ //左旋:把右儿子旋为父亲
Node *tmp = cur->rchild;
cur->rchild = tmp->lchild;
tmp->lchild = cur;
cur->updt();
tmp->updt();
cur = tmp;
}
inline void zag(Node*&cur){ //右旋:把左儿子旋为父亲
Node *tmp = cur->lchild;
cur->lchild = tmp->rchild;
tmp->rchild = cur;
cur->updt();
tmp->updt();
cur = tmp;
}
inline void __insert(Node*&cur, int val){
if(cur == nullptr){
//不存在此节点
//创建新的节点
cur = create(val);
return;
}
if(cur->val == val){
//以前就有这个节点
//加多副本数量即可
cur->cnt++;
cur->size++;
return;
}
//BST
if(cur->val > val){
__insert(cur->lchild, val);
//经过插入 要检查优先级是否有变化
if(cur->rchild != nullptr && cur->rchild->pri < cur->pri)
zag(cur);
}
else{
__insert(cur->rchild, val);
if(cur->lchild != nullptr && cur->lchild->pri < cur->pri)
zig(cur);
}
cur->updt();
return;
}
inline void __del(Node*&cur, int val){
if(cur->val != val){
//BST
if(cur->val > val)
__del(cur->lchild, val);
else
__del(cur->rchild, val);
cur->updt();
return;
}
if(cur->cnt > 1){
cur->cnt--;
cur->size--;
return;
}
if(cur->lchild == nullptr || cur->rchild == nullptr){
if(cur->lchild == nullptr && cur->rchild == nullptr)
delete cur; //叶子节点可直接删除
//只有一个孩子节点的可以直接删去
//将孩子节点直接接上即可
else if(cur->lchild == nullptr){
Node *tmp = cur;
cur = tmp->rchild;
delete tmp;
}
else{
Node *tmp = cur;
cur = tmp->lchild;
delete tmp;
}
return;
}
//将优先级低的转上去作为根
//此时要删除的节点就被转到这个点的另一侧
//于是递归继续删除
//直到转到可以直接删除的位置
if(cur->lchild->pri < cur->rchild->pri){
zag(cur);
__del(cur->rchild, val);
}
else{
zig(cur);
__del(cur->lchild, val);
}
cur->updt();
return;
}
inline void __traverse(Node *cur){ //遍历序列,检查
if(cur == nullptr)
return;
__traverse(cur->lchild);
for(int i = 1; i <= cur->cnt; i++)
cout << cur->val << " ";
__traverse(cur->rchild);
return;
}
public:
inline int size(){
return root->size;
}
inline void insert(int val){
__insert(root, val);
}
inline void del(int val){
__del(root, val);
}
inline void traverse(){
__traverse(root);
cout << endl;
}
};
Treap T;
int main(){
int q;
cin >> q;
while(q--){
int op, x;
cin >> op >> x;
if(op == 1)
T.insert(x);
else if(op == 2)
T.del(x);
cout << T.size() << endl;
T.traverse();
}
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号