线段树分治学习笔记

模板题传送门～

目录

• 线段树分治
• 代码实现

线段树分治

线段树分治是一种离线算法，它对时间轴构造了线段树，以处理时间段的处理
举个简单的例子，维护时间[1,4]：

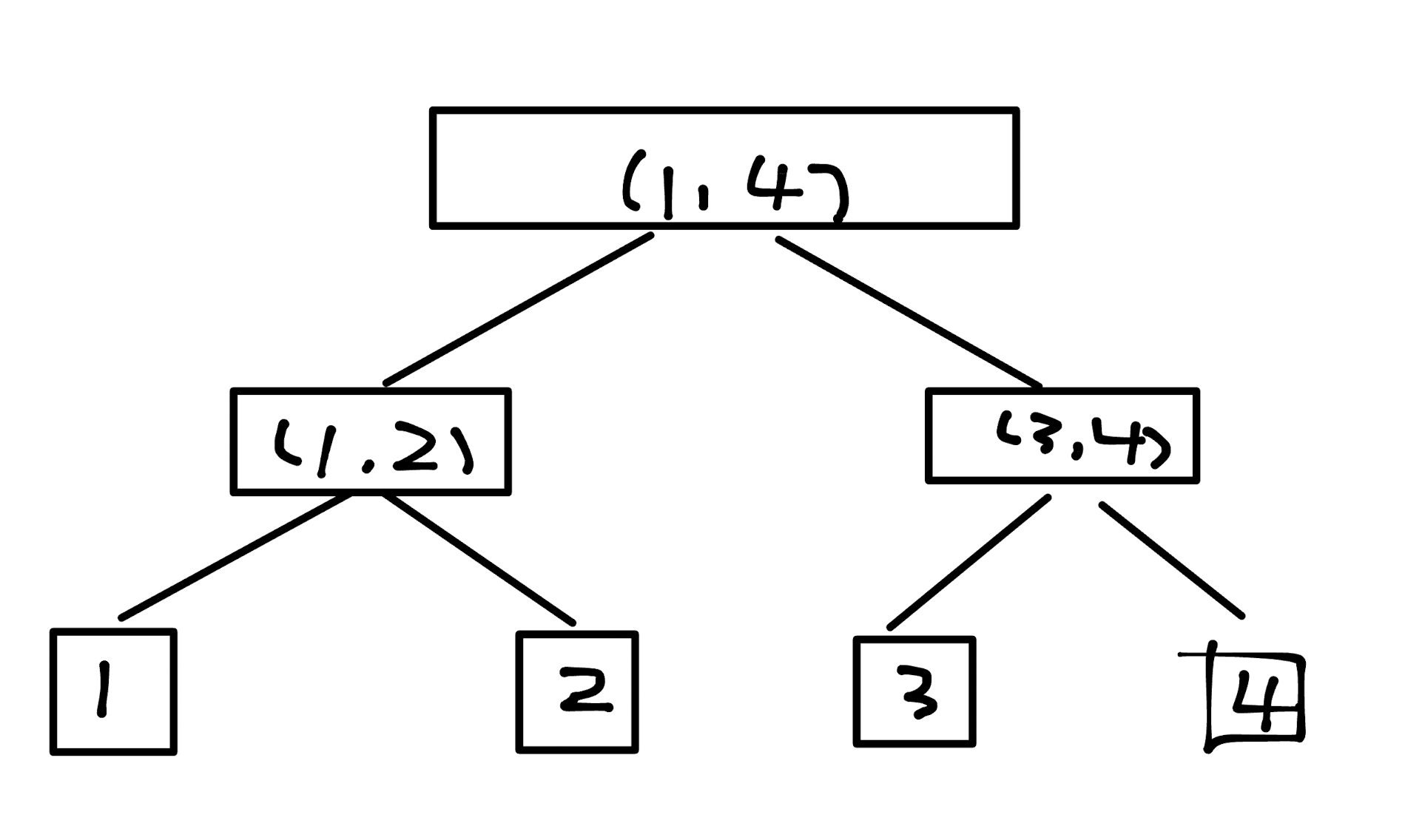
若某次修改从1延伸到3才结束，那么需要修改的便是[1,2]和[3,3]

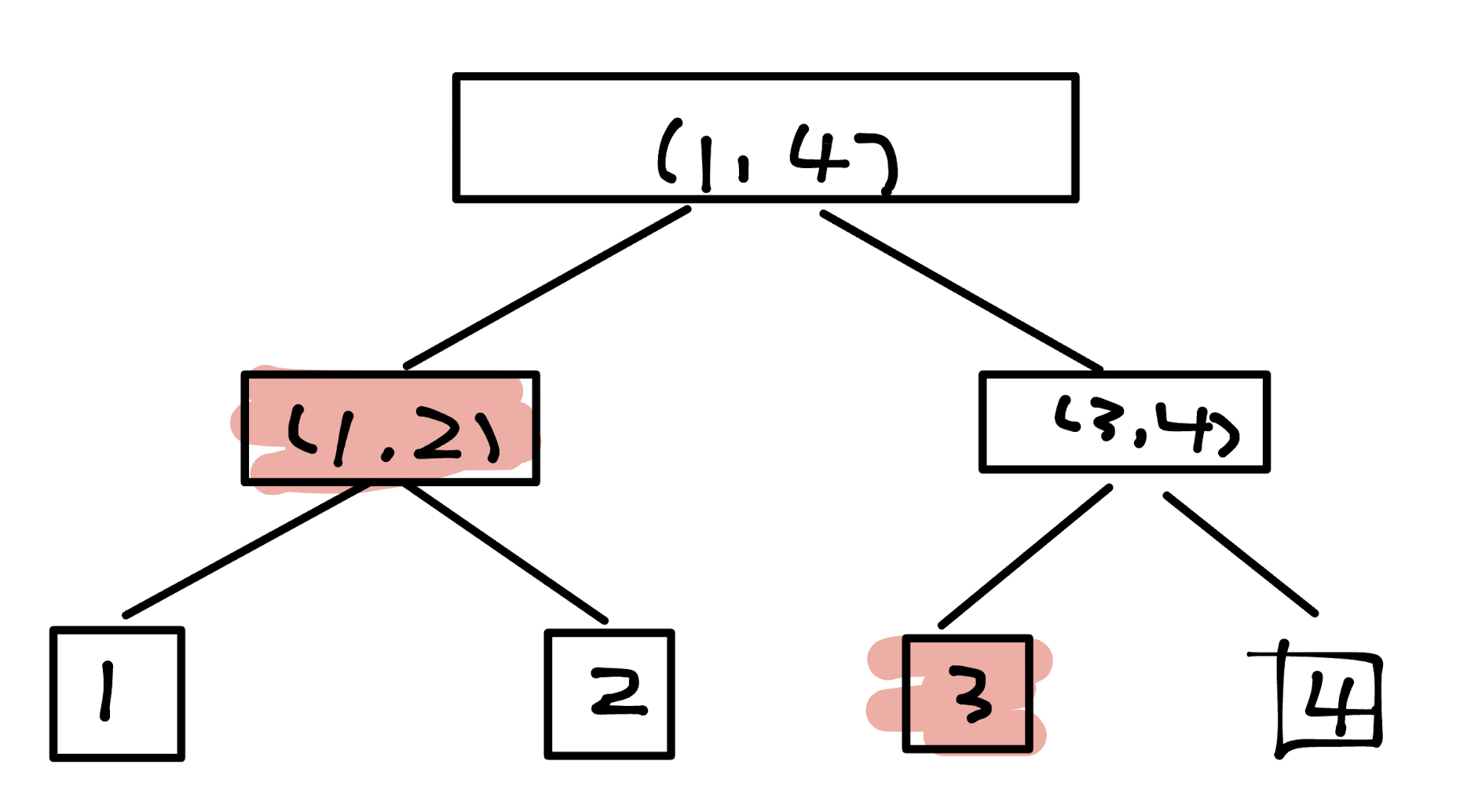
我们给每个节点分配一个vector来存储发生在这个时间段的所有操作。
最后对线段树做深度优先搜索，每次进入一个节点就完成这个节点上的操作，回到这个节点时又把这些操作撤销。
此处运用可撤销并查集维护连通性。

代码实现

//来自loj121 「离线可过」动态图连通性
#include <iostream>
#include <cstring>
#include <stack>
#include <vector>
#include <algorithm>

using namespace std;

const int N = 5e3+7;
const int M = 5e5+8;
#define PII pair<int, int>
typedef struct{	//操作
	int x, y, opt;
}Opt;
Opt a[M];
class DSU{		//可撤销并查集
private:
	int fa[N];
	int dep[N];
	stack<PII>sta;
public:
	inline int size(){
		return sta.size();
	}
	inline void init(int n){
		while(!sta.empty())
			sta.pop();
		for(int i = 1; i <= n; i++)
			fa[i] = i, dep[i] = 0;
	}
	inline int find(int x){	
		if(x == fa[x])
			return x;
		return find(fa[x]);
	}
	inline void join(int x, int y){	//秩合并
		x = find(x);
		y = find(y);
		if(x == y)
			return;
		if(dep[x] > dep[y])
			swap(x, y);
		if(dep[x] == dep[y])
			dep[y]++;
		sta.push(make_pair(x, y));
		fa[x] = y;
	}
	inline bool check(int x, int y){
		return find(x) == find(y);
	}
	inline void undo(int now){	//撤销至第now次操作
		while(sta.size() > now){
			int x = sta.top().first;
			int y = sta.top().second;
			if(dep[y] == dep[x]+1)
				dep[y]--;
			sta.pop();
			fa[x] = x;
		}
		return;
	}
};
bool ans[M];
DSU UN;
vector<Opt>tree[M*5];
inline int lchild(int x){return x<<1;}
inline int rchild(int x){return x<<1|1;}
inline void modify(int p, int pl, int pr, int l, int r, int x){
	if(l <= pl && r >= pr){
		tree[p].push_back(a[x]);
		return;
	}
	int mid = (pl+pr) >> 1;
	if(mid >= l)
		modify(lchild(p), pl, mid, l, r, x);
	if(mid < r)
		modify(rchild(p), mid+1, pr, l, r, x);
	return;
}
inline void dfs(int p, int pl, int pr){
	int tmp = UN.size();
	for(auto i : tree[p])
		UN.join(i.x, i.y);
	if(pl == pr){
		if(a[pl].opt == 2)	//离线记录答案
			ans[pl] = UN.check(a[pl].x, a[pr].y);
		return;
	}
	int mid = (pl+pr) >> 1;
	dfs(lchild(p), pl, mid);
	dfs(rchild(p), mid+1, pr);
	UN.undo(tmp);
}
int n, m;
int st[N][N];
int main(){
	scanf("%d%d", &n, &m);
	UN.init(n);
	for(int i = 1; i <= m; i++){
		scanf("%d%d%d", &a[i].opt, &a[i].x, &a[i].y);
		if(a[i].x > a[i].y)
			swap(a[i].x, a[i].y);
		if(!a[i].opt && !st[a[i].x][a[i].y])
			st[a[i].x][a[i].y] = st[a[i].y][a[i].x] = i;
		else if(a[i].opt == 1)
			modify(1, 1, m, st[a[i].x][a[i].y], i-1, i), st[a[i].x][a[i].y] = st[a[i].y][a[i].x] = 0;
	}
	//没有终点的->在m结束
	for(int i = 1; i <= n; i++)
		for(int j = i+1; j <= n; j++)
			if(st[i][j])
				modify(1, 1, m, st[i][j], m, st[i][j]), st[i][j] = st[j][i] = 0;
	dfs(1, 1, m);
	for(int i = 1; i <= m; i++)
		if(a[i].opt == 2)
			puts(ans[i] ? "Y" : "N");
	return 0;
}