插入排序

class Solution:
    def insertion_sort(self,lst):
        for i in range(1, len(lst)):
            for j in range(i, 0, -1):
                if lst[j] < lst[j - 1]:
                    lst[j], lst[j - 1] = lst[j - 1], lst[j]
                else:
                    break


# 示例用法
solve = Solution()
my_list = [8, 3, 1, 5, 2]
solve.insertion_sort(my_list)
print(my_list)

 

插入排序的步骤如下：

1. 假设要对一个包含 n 个元素的列表进行插入排序。
2. 从列表的第二个元素开始，将其视为当前要插入的元素。
3. 将当前元素与已排序部分的元素进行比较，从右向左逐个比较。
4. 如果当前元素小于已排序部分的某个元素，则将该元素向右移动一位，为当前元素腾出插入的位置。
5. 继续向左比较，直到找到当前元素应该插入的位置（比较的元素较小）或者已经到达已排序部分的起始位置。
6. 将当前元素插入到正确的位置。
7. 重复步骤2至步骤6，直到所有元素都被插入到正确的位置。
8. 完成排序。

class Solution:
    def shell_sort(self,lst):
        # 获取长度
        n = len(lst)
        # 确定gap
        gap = n // 2
        # 当间隔大于0的时候
        while gap > 0:
            # gap开始，步长为n
            for i in range(gap, n):
                # 存储第i个值
                temp = lst[i]
                # i的位置赋予j
                j = i
                # j是i,也就是i大于间隙并且与第i个值相差gap的值大于第i个值
                while j >= gap and lst[j - gap] > temp:
                    # ======下面是相差gap的元素的位置交换===
                    # 直接把与i相差gap的元素赋予给i
                    lst[j] = lst[j - gap]
                    # j值变为i相差gap的位置
                    j -= gap
                # 再将i对应的值赋予给j的位置
                lst[j] = temp
            # 间距缩短一半
            gap //= 2
        # 最终返回排序后的列表
        return lst

# 示例用法
solve = Solution()
my_list = [7,6,9,3,1,5,2,4]
sorted_list = solve.shell_sort(my_list)
print(sorted_list)

希尔排序步骤:

        1.间隔分组

　　 2.组内排序

　　 3.重新设置间隔分组

　　 4.插入排序

 而代码中不是固定分组排序，而是交叉顺序对每组进行排序

 

class Solution:
    # 递归二分,传入数组arr
    def merge_sort(self,arr):
        # 如果长度小于等于1停止(递归停止条件)
        if len(arr) <= 1:
            return arr
        # 取数组的中间位置
        mid = len(arr) // 2
        # 划分为左右两部分
        left_half = arr[:mid]
        right_half = arr[mid:]
        # 划分的部分重复上面的规则继续划分
        left_half = self.merge_sort(left_half)
        right_half = self.merge_sort(right_half)
        # 划分完成后开始对其进行合并
        return self.merge(left_half, right_half)

    # 合并方法
    def merge(self,left, right):
        # 合并最终结果列表
        merged = []
        # 左右索引值
        left_index = 0
        right_index = 0
        # 左部分的索引和右部分的索引必须小于其长
        # =======左右两个数组从头比较大小，小值放到merged中
        while left_index < len(left) and right_index < len(right):
            # 左侧值小于右侧的值
            if left[left_index] < right[right_index]:
                # 先将小的添加到合并结果列表
                merged.append(left[left_index])
                # 左侧索引向下一个移动
                left_index += 1
            else:
                # 先将小的合并再结果列表
                merged.append(right[right_index])
                # 右侧索引+1
                right_index += 1
        # =========两个数组比较之后有个数组为空后，将剩下的数组添加到结果列表
        # 如果左侧部分还有值
        while left_index < len(left):
            # 剩下的值放到结果列表
            merged.append(left[left_index])
            # 并且对应索引+1
            left_index += 1
        # 如果右侧部分还有值
        while right_index < len(right):
            # 右侧的值添加到结果列表中
            merged.append(right[right_index])
            # 并且索引值+1
            right_index += 1
        # 最后返回合并后的列表
        return merged

solve = Solution()
arr = [4, 2, 7, 1, 5, 3, 6]
sorted_arr = solve.merge_sort(arr)
print(sorted_arr)

 

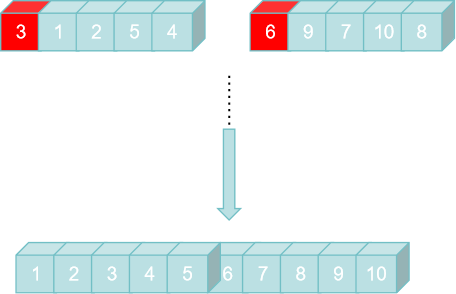
归并排序（Merge Sort）是一种经典的排序算法，它的步骤如下：

1. 将待排序的列表不断地二分，直到每个子列表只包含一个元素（递归的过程）。
2. 对每个子列表进行合并操作，将相邻的两个子列表合并成一个有序的列表。
3. 重复步骤2，直到所有的子列表都被合并成一个有序的列表。

合并操作的步骤如下：

1. 创建一个临时的辅助列表，用于存储合并结果。
2. 从两个已经有序的子列表的开头开始比较它们的元素。
3. 将较小的元素复制到临时列表中，并将对应子列表的指针向后移动一位。
4. 重复步骤3，直到其中一个子列表的元素都被复制到临时列表中。
5. 将剩余的子列表中的元素复制到临时列表的末尾。
6. 将临时列表中的元素复制回原始列表的对应位置。

通过递归地分割和合并操作，归并排序将列表分成越来越小的子列表，直到子列表只包含一个元素。然后通过合并操作将子列表逐步合并成一个有序的列表，直到最终得到完全有序的列表。

 

 

class Solution:
    def quick_sort(self,arr):
        # 数组长度小于等于1,返回当前数组
        if len(arr) <= 1:
            return arr
        # 选择基准元素，基准元素随便选择
        pivot = arr[0]
        # 数组根据基准拆分成左右中三部分
        left = [x for x in arr if x < pivot]  # 小于基准的元素
        middle = [x for x in arr if x == pivot]  # 等于基准的元素
        right = [x for x in arr if x > pivot]  # 大于基准的元素
        # 部分为拆分，整体为合并操作
        return self.quick_sort(left) + middle + self.quick_sort(right)

# 示例用法
solve = Solution()
arr = [3,1,2,5,4]
sorted_arr =solve.quick_sort(arr)
print(sorted_arr)

或者

class Solution:
    def quick_sort(self,arr, low, high):
        if low < high:
            # 分区操作，返回分界点的索引
            pivot_index = self.partition(arr, low, high)

            # 对左侧子列表进行快速排序
            self.quick_sort(arr, low, pivot_index - 1)

            # 对右侧子列表进行快速排序
            self.quick_sort(arr, pivot_index + 1, high)

    def partition(self,arr, low, high):
        # 选择基准元素
        pivot = arr[high]

        # 初始化分界点索引
        i = low - 1

        for j in range(low, high):
            if arr[j] <= pivot:
                # 将小于等于基准元素的元素交换到左侧
                i += 1
                arr[i], arr[j] = arr[j], arr[i]

        # 将基准元素交换到正确的位置
        arr[i + 1], arr[high] = arr[high], arr[i + 1]

        # 返回分界点的索引
        return i + 1

# 示例用法
solve = Solution()
arr = [4, 2, 7, 1, 5, 3, 6]
solve.quick_sort(arr, 0, len(arr) - 1)
print(arr)

 

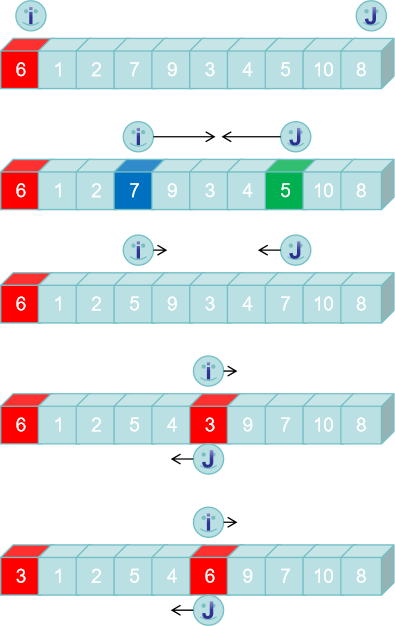
快速排序（Quick Sort）是一种常用的排序算法，其步骤如下：

1. 选择一个基准元素（pivot）。
2. 将列表分割为两个子列表：一个子列表中的元素小于等于基准元素，另一个子列表中的元素大于基准元素。这个过程称为分区（partition）。
3. 对两个子列表递归地应用快速排序算法，重复步骤1和步骤2，直到子列表的长度为1或0，即它们已经有序。
4. 将所有子列表的结果合并成一个有序的列表。

分区的步骤如下：

1. 选取基准元素（可以是列表的第一个元素、最后一个元素、中间元素或随机元素）。
2. 使用两个指针，一个指向列表的起始位置，一个指向列表的末尾位置。
3. 移动起始指针，直到找到一个大于基准元素的元素。
4. 移动末尾指针，直到找到一个小于基准元素的元素。
5. 交换起始指针和末尾指针所指向的元素。
6. 重复步骤3到步骤5，直到起始指针和末尾指针相遇。
7. 将基准元素与相遇位置的元素交换。
8. 返回相遇位置作为分区的分界点。

通过递归地分区和排序操作，快速排序可以将列表分割成越来越小的子列表，并最终得到一个完全有序的列表。