寒假集训Day7
图
今天开始了图论,讲了一些基础内容
首先是存图
存图
这里讲的跟当时高中讲的有些区别,高中当时说了一个链式前向星存图现在没讲,不过没关系,反正讲了也不会,先把今天讲的说了
一个是非常简单的邻接矩阵存图
一个是利用二维vector,每一个vector的行首存初始点,然后一点一点把去向的点往里push,其实这个高中的时候讲过,但是高中的时候感觉有点高深,再加上有链式前向星
就一直不怎么理解,但是链式前向星一直是不会的,就是照着板子写,反而大学之后这个理解一些了
#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
const int N = 100;
struct Edge{
int to,value;
}e;
vector<Edge> G[N+1];
int m,n,tmp;
int main(){
cin>>n>>m;
for (int i=0;i<m;i++){
cin>>tmp>>e.to>>e.value;
G[tmp].push_back(e);
}
for (int i=1;i<=n;i++){
for (int j=0;j<G[i].size();j++){
e=G[i][j];
cout<<"From "<<i<<" to "<<e.to<<", the cost is "<<e.value<<endl;
}
}
return 0;
}
需要存边权的话是这么写的,如果不需要存边权的话
#include <bits/stdc++.h>
using namespace std;
int n,m;
vector <int> t[10001];
int main () {
scanf("%d %d" ,&n,&m);
for(int i = 1;i <= m; i++) {
int u,v;
scanf("%d %d" ,&u,&v);
t[u].push_back(v);
t[v].push_back(u);
}
for(int i = 1;i <= n; i++) {
printf("%d " ,t[i].size());
for(int j = 0;j < t[i].size(); j++) {
tem[j] = t[i][j];
}
sort(tem,tem + t[i].size());
for(int k = 0;k < t[i].size(); k++) {
printf("%d " ,tem[k]);
tem[k] = 0;
}
printf("\n");
}
return 0;
}
这么写就可以了,存无向图的时候正着存一下反着存一下,意味两边都可以互相走就行
dfs
这里主要就是想记录一下在vector存图的情况下用dfs遍历图怎么遍历
我们需要一个judge数组来帮助我们判断当前的点走没走过
然后在dfs函数中,对于我们现在遇到的每一个点,首先,我们要判断这个点接下来还有没有路可以走
如果有的话,我们遍历所有的路,对于我们遇到的每一条路,我们判断他走没走过,如果没走过,我们调用dfs,沿着这条路继续搜下去直到没有路为止
#include <bits/stdc++.h>
using namespace std;
int n,m;
vector<int> a[100001];
bool f[100001];
int ans[100001] = { };
void dfs(int n,int u) {
if(a[u].empty()) return;
for(int i = 0;i < a[u].size(); i++) {
if(f[a[u][i]] == false) {
f[a[u][i]] = true;
ans[n] = max(ans[n],a[u][i]);
dfs(n,a[u][i]);
}
}
}
int main () {
memset(f, false, sizeof(f));
scanf("%d %d" ,&n,&m);
for(int i = 1;i <= n; i++) {
ans[i] = i;
}
for(int i = 1;i <= m; i++) {
int u,v;
scanf("%d %d" ,&u,&v);
a[u].push_back(v);
}
for(int i = 1;i <= n; i++) {
dfs(i,i);
printf("%d " ,ans[i]);
memset(f,false,sizeof(f));
}
return 0;
}
拓扑排序
根据百度百科的定义,拓扑排序是用了来解决这样问题的:对于一个有向无环图,把其顶点转化成一个线性序列,要求这个序列,对于任意一条边而言起点都在终点前面
那么他的过程就是这样的:
首先我们找到一个入度为0的点,输出这个点,然后删掉这个点,继续找下面入度为0的点,重复上述过程,就能得到拓扑排序中要求的线性序列
从CSDN找了个图,具体解释一下拓扑排序的过程:
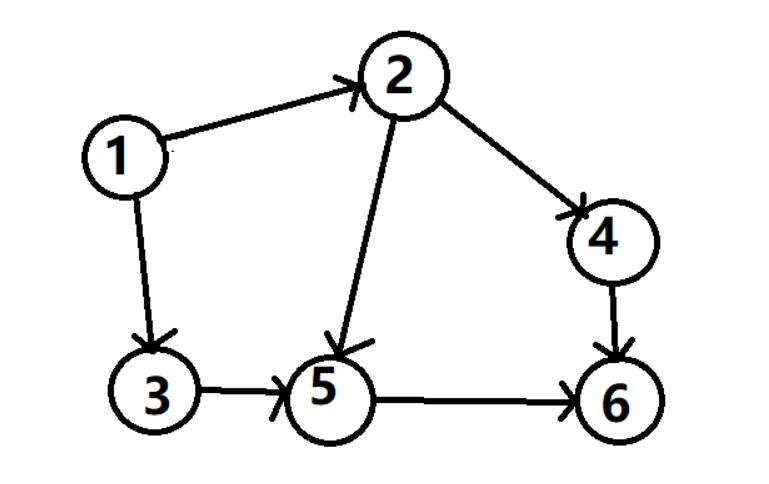
首先找到1,输出1,然后删掉1
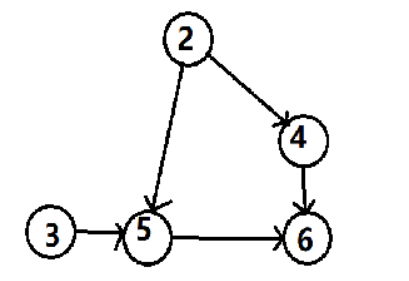
重复上述过程找到2

然后以此类推
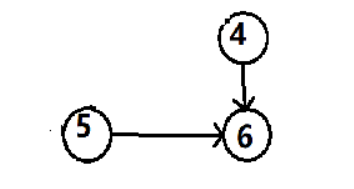
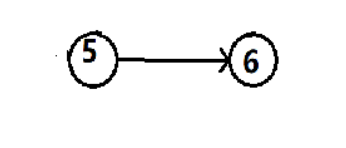

具体的代码实现是这样的:
#include <bits/stdc++.h>
using namespace std;
int n;
vector<int> a[1000001];
queue<int> q;
int in[10000001] = { };
int main () {
scanf("%d" ,&n);
for(int i = 1;i <= n; i++) {
int x;
while(1) {
scanf("%d" ,&x);
if(x == 0) break;
a[i].push_back(x);
in[x]++;
}
}
for(int i = 1;i <= n; i++) {
if(in[i] == 0) {
q.push(i);
}
}
while(!q.empty()) {
int sum = q.front();
printf("%d " ,sum);
q.pop();
for(int i = 0;i < a[sum].size(); i++) {
int now = a[sum][i];
in[now]--;
if(in[now] == 0) {
q.push(now);
}
}
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号