利用BM算法和KMP算法完成给定的字符串查找

一、利用BM算法和KMP算法完成给定的字符串查找

根据KMP算法思想用编程语言实现如下：

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
using namespace std;

/*
char pattern[]:所要查找的字符串 
int prefix[]:pattern字符串对应的前缀表 
int n:pattern字符串长度 
*/
void prefix_table(char pattern[],int prefix[],int n)
{
	int len=0;
	int i=1;
	prefix[0]=0;
	while(i<n)
	{
		if(pattern[i]==pattern[len])
		{
			len++;
			prefix[i]=len;
			i++;
		}
		else
		{
			if(len>0)
			{
				len=prefix[len-1];
			} 
			else
			{
				//此时len为0对应i=1且len=0的情形 
				prefix[i]=len;
				i++;
			}
		}
	}
}
/*
*移动prefix表，为KMP算法做准备,同时对KMP算法进行改进，初始化nextval数组 
*/
void move_prefix_table(int prefix[],int n)
{
	int i;
	for(i=n-1;i>0;i--)
	{
		prefix[i]=prefix[i-1];
	}
	prefix[0]=-1;
	
}
//对目标串和模式串应用KMP算法进行搜索 
void kmp_search(char* text,char* pattern)
{
	//目标串text[i]      len[text]=m
	//要匹配的字符串pattern[j]   len[pattern]=n;
	int i=0,j=0,k;
	int n=strlen(pattern);
	int m=strlen(text);
	int prefix[n];
	int nextval[n];
	//构造前缀表 
	prefix_table(pattern,prefix,n);
	move_prefix_table(prefix,n);
	//初始化nextval数组 
	nextval[0]=-1;
	for(k=1;k<n;k++)
	{
		//当下一个要匹配的字符与当前错配的字符相同时 
		if(pattern[k]==pattern[prefix[k]])
		{
			nextval[k]=nextval[prefix[k]];
		}
		else
		{
			nextval[k]=prefix[k];	
		}
	}
	for(k=0;k<n;k++)
	{
		cout<<nextval[k];
	}
	cout<<endl;
	for(k=0;k<m;k++)
	{
		printf("%3d",k);
	}
	cout<<endl;
	for(k=0;k<m;k++)
	{
		printf("%3c",text[k]);
	}
	cout<<endl;
	//对目标字符串进行遍历 
	while(i<m)
	{
		if(j==n-1&&text[i]==pattern[j])
		{
			printf("Found %s at %d\n",pattern,i-j);
			j=nextval[j];
		}
		if(j>=0&&text[i]==pattern[j])
		{
			i++;
			j++;
		}
		else
		{
			j=nextval[j];
			//当第一个字母匹配不上时，下标同时向右移动 
			if(j<0)
			{
				i++;
				j++;
			}
		}
	}
}

int main()
{
	char pattern[]="ABABCA";
	char text[]="ABABCABABCCBABCABABCA";
	kmp_search(text,pattern);
	return 0;
}

KMP算法的运行结果如下：

根据BM算法思想用编程语言实现如下：

#include <cstdio>
#include <cstring>
#include <iostream>
using namespace std; 

//256个ASCII字符
int ASIZE=256;

//设计一个数组bmBc['k']，表示坏字符‘k’在模式串中出现的位置距离模式串末尾的最大长度，
//那么当遇到坏字符的时候，模式串可以移动距离为： shift(坏字符) = bmBc[T[i]]-（m-1-i)。
void preBmBc(char *x, int m, int bmBc[])
{
	int i;
	for (i = 0; i < ASIZE; ++i)
	{
		bmBc[i] = m;
	}
	for (i = 0; i <= m - 1; ++i)
	{
		bmBc[x[i]] = m - i - 1;
	}
}
//suffix[i] = s 表示以i为边界，与模式串后缀匹配的最大长度，
//如下图所示，用公式可以描述：满足P[i-s, i] == P[m-s, m]的最大长度s。
void suffixes(char *x, int m, int *suff)
{
	suff[m-1]=m;
	for (int i=m-2; i>=0; --i)
	{
		int q=i;
		while(q>=0&&x[q]==x[m-1-i+q])
		{
			--q;
		}
		suff[i]=i-q;
	}
}
//bmGs[i] 表示遇到好后缀时，模式串应该移动的距离，
//其中i表示好后缀前面一个字符的位置（也就是坏字符的位置）
void preBmGs(char *x, int m, int bmGs[])
{
	int i, j, suff[m];
	suffixes(x, m, suff);
	//情景三、模式串中没有子串匹配上好后缀，但找不到一个最大前缀
	for (i = 0; i < m; ++i)
	{
		bmGs[i] = m;
	}
	j = 0;
	//情景二、模式串中没有子串匹配上好后缀，但找到一个最大前缀
	//原因在于如果i,j(i>j)位置同时满足第二种情况，那么m-1-i<m-1-j，
	//而(bmGs[j] == m)保证赋值为m-1-i，这也说明了为什么要从后往前计算。
	for (i = m - 1; i >= 0; --i)
	{
		//suff[i] = s 表示以i为边界，与模式串后缀匹配的最大长度
		//我们知道x[i+1-suff[i]…i]＝＝x[m-1-siff[i]…m-1],而suff[i]==i+1，
		//我们知道x[i+1-suff[i]…i]=x[0,i],也就是前缀，满足第二种情况。
		if (suff[i] == i + 1)
		{
			for (; j < m - 1 - i; ++j)
			{
				if (bmGs[j] == m)
				{
					bmGs[j] = m - 1 - i;
				}
			}
		}
	}
	//情景一、模式串中有子串匹配上好后缀
	//i从小到大原因在于如果suff[i]==suff[j]，i<j，
	//那么m-1-i>m-1-j,我们应该取后者作为bmGs[m - 1 - suff[i]]的值。
	for (i = 0; i <= m - 2; ++i)
	{
		bmGs[m - 1 - suff[i]] = m - 1 - i;
	}
}
void BM(char *x, int m, char *y, int n)
{
	int i, j, bmGs[m], bmBc[ASIZE];
	/* Preprocessing */
	preBmGs(x, m, bmGs);
	preBmBc(x, m, bmBc);
	for(i=0;i<n;i++)
	{
		printf("%3d",i);
	}
	cout<<endl;
	for(i=0;i<n;i++)
	{
		printf("%3c",y[i]);
	}
	cout<<endl;
	/* Searching */
	j = 0;
	while (j <= n - m)
	{
		for (i = m - 1; i >= 0 && x[i] == y[i + j]; --i);
		if (i < 0)
		{
			cout<<"find "<<x<<" at "<<j<<endl;
			j += bmGs[0];
		}
		else
		{
			j += max(bmGs[i], bmBc[y[i + j]] - m + 1 + i);
		}
	}
}

int main()
{
	char text[]="ABXABCCATYABCCABCCABABCC";
	char patten[]="ABCCA";
	int m=strlen(patten);
	int n=strlen(text);
	BM(patten,m,text,n); 
	return 0;
} 

BM算法的运行结果如下：

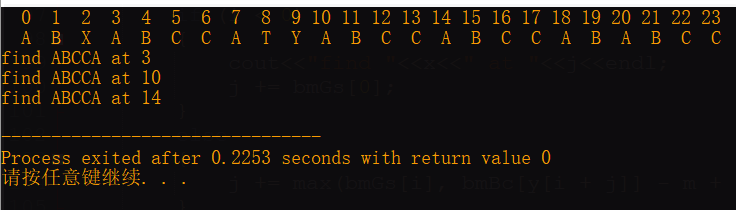
二、总结这两类字符串查找算法的特点、并进行性能比较

​ KMP算法在进行字符串的从前往后匹配时，利用了next数组将之前串匹配的成功经验存储下来，从而加快了字符串的匹配速度。这使得KMP算法的最好性能、平均性能、最差性能的时间复杂度均为O(m+n)。

​ BM算法在进行从右往左的字符串匹配过程中，充分利用了好后缀与坏字符在字符串匹配过程中对于指针移动的影响，应用这两个策略设计而成的BM算法在最好情况下的时间复杂度为O(n/m)、最坏情况下的时间复杂度为O(m+n)。