Errich-Tac-Toe (Hard Version)

题目链接：点击进入

题意

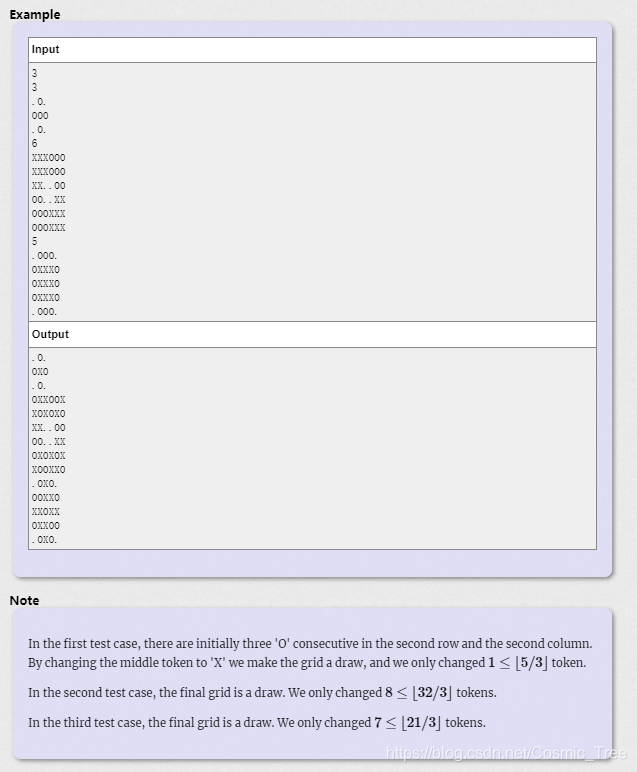
给你一个 n * n 的方格矩阵，每个方格可以标记 X 或者 标记 O 或者 啥也不标记 ，如果有 三个连续的 X 或者 三个连续的 O 形成一行 或者 一列（ 斜着不行，只能与 x轴 或者 y 轴平行 ）说明是一个成功的配置，否则是绘制配置；
给你原矩阵，你最多可以操作 [ k / 3 ] 次（ 向下取整 ，k 是 X 与 O 的总个数 ），每次操作可以把 X 变为 O 或者 把 O 变为 X ，要求你将原矩阵变为绘制配置，同时输出改变后的矩阵（不要求操作数最少）

思路

三个连续的 X 或者 O 是成功配置的标志，我们只要改变三个位置中的其中一个就可以，但是考虑到 “ 连环消消乐 ” 的情况，我们可以采用（ x + y ）% 3（ x 行标 ，y 列标 ），的方式来确定改变哪个位置的标记（ 跟黑白染色差不多的 ，如果三个连续的 X 或者 O 在一列 或者 一行，那么三个的位置 %3 的结果将各不同 ）；
配个官方图（图片来自官方题解）

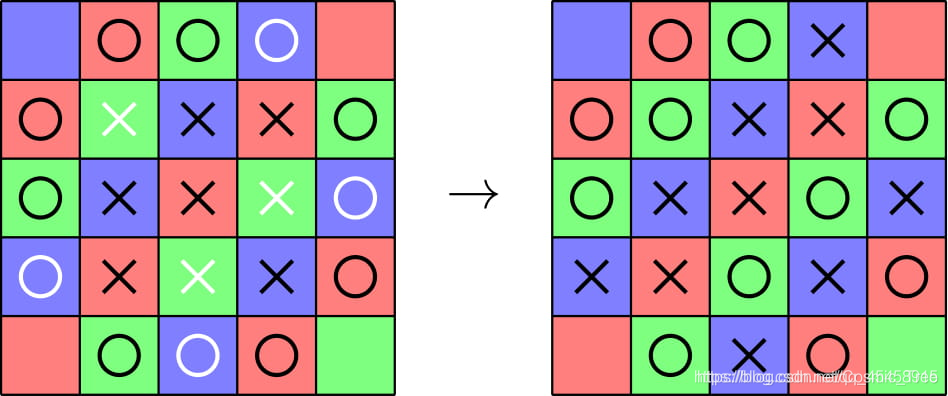
知道这个特点，那我们改变哪个位置的标记呢，当然是改变次数越小越好了，选标记数最少的位置（ 这个位置标记的数目最少 ，操作也最少 ）；

同时考虑到改完 X 可能跟 O 又凑成三个（ 或者改完 O 可能跟 X 又凑成三个 ），我们可以对于 X 和 O ，不改变相同的位置，这样改变后也不会出现连续的了。

代码

#include<cstdio>
#include<algorithm>
#include<cmath>
#include<queue>
#include<iostream>
#include<cstring>
#define inf 0x3f3f3f3f
using namespace std;
typedef long long ll;
const int maxn=1e6+10;
int n,t,cnt[5][5];
char s[310][310];
int main()
{
    ios::sync_with_stdio(false);
    cin>>t;
    while(t--)
    {
    	cin>>n;
    	for(int i=1;i<=n;i++)
    		for(int j=1;j<=n;j++)
    			cin>>s[i][j];
    	for(int i=1;i<=n;i++)
    	{
    		for(int j=1;j<=n;j++)
			{
				if(s[i][j]=='.') continue;
				int pos=(i+j)%3;
				if(s[i][j]=='O') cnt[pos][0]++;
				else cnt[pos][1]++;
			}
		}
		int minn=inf,x,y;
		for(int i=0;i<3;i++)
		{
			for(int j=0;j<3;j++)
			{
				if(i==j) continue;
				if(minn>cnt[i][0]+cnt[j][1])
				{
					minn=cnt[i][0]+cnt[j][1];
					x=i,y=j;
				}
			}
		}
		for(int i=1;i<=n;i++)
		{
			for(int j=1;j<=n;j++)
			{
				if(s[i][j]=='.') continue;
				int pos=(i+j)%3;
				if(s[i][j]=='O'&&pos==x) s[i][j]='X';
				else if(s[i][j]=='X'&&pos==y) s[i][j]='O';
			}
		}
		for(int i=1;i<=n;i++)
		{
			for(int j=1;j<=n;j++)
				cout<<s[i][j];
			cout<<endl;
		}
		for(int i=0;i<3;i++) 
			for(int j=0;j<3;j++)
				cnt[i][j]=0;
	}
    return 0;
}