数学总结 1（Lucas 定理、欧拉定理、阶、原根、指数方程）

零、目录

数论滚出 OI！数论滚出 OI！数论滚出 OI！数论滚出 OI！数论滚出 OI！【魔怔】【魔怔】【魔怔】

1. Lucas 定理
2. ExLucas 定理
3. 欧拉定理
4. 扩展欧拉定理
5. 阶
6. 原根
7. BSGS 算法
8. ExBSGS 算法
9. N 次剩余（Easy Version）
10. N 次剩余（Hard Version）

一、Lucas 定理

若 $p$ 为质数，则有：
$$\binom{n}{m} = \binom{\lfloor \frac{n}{p} \rfloor}{\lfloor \frac{m}{p} \rfloor} \times \binom{n \bmod p}{m \bmod p}$$

特别地，若 $n \gt m$ 则钦定 $\binom{n}{m} = 0$。
也可以理解为 $n,m$ 在 $p$ 进制下每一位分别组合数的乘积。
该算法适用于 $p$ 较小的情况，这样后者可以用阶乘快速计算，前者可以递归求解。

Code.

推论 1

对于任意的 $p$，只要对于每一位 $n_i \geq m_i$，就有 $\binom{n}{m} \not=0$。该推论例题：洛谷 P8688 蓝桥杯 2019 省 A 组合数问题。

特殊地，当 $p=2$，$\binom{n}{m} \bmod 2 = 1 \Longleftrightarrow (n \And m) = m$。
相当于二进制下，每一位 $i$ 都有 $n_i \geq m_i$，因此与运算后结果为 $m$。

不太重要的推推论：杨辉三角每一位 $\bmod 2$ 之后会呈现分形结构。

推论 2

$\binom{a+b}{a} \bmod p \not= 0 \Longleftrightarrow a+b$ 在 $p$ 进制下加法无进位。
Lucas 定理的直接推论。

推论 3

$\binom{a+b}{a}$ 分解质因数后 $p$ 的指数（即出现次数）$=a+b$ 在 $p$ 进制下进位次数。

---

二、ExLucas 定理

Lucas 定理中保证模数 $p$ 是质数，如果不是质数怎么办呢？
处理合数取模的一般思路：

• 将模数分解质因数 $M = p_1^{a_1} p_2^{a_2} \dots p_k ^{a_k}$。
• 分别求出 $(ans_1 \bmod p_1^{a_1}), (ans_2 \bmod p_2^{a_2}), \dots, (ans_k \bmod p_k^{a_k})$。
• 由于各个质数幂之间互质，所以可以用中国剩余定理（CRT）求解。

现在问题转化为如何求 $\binom{n}{m} \bmod p^k$。
即求解 $\frac{n!}{m!(n-m)!} \bmod p^k$。

注意分母可能不可逆，因为它可能不与 $p^k$ 模数互质。
如何把它强转为可逆？

如果我们可以分解阶乘：即 $n! \to X’ \times p^{Y_n}$，再令 $X_n = X’ \bmod p^k$……
那么 $\frac{n!}{m!(n-m)!} = \frac{X_n}{X_m X_{n-m}} \times p^{Y_n - Y_m - Y_{n-m}}$。
这样分母 ${X_m X_{n-m}}$ 就一定与 $p^k$ 互质，可逆了。

$Y_n$ 的计算：

• $Y_n$ = $\lfloor \frac{n}{p} \rfloor + \lfloor \frac{n}{p^2} \rfloor + \dots$
• 即有几个 $p$ 的因子就会被算几次。
• 小推论：$Y_n$ 等价于 $n$ 减去 $n$ 在 $n$ 进制中数位和，再除以 $p-1$。

$X_n$ 的计算：

假设现在要计算 $23! \bmod 9$，其中 $n=23,p=3,k=2$，即 $p^k=9$。
考虑“劲爆”地把它们每 $p$ 个一行分组。

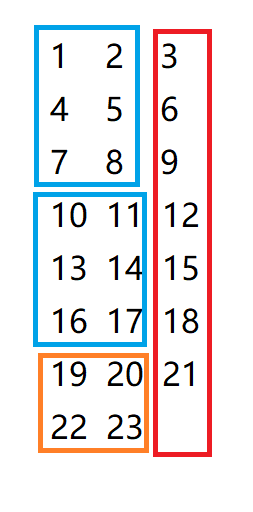
观察到每行的最后一个数一定是 $p$ 的倍数，把它们全部都 $\div p$，它们的乘积就是 $\lfloor \frac{23}{3} \rfloor = 7$ 的阶乘 $7!$。
这是一个子问题，可以递归做，所以把它抛开不管。

问题是怎么计算前面的乘积？
由于每行最后一个已经被叉出去了，所以前面的都与 $p$ 互质。
这时候再把它们每 $p^k$ 个分一组，就会形成若干个“整块”和最后一个“散块”。
考虑预处理 $f_i$ 表示 $[1,i]$ 内所有与 $p$ 互质的数的乘积。
由于 $\bmod p^k$，所以每个块内的阶乘都是一样的。
已经处理完 $f$，所以左边这些的乘积就是 $f(p^k)^{\lfloor \frac{n}{p^k} \rfloor} \times f(n \bmod p^k)$，类似于分块。

因此只需要预处理 $f$ 数组就可以通过递归子问题在 $O(\log_p n)$ 的时间复杂度内求解 $X$ 数组。

Code.

事实上这东西大概率不考。
省选场在一道计数题的基础上套一个合数取模，光是想想就非常逆天了。

---

三、欧拉定理

当 $\gcd(a, m) = 1$ 时，有 $a^{\varphi(m)} \equiv 1 \pmod m$。

应用：

• 对于质数 $p$，有 $a^{p-1} \equiv 1 \pmod p$，因此 $a^{-1} \equiv a^{p-2} \pmod p$，快速幂求逆元。
• 计算 $a^b \bmod m$，若有 $\gcd(a, m) = 1$ 则可以化为 $a^{b \bmod \varphi(m)} \bmod m$。

---

四、扩展欧拉定理

$$ a^b \equiv \begin{cases} a^b \bmod \varphi(m), & \gcd(a, m) = 1, \\ a^b, & \gcd(a, m) \neq 1, b < \varphi(m), \pmod{m} \\ a^{(b \bmod \varphi(m)) + \varphi(m)}, & \gcd(a, m) \neq 1, b \geq \varphi(m). \end{cases} $$

以 $2^b \bmod 20$ 为例，它会呈现混循环结构：

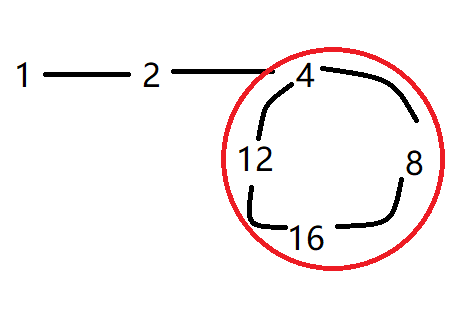
扩欧的意思就是把次幂强行扔进这个循环周期，减少运算次数。
注意当 $\gcd(a, m) \not=1$ 的时候指数不能 $+\varphi(m)$。
hack: a = 2, b = 1, mod = 4。

Code.
扩欧应用：CF906D。
扩欧应用 2：洛谷 P3747 六省联考 2017 相逢是问候。

---

五、阶

通过欧拉定理我们知道，若 $\gcd(a, m) = 1$，则有 $a^{\varphi(m)} \equiv 1 \pmod m$。
现在我们想知道，令 $a^x \equiv 1 \pmod m$ 的最小正整数是多少？

若 $\gcd(a,m) = 1$，令 $a^x \equiv 1 \pmod m$ 的最小正整数 $x$ 被称作 $a$ 模 $m$ 的阶，记为 $\text{ord}_m(a)$。

显然地，$\text{ord}_m(a) ~ | ~ \varphi(m)$。因为现在相当于找比 $\varphi(m)$ 更小的循环节，使得循环之后又变成 $1$，因此前者必定是后者的因子。

解法 1

枚举 $\varphi(m)$ 的所有因子，然后暴力快速幂判断取模是否为 $1$。

解法 2

反过来想，若 $a^t \equiv 1 \pmod m$，则一定有 $\text{ord}_m(a) ~|~ t$。
所以考虑令 $t=\varphi(m)$，然后将 $t$ 分解质因数，对于每个质因数能除就除。
分解后至多有 $\log(m)$ 个质因子，还要快速幂 $O(\log m)$ 验证，因此如果已知 $m$ 的质因数分解，阶可以在 $O(\log^2 m)$ 的复杂度内求出。

---

六、原根

若 $a$ 模 $m$ 的阶等于 $\varphi(m)$，则称 $a$ 为 $m$ 的原根。

例如 $3$ 是 $7$ 的原根（$1 \to 3 \to 2 \to 6 \to 4 \to 5 \to 1, \varphi(7) = 6$）。

1. 原根是否存在

$m$ 有原根当且仅当 $m=2,4,p^{\alpha},2p^{\alpha}$，其中 $p$ 是奇素数。

重点是：素数有原根。

2. 判断 $a$ 是否为 $m$ 的一个原根

其实可以类比上面求阶的过程。
相当于是 $\varphi(m)$ 必须是 $a$ 的阶（最小循环节），因此只需要找是否有更小的循环节即可。
具体地，还是对 $\varphi(m)$ 分解质因数，对于所有 $k$ 个质因数，若 $a^{\frac{\varphi(m)}{pi}} \equiv 1 \pmod m$，说明存在更小的循环节，所以 $a$ 不是 $m$ 的原根。

3. 找一个数的所有原根 & 原根个数

事实上，一个数 $m$ 的原根在 $[2,m-1]$ 内分布较为随机，因此直接暴力查范围内每个数是否是它的原根即可，复杂度 $O(m \log^2 m)$。
我们有更优的做法（需要基于下面的第 4 点）：

• 先求出一个原根 $g$。
• 算出 $g$ 的所有幂次 $g^0, g^1, g^2, \dots, g^{\varphi(m) - 1}$，此时循环的环长为 $\varphi(m)$。
• 考虑 $g^k$ 是不是原根？相当于是从起点开始，在环上每一步跳的距离是 $k$，要走遍所有点才是原根（否则阶比 $\varphi(m)$ 小，更早循环一周就不是原根）。
• 在环上经过所有点，相当于是 $\gcd(k, \varphi(m)) = 1$。
• 因此一个数 $m$ 的原根数量为 $\varphi(\varphi(m))$，即先搞出环长，再考虑在环上跳。
• 这样只需要求出一个原根 $g$，就只需要使用 $n$ 次 $\gcd$ 即可，复杂度更优。
• 寻找最小原根复杂度约为 $O(\log m)$。

Code.

4. 原根的重要性

设 $g$ 是 $m$ 的一个原根。
则有 $g^0, g^1, \dots g^{\varphi(m)-1}$ 在模 $m$ 意义下两两不同，因为至少要 $g^{\varphi(m)}$ 才能形成一个周期回到 $1$。
并且它们和 $m$ 互质。

然而，由于 $[1,m]$ 中恰好有 $\varphi(m)$ 个数与 $m$ 互质，因此 $\{ g^0, g^1, \dots g^{\varphi(m)-1} \}$ 恰好是所有与 $m$ 互质的数。
特殊地，若 $m$ 是质数，则有 $\{ g^0, g^1, \dots g^{m-2} \}$ 恰好对应 $[1,m-1]$ 的所有数。

七、BSGS 算法

给定一个质数 $p$，以及一个整数 $a$，一个整数 $b$，现在要求你计算一个最小的非负整数 $x$，满足 $a^x \equiv b \pmod p$。

使用 BSGS 并不要求模数是质数，只需要 $\gcd(a,p) = 1$ 即可。
BSGS 算法解决这一问题的核心思想是折半搜索和分块。
首先根据欧拉定理，如果存在解 $x$，那么 $x \in [0,p)$，因为再往上就绕一圈进入循环了。
令 $T=\lceil \sqrt{p} \rceil$，然后强行把 $x$ 拆成 $x=iT-j$，这样 $i,j \in [1,T]$。

$$a^x \equiv b \pmod p$$
$$a^{iT-j} \equiv b \pmod p$$
$$a^{iT} \equiv b \times a^j \pmod p$$

考虑暴力枚举 $i,j$，复杂度仍然为 $O(p)$，但是如果只枚举其一呢？
用哈希表存储 $b \times a^j$ 的结果，然后再单独扫一遍左边 $a^{iT}$，查询右边是否存在对应的 $j$。
哈希表可以用 unordered_map 实现。

Code.

BSGS 应用：SDOI2013 随机数生成器。
BSGS 结合原根的应用：CF1106F。

八、ExBSGS 算法

BSGS 算法只能解决 $\gcd(a,p)=1$ 的问题。
对于 $\gcd(a,p) \not= 1$ 的情况，考虑把它强行变为可以用 BSGS 的情况，即通过转化使得 $\gcd(a,p) = 1$。

$$a^x \equiv b \pmod p$$

令 $g_1 = \gcd(a,p)$，两边（模数也要）同时 $\div g_1$：

$$\frac{a}{g1} a^{x-1} \equiv \frac{b}{g_1} \pmod {\frac{p}{g_1}}$$

但是 $g_2 = \gcd(a,\frac{p}{g_1})$ 不一定为 $1$，所以还要继续 $\div g_2$：

$$\frac{a^2}{g_1g_2} a^{x-2} \equiv \frac{b}{g_1g_2} \pmod {\frac{p}{g_1g_2}}$$

这样一直 $\div g_i$，令 $G=\prod\limits_{i=1}^{k} g_i$，直到 $\gcd(a, \frac{p}{G}) = 1$ 停止：

$$\frac{a^k}{G} a^{x-k} \equiv \frac{b}{G} \pmod {\frac{p}{G}}$$

由于 $\gcd(a, \frac{p}{G}) = 1$，所以 $\gcd(a^k,\frac{p}{g}) = 1$，因此逆元存在：

$$a^{x-k} \equiv \frac{b}{G} \times ( \frac{a^k}{G} ) ^{-1} \pmod {\frac{p}{G}}$$

此时就可以使用 BSGS 了。
注意使用 BSGS 之前需要特判 $x \leq k$ 的情况。

Code.

九、N 次剩余（Easy Version）

解方程 $x^n \equiv k \pmod p$，其中 $x \in [0,p-1]$，且 $p$ 是质数。

把 BSGS 的底数和指数互换了？但我们仍然只会求解形如 $a^x \equiv b \pmod p$ 的问题。
那就考虑用原根转化，由于 $p$ 是质数，先求出它的原根是 $g$，因此 $\{g^0, g^1, g^2, \dots, g^{p-2} \} = \{1, 2, \dots, p-1\}$。
假设 $x = g^t$，$k = g^b$，则现在需要求解 $tn \equiv b \pmod {m-1}$，这可以用 exgcd 求解。
而 $b$ 的计算可以使用 BSGS 在 $O(\sqrt{p})$ 的复杂度内解决。

其实中间可以插播一条 Medium Version（BZOJ2019 数论之神）。

十、N 次剩余（Hard Version）

解方程 $x^n \equiv k \pmod m$，其中 $x \in [0,m-1]$，不保证 $m$ 是质数，输出解的数量和所有可能解。

前面的几乎全部知识点综合 QwQ。

好的，我们曾经在 ExLucas 那里红温了半天，现在考虑用相同的套路解决 $m$ 不是质数的 N 次剩余：
将 $m$ 分解质因数：$m = \prod\limits_{i=1}^{\omega} p_i^{\alpha_i}$，然后分别对每个子问题求解 $x^n \equiv k \pmod {p_i^{\alpha_i}}$，最后再想怎么去合并这些答案。

---

为什么要分解成对质数幂取模的形式？

1. 在 ExLucas 中，最后需要使用 CRT 合并答案，因此要求每个子问题的模数是两两互质的。
2. 本题保证方程 $x^n \equiv k \pmod {p_i^{\alpha_i}}$ 在 $[0,p_i^{\alpha_i})$ 的解数 $\leq 10^6$。
3. 对于此题，更重要的一点是：奇质数幂有原根。

回顾 $m$ 为质数的情况，由于质数有原根，所以我们才能通过原根 $g$ 和 BSGS 降幂，化简为 exgcd 的形式。
然而，$2^{\alpha}$ 并不一定有原根，因此我们考虑按照 $p_i$ 是否为 $2$ 进行分类。

接下来考虑求解 $x^n \equiv k \pmod {p^\alpha}$，$p,\alpha$ 的下标 $i$ 就不写了。

分讨

$k=0$

先考虑一个简单的 Case 是 $k=0$。

即 $x^n \equiv 0 \pmod {p^\alpha}$，$p^\alpha ~|~ x^n$。
可以把 $x$ 表示成 $p$ 的次幂的形式：$x = p^{t}$，则 $p^\alpha ~|~ p^{nt}$，此时只要求 $nt \geq \alpha$。
所以此时答案为 $p^{\lceil \frac{\alpha}{n} \rceil} ~|~ x$ 的 $x$。

$p \not=2, \gcd(k,p)=1$

此时 $p^\alpha$ 一定有原根，且由于 $k,p$ 互质所以 $k$ 一定可以被表示为原根的次幂。
假设 $x \equiv g^a \pmod {p^\alpha}, k \equiv g^b \pmod {p^\alpha}$。
$b$ 可以用 BSGS 求解，$\varphi(p^\alpha)$ 是好算的，接下来就是解线性同余方程：$na \equiv b \pmod {\varphi(p^\alpha)}$，exgcd 即可。

然后要求出 $a$ 的所有可行解，参见 OI-Wiki 线性同余方程。
至于 $x \equiv g^a \pmod {p^\alpha}$ 快速幂一下就好了。

$p \not=2, \gcd(k, p) \not= 1$

虽然原根仍然存在，但此时不能通过原根的次幂表示 $k$。
我们希望它变成互质的形式，这样才能做 BSGS 并用原根解决问题。

因此考虑先把公因数提出来，由于模数是 $p$ 的次幂，因此公因数也只能是 $p$ 的次幂。
设 $x = t_1 p^{r_1}, k = t_2 p^{r_2}$，代入则有：$t_1 ^n p^{r_1n} \equiv t_2 p^{r_2} \pmod {p^\alpha}$。
因为已经特判过 $k=0$ 的情况，因此这里 $k \not= 0$，也就有 $r_1n = r_2 \lt \alpha$。
考虑方程两边（模数也要）同除 $p^{r_2}$，则方程变为：$t_1^n \equiv t_2 \pmod {p^{\alpha - r_2}}$。
此时有 $\gcd(t_2, p^{\alpha - r_2}) = 1$，可以用前一个直接求出所有满足条件的 $t_1$。

要求出所有解？
这里有 $t_1 \in [0,p^{\alpha - r_2})$，给 $t_1$ 不断加上 $p^{\alpha - r_2}$ 也可以得到满足条件的解，但 $t_1 \times p^{r_1}$ 不能超过 $p^{\alpha}$，因此 $t_1$ 的实际范围是 $[0, p^{\alpha - r_1})$。
每次加上 $p^{\alpha - r_2}$，上界是 $p^{\alpha - r_1} - 1$，因此最多加 $p^{r_2 - r_1} - 1$ 次。

$p = 2, \alpha \leq 2$

此时 $p^{\alpha} = 2 / 4$，存在原根，且之前算的时候也只用到了原根的性质，不需要其它任何条件。
因此这个情况可以直接和上面的一起处理。

$p = 2, \alpha \gt 2$

不太会分析，学了一下一种很牛的做法，但是注意力很抽象，惊为天人。

$$5^{2^{\alpha - 3}} \equiv 2^{\alpha - 1} + 1 \pmod {2^{\alpha}}$$
这个式子很魔怔，考虑归纳证明：

• 当 $\alpha = 3$，式子显然成立。
• 当 $\alpha \gt 3$，若 $\alpha - 1$ 是成立的，则将同余式两边同时平方，即可证明其成立。

然后有一个更为逆天的观察：$5$ 在模 $2^\alpha$ 意义下的的阶为 $2^{\alpha - 2}$。

证：
先将上面那个式子 $5^{2^{\alpha - 3}} \equiv 2^{\alpha - 1} + 1 \pmod {2^{\alpha}}$ 两边平方，得到 $5^{2^{\alpha - 2}} \equiv 1 \pmod {2^{\alpha}}$。
由于这是恒成立的，因此 $5$ 在模 $2^\alpha$ 意义下的阶必须要 $\leq 2^{\alpha - 2}$，否则阶就是 $2^{\alpha - 2}$ 了。
然后考虑阶的下界。
如果存在 $5^{2^i} \equiv 1 \pmod {2^{\alpha}}$，那么再对两边同时平方就有 $\forall j \gt i, 5^{2^j} \equiv 1 \pmod {2^{\alpha}}$。
由于 $5^{2^{\alpha - 3}} \not \equiv 1 \pmod {2^{\alpha}}$，因此阶必须 $\gt 2^{\alpha - 3}$。

根据欧拉定理，由于 $\gcd(5, 2^\alpha) = 1$，且 $\varphi(2^\alpha) = 2^{\alpha - 1}$，所以 $5^{2^{\alpha - 1}} \equiv 1 \pmod {2^\alpha}$，即阶必须是 $2^{\alpha - 1}$ 的因数，只能含有因子 $2$。
前面已证 $2^{\alpha - 3} \lt$ 阶 $\leq 2^{\alpha - 2}$，所以阶只能是 $2^{\alpha - 2}$。

---

考虑重新定义一下原根在本题的用途。
在之前使用原根的时候，我们想到的是令原根为 $g$，且 $g$ 的次幂可以不重复地映射到与模数互质的数的集合，然后降幂做同余方程。
由于 $2^{\alpha - 2}$ 是 $5$ 在模 $2^\alpha$ 意义下的阶，因此根据阶的性质，当 $i \in [0,\alpha - 2)$ 时 $5^i \bmod 2^\alpha$ 是不重复的。
那么 $5$ 和原根有相似的性质，能否用它代替原根完成降幂？

然后就是很 bt 的注意力惊人了。

构造 $(-1)^a 5^b \equiv x \pmod {2^{\alpha}}$，其中 $a \in [0,1], b \in [0, 2^\alpha - 2)$，$x$ 是奇数。
考虑对这个构造方程求解，首先不可能存在 $(a_1, b_1) \not= (a_2, b_2)$ 使它们解出来的 $x$ 相等，易证。
$x$ 有 $2^{\alpha - 1}$ 种取值，$(a,b)$ 二元组总共有 $2 \times 2^{\alpha - 2} = 2^{\alpha - 1}$ 种取值，且不同的 $(a,b)$ 不会对应相同的 $x$，因此 $(a,b)$ 和 $x$ 是一一对应匹配的。
即方程有唯一解。
然后再对 $k$ 分类讨论求解：

$k$ 是偶数

此时相当于 $\gcd(k, 2) \not= 1$，直接合并到之前的情况即可。

$k$ 是奇数

接下来就是很牛的事情了。
考虑和之前一样，对 $k$ 做一件类似于原根降幂的事情。
如果我们可以把 $k$ 表示为 $(a_2,b_2)$ 二元组，那么就有：$a_1n \equiv a_2 \pmod 2, b_1n \equiv b_2 \pmod {2^{\alpha - 2}}$，类似地做 exgcd 即可。
但现在没法求 $(a_2, b_2)$，事实上直接枚举 $a_2$ 用 BSGS 求 $b_2$ 即可。

---

Combine

终于结束了又臭又长的分讨。
现在要合并每一个子问题的答案，由于题目保证了多测的总答案数 $\leq 10^6$，所以可以 dfs 暴力合并。
具体地，暴力枚举每一个子问题选择哪一个解，然后用 CRT 把这些东西给揉到一起取即可。

Code

#include <bits/stdc++.h>
#define int long long
#define PII pair<int, int>
using namespace std;
const int INF = 1e15;

int qmi(int a, int k, int mod) {
    int res = 1 % mod;
    while (k) {
        if (k & 1) res = res * 1ll * a % mod;
        a = a * 1ll * a % mod, k >>= 1;
    }
    return res;
}

vector< PII > D; int Cnt;
void divide(int x) {
    D.clear();
    for (int i = 2; i <= x / i; i++) {
        if (x % i) continue;
        int c = 0;
        while (x % i == 0) x /= i, c++;
        D.push_back({i, c});
    }
    if (x > 1) D.push_back({x, 1});
}

int gcd(int a, int b) { return b ? gcd(b, a % b) : a; }
int exgcd(int a, int b, int &x, int &y) {
    if (!b) { x = 1, y = 0; return a; }
    int d = exgcd(b, a % b, y, x);
    y -= (a / b) * x;
    return d;
}

int pr[30], tot = 0;
int get_phi(int n) {    // get phi n
    int res = n, x = n; tot = 0;
    for (int i = 2; i <= x / i; i++) {
        if (x % i) continue;
        res = res / i * (i - 1);
        while (x % i == 0) x /= i;
    }
    if (x > 1) res = res / x * (x - 1);

    x = res;
    for (int i = 2; i <= x / i; i++) {
        if (x % i) continue;
        pr[++tot] = i;
        while (x % i == 0) x /= i;
    }
    if (x > 1) pr[++tot] = x;
    return res;
}
bool check_gen(int x, int phi, int pa) {
    if (qmi(x, phi, pa) != 1) return 0;
    for (int i = 1; i <= tot; i++)
        if (qmi(x, phi / pr[i], pa) == 1) return 0;
    return 1;
}
int get_gen(int p, int alpha, int pa, int phi) {    // 求 p^alpha = pa 的一个原根（保证存在）
    for (int i = 1; i < pa; i++)
        if (check_gen(i, phi, pa)) return i;
    return 0;
}

unordered_map<int, int> mp;
int BSGS(int a, int b, int p) { // a^x = b   mod p
    mp.clear(), b %= p;
    int mul = 1, now = 1, B = sqrt(p) + 1;
    for (int i = 0; i <= B; i++) {
        if (mul == b) return i;
        if (!mp.count(b * mul % p)) mp[b * mul % p] = i;
        if (i < B) mul = mul * a % p;
    }
    for (int j = 1; j <= B; j++) {
        now = now * mul % p;
        if (mp.count(now)) return j * B - mp[now];
    }
    return -1;
}

vector<int> solve(int n, int k, int p, int alpha) {
    int pa = qmi(p, alpha, INF); k %= pa;
    vector<int> res; res.clear();
    if (k == 0) {   // Easy Case
        int mi = ceil(alpha * 1.0 / n);
        int one = qmi(p, mi, INF), now = 0;
        while (now < pa) res.push_back(now), now += one;
        return res;
    }
    if (gcd(k, p) != 1) {   // 转化后变成互质情况
        int r1 = 0, r2 = 0, t2 = k;
        while (t2 % p == 0) t2 /= p, r2++;
        if (r2 % n) return res; // 由于 r1 * n = r2，所以需要保证 r2 是 n 的倍数
        r1 = r2 / n;
        vector<int> pre = solve(n, t2, p, alpha - r2);  // 求出 { t1 }
        int one = qmi(p, alpha - r2, INF);  // 每次加上 one
        int c = qmi(p, r2 - r1, INF) - 1;   // 加的次数 c
        int pr1 = qmi(p, r1, INF);  // 乘的系数
        for (int it : pre)
            for (int i = 0; i <= c; i++)
                res.push_back(it * pr1 % pa), it += one;
        return res;
    }
    if ((p == 2 && pa <= 4) || p != 2) {
        // p != 2 或 pa = 2/4 时的互质情况，pa 存在原根才能这么做
        int phi = get_phi(pa);
        int gen = get_gen(p, alpha, pa, phi);
        int b = BSGS(gen, k, pa);
        int x, y, d = exgcd(n, phi, x, y);  // x = n^(-1)  (mod phi)
        if (b % d) return res;  // 空，方程无解
        int mod = phi / d;
        int a = (x * (b / d) % mod + mod) % mod;
        int now = qmi(gen, a, pa), one = qmi(gen, mod, pa);
        while (a < phi) res.push_back(now), a += mod, (now *= one) %= pa;
        return res;
    } else {    // p == 2 && alpha >= 3
        int p2 = qmi(p, alpha - 2, INF);
        for (int a2 = 0; a2 <= 1; a2++) {
            int b2 = BSGS(5, (a2 == 0) ? k : (pa - k), pa);
            if (b2 == -1) continue; // BSGS 无解
            // a1 * n = a2 (mod 2)
            int xa, ya, da = exgcd(n, 2, xa, ya);
            if (a2 % da) continue;
            // b1 * n = b2 (mod 2^(alpha - 2) )
            int xb, yb, db = exgcd(n, p2, xb, yb);
            if (b2 % db) continue;

            int moda = 2 / da, modb = p2 / db;
            int a1 = (xa * (a2 / da) % moda + moda) % moda, b1 = (xb * (b2 / db) % modb + modb) % modb;

            while (a1 <= 1) {
                int a = (a1 == 0) ? 1 : -1, b = b1;
                int now = qmi(5, b, pa);
                int one = qmi(5, modb, pa);
                while (b < p2) {
                    res.push_back( ( (a * now) % pa + pa) % pa );
                    (now *= one) %= pa, b += modb;
                }
                a1 += moda;
            }
        }
        return res;
    }
}
vector<int> res[30], ans;

int inv(int n, int m) { int x, y, d = exgcd(n, m, x, y); return (x % m + m) % m; }
struct Mat_Crt {
    int a[30], b[30], m[30];
    int solve() {
        int Mul = 1, ans = 0;
        for (int i = 0; i < Cnt; i++) Mul *= b[i];
        for (int i = 0; i < Cnt; i++) m[i] = Mul / b[i];
        for (int i = 0; i < Cnt; i++) ( ans += ((__int128)m[i] * inv(m[i], b[i]) % Mul * a[i]) % Mul ) %= Mul;
        return ans;
    }
} CRT;

void dfs(int u) {
    if (u == Cnt) return ans.push_back(CRT.solve()), void();
    for (int it : res[u]) {
        CRT.a[u] = it, CRT.b[u] = qmi(D[u].first, D[u].second, INF);
        dfs(u + 1);
    }
}


int n, m, k;
void mian() {
    scanf("%lld%lld%lld", &n, &m, &k);
    divide(m), Cnt = D.size();
    // for (auto it : D) cout << it.first << ' ' << it.second << endl;
    for (int i = 0; i < Cnt; i++) {
        res[i] = solve(n, k, D[i].first, D[i].second);
        if (res[i].size() == 0) return puts("0"), void();
    }
    // for (int i = 0; i < Cnt; i++, puts(""))
    //     for (int it : res[i]) cout << it << ' ';
    ans.clear(), dfs(0);
    sort(ans.begin(), ans.end());
    printf("%d\n", (int)ans.size());
    for (int it : ans) printf("%d ", it);
    putchar('\n');
}

signed main() {
    int T; scanf("%d", &T);
    while (T--) mian();
    return 0;
}