题解
- 可以考虑将问题转换为求m个数都互不相同的概率
- 显然,对于所有人取数的可能性是2^nm
- 那么现在如果确定了1号的数,那么2与它不相同的概率求出2^n-1,3与1、2不相同的概率就是2^n-2...以此类推
- 一共有m-1个数
- 那么总共就是
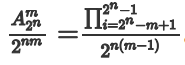
- 然后考虑将其约分,那么对于分母是只有2的质因数的,那么分子也只能约2
- 考虑能约多少个
- 对于任意一个1<=a<2^n,a与2^n-a的中2的次数相同
- 因此,只用求出(m-1)!的2的次数就好了
- 答案就是1-a/b=(b-a)/b
代码
1 #include <cstdio>
2 #include <cstring>
3 #include <iostream>
4 #include <cmath>
5 using namespace std;
6 const long long mo=1e6+3;
7 long long n,m;
8 long long ksm(long long a,long long b)
9 {
10 long long r=1;
11 for(;b;b>>=1,a=a*a%mo) if(b&1) r=r*a%mo;
12 return r;
13 }
14 int main()
15 {
16 scanf("%lld%lld",&n,&m);
17 if (log2(m)>n)
18 {
19 printf("1 1\n");
20 return 0;
21 }
22 long long a=ksm(2,n),down=ksm(a,m),up=1;
23 for (long long i=0;i<m;i++)
24 {
25 up=up*(a-i)%mo;
26 if (!up) break;
27 }
28 m--; long long k=n;
29 for (long long i=2;i<=m;i<<=1) k+=m/i;
30 down=down*ksm(500002,k)%mo;
31 up=up*ksm(500002,k)%mo;
32 printf("%lld %lld\n",(down-up+mo)%mo,down);
33 }
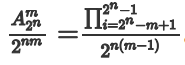


 浙公网安备 33010602011771号
浙公网安备 33010602011771号