[dp][组合数] Jzoj P4271 魔法阵

Description

帕秋莉·诺蕾姬，有着“不动的大图书馆” 的称号，擅长使用各种各样的属性魔法。
——《东方求闻史记》
一如既往地，帕秋莉在图书馆中研究着魔法。今天，她在研究一本魔法书中的法阵。
这个法阵可以看成是按下面的规则生成一个规模为n(n 为非负整数) 的图形：
1. 在直角坐标系xOy 中，画4 条线段：[(0,0), (2^n,0)], [(0, 0), (􀀀-2^n, 0)],[(0, 0), (0, 2^n)], [(0, 0), (0,-􀀀2^n)]。
2. 对于所有的i = 1, 2, ......, n，画两个正方形，一个以(0, 2^i), (0,-􀀀2^i),(2^i, 0), (􀀀-2^i, 0) 为顶点，另一个以(􀀀-2i-􀀀1,-2i-􀀀1),(􀀀-2i-􀀀1,2i-􀀀1), (􀀀2i-􀀀1,-2i-􀀀1)(􀀀2i-􀀀1,2i-􀀀1) 为顶点。
3. 画一个以(1, 0), (􀀀-1, 0), (0,-1), (0, 1) 为顶点的正方形。
比如，当n = 0 时的法阵是这样的：

当n = 2 时的法阵是这样的：

帕秋莉已经画出了这个巨大的法阵, 并且她能够同时控制k 种不同的属性元素。接下来，她要将这k 种元素分别依次灌注进法阵中的k 个不重叠不相交的三角形中，即这k 个三角形要灌注进不同的元素。这样，这个法阵就会被激活。
然而，灌注的方法有许多种。为了能最大限度地进行实验，帕秋莉想把所有的方法都实验一遍。而摆在她面前的问题是，总共有多少种不同的灌注方法呢？
注意，由于是法阵，看起来是中心对称或轴对称的两个三角形，也是实质不等同的。或者说，假如两个方案A 和B，只有通过旋转、翻转或二者组合才能使所有相同位置的三角形被灌注的元素相同，A 和B 仍然是不同的方案。只有本来所有相同位置的三角形被灌注的元素相同才算是相同的方案。
由于方法数会很大，帕秋莉只需要你输出模1,000,000,007(10^9 + 7) 的结果就可以了。
 

 

Input

输入文件magic.in。
一共一行两个整数n,k，意义如题中所述。

Output

输出文件magic.out。
一共一行一个整数res，表示灌注方案数模1,000,000,007(109 + 7) 得到的结果。

 

Sample Input

输入1：
0 0
输入2：
0 1
输入3：
0 2 
输入4：
1 1

Sample Output

输出1：
1
输出2：
8
输出3：
32
输出4：
32

 

Data Constraint

对于15% 的数据，k <= 1。
对于30% 的数据，k <= 2。
另外，有15% 的数据，满足n <= 2。
对于100% 的数据，0<= n <= 200，0<= k <= min(200, 8n + 4)。

 

 

题解

• 第一眼，看到题目，又是xjb乱搞的数论题
• 看了看数据范围，果断水k<=1的点，其实就是每次+24
• 题目大意：就是给你一个N，要你创造出一个

• 1. 在直角坐标系xOy 中，画4 条线段：[(0,0), (2^n,0)], [(0, 0), (􀀀-2^n, 0)],[(0, 0), (0, 2^n)], [(0, 0), (0,-􀀀2^n)]。
  2. 对于所有的i = 1, 2, ......, n，画两个正方形，一个以(0, 2^i), (0,-􀀀2^i),(2^i, 0), (􀀀-2^i, 0) 为顶点，另一个以(􀀀-2i-􀀀1,-2i-􀀀1),(􀀀-2i-􀀀1,2i-􀀀1), (􀀀2i-􀀀1,-2i-􀀀1)(􀀀2i-􀀀1,2i-􀀀1) 为顶点。
  3. 画一个以(1, 0), (􀀀-1, 0), (0,-1), (0, 1) 为顶点的正方形。

• 现在给这个正方形里的三角形染色，问有多少中不同的情况
• 对于图中的三角形，我们可以先做一个分类
• ①经过源点的三角形，后面统称源三角形
• ②不经过源点的三角形，一级三角形（只有一个三角形组成），二级三角形（只有两个三角形组成）。。。
• 其实没有其它三角形的组成了，不信的可以手画一下
• 可以考虑从极端的n=0开始
• 
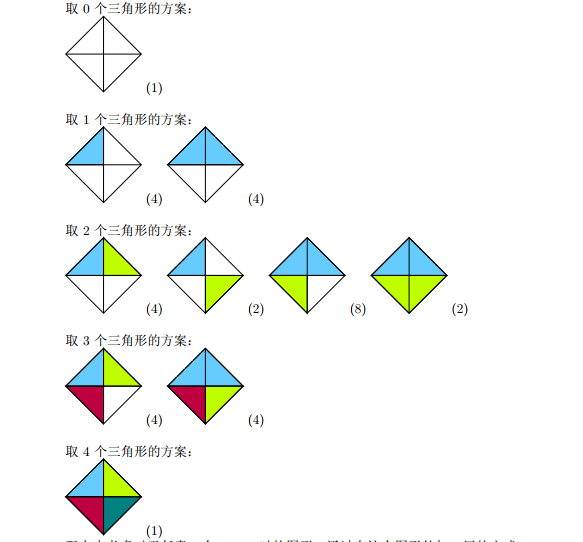
• 那我们现在可以考虑从i转移到i+1
• 那么转移后必定会出现源三角形、一级三角形、二级三角形
• 
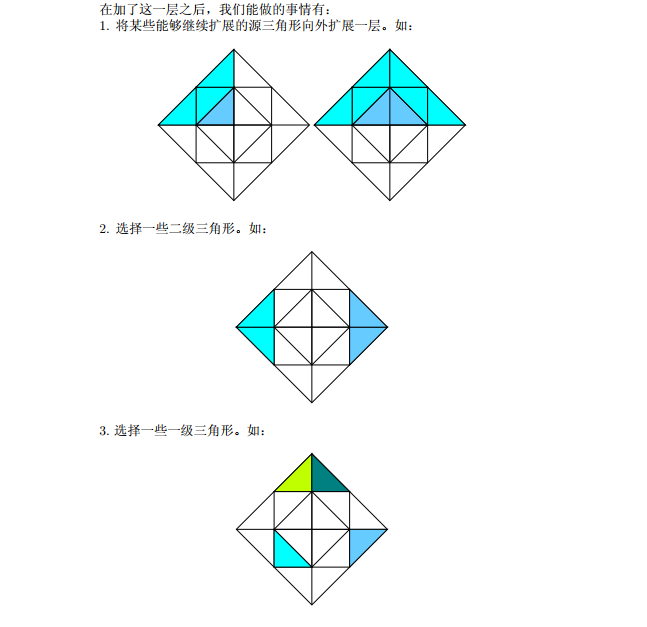
• 对于第i个正方形在忽略了不能拓展的三角形以后，都为形成一个较大的n=0的形状
• 那么拓展后的绝对会与上面n=0时的某一种方案同构
• 这样的话，我们就可以不用一下子求出当前第i个正方形选三角形的方案
• 可以考虑从小正方形每次向大正方形转移
• 可以用dp
• 设f[i][j][k]表示当前拓展到第i层，总共选了j个三角形，能够拓展的源三角形的形状为编号j（也就是以上10中同构方案的标号）的方案数
• 考虑如何转移
• 从上面可以知道源三角形拓展后可以成为另一种同构方案
• 那么可以枚举同构方案，判断两种情况是否可以拓展
• 对于答案肯定不只是有源三角形的方案数，还有一级三角形和二级三角形的方案数，那么怎么求？在循环里求吗？
• 那肯定会炸，知道对于一种形态，它们所拥有的一级三角形和二级三角形的个数必定是相同的
• 那么就可以手推直接打表加入数组里，我们用dt1[i]和dt2[i]来记录
• 表示从第i个形态方式，剩下的一级三角形和二级三角形的个数
• 现在再来考虑下对于一种形态可以转换到哪几种形态
• 
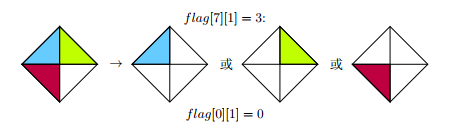
• 这个也像上面一样，直接手推出来，打表放入数组，用flag[i][j]记录
• 表示从第i种形态拓展到第j种形态的方案数
• 现在，就可以得出状态转移方程了
• f[i+1][j+s1+s2][label′]+f[i][j][label]×flag[label][label′]×C(s2,dt2[label′])×C(s1,dt1[label′])−2×s2→ f[i+1][j+s1+s2][label′]
• s1表示枚举当前加入多少个一级三角形，s2表示枚举加入多少个二级三角形，label表示拓展前的形态，label'表示拓展后的形态
• 注意一些边界情况：
• f[0][0][0] = 1,f[0][1][1] = 4 f[0][1][2] = 4,f[0][2][3] = 4 f[0][2][4] = 2,f[0][2][5] = 8 f[0][2][6] = 2,f[0][3][7] = 4 f[0][3][8] = 4,f[0][4][9] = 1
• 组合数就用杨辉三角来求就好了。。。
• 本蒟蒻太菜了，如果看不懂的详见题解

代码

#include<cstdio>
#include<iostream>
#include<algorithm>
using namespace std;
const long long mo=1000000007;
int boo[10][10]={{1,0,0,0,0,0,0,0,0,0},
                 {1,1,0,0,0,0,0,0,0,0},
                 {1,0,1,0,0,0,0,0,0,0},
                 {1,2,0,1,0,0,0,0,0,0},
                 {1,2,0,0,1,0,0,0,0,0},
                 {1,1,1,0,0,1,0,0,0,0},
                 {1,0,2,0,0,0,1,0,0,0},
                 {1,3,0,2,1,0,0,1,0,0},
                 {1,2,1,1,0,2,0,0,1,0},
                 {1,4,0,4,2,0,0,4,0,1}};
int dt1[10]={12,9,6,6,6,3,0,3,0,0},dt2[10]={4,2,1,1,0,0,0,0,0,0},n,k;
long long f[210][210][210],c[210][210],ans;
int main()
{
    freopen("magic.in","r",stdin);
    freopen("magic.out","w",stdout);
    scanf("%d%d",&n,&k); 
    c[0][0]=1;
    for (int i=1;i<15;i++)
    {
        c[i][0]=1;
        for (int j=1;j<=i;j++) c[i][j]=(c[i-1][j]+c[i-1][j-1])%mo;
    }
    f[0][0][0]=1; f[0][1][1]=4; f[0][1][2]=4; f[0][2][3]=4; f[0][2][4]=2; 
    f[0][2][5]=8; f[0][2][6]=2; f[0][3][7]=4; f[0][3][8]=4; f[0][4][9]=1;
    for (int i=0;i<n;i++)
        for (int j=0;j<10;j++)
            for (int p=0;p<=k;p++)
                if (f[i][p][j])
                    for (int q=0;q<10;q++)
                        if (boo[j][q])
                        {
                            int x=dt1[q],y=dt2[q];
                            for (int r=0;r+p<=k&&r<=y;r++)
                                for (int t=0;t+p+r<=k&&t<=x-2*r;t++)
                                    (f[i+1][t+p+r][q]+=(f[i][p][j]*c[y][r])%mo*c[x-2*r][t]*boo[j][q])%mo;
                        }
    for (int i=0;i<10;i++) ans=(ans+f[n][k][i])%mo;
    for (int i=1;i<=k;i++) ans=(ans*i)%mo;
    printf("%lld",ans);
    return 0;
}