题解
- 题目大意:当前有个小SB在(n,1)然后他要走到(1,1),他可以选择两种走法,一种是走到(x+1,y-1)不需要代价,一种是走到(x,(y+1)/2)需要
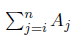 代价,问他需要的最小代价是多少
代价,问他需要的最小代价是多少
- 这种题一眼看到一般就是dp或这是最短路径问题
- 50%:显然可以用dp来做,设f[i][j]为走到(i,j)的最小代价
- 那么就有两种转移情况,不过这dp要倒着做,不然可以考虑跑多几次
- 100%:数组是有序的,所以在哈夫曼树上深度是递增不减
- 那么我们可以设f[i][j]为现在放入了下标比 i 小的所有节点,剩余的叶子节点有 j 个
- 按照题目我们就有两种情况可以走
- ①F[i+1][j−1],表示在剩下可放的节点中选一个来放第(i+1)个,不需要代价
- ②F[i][j∗2]+Σa[i+1][n],表示把剩下的j个叶子节点往下再扩展2个节点,需要为代价就是后缀和
- 其实就是50分的dp逆做,然后答案就是哈夫曼树的最小权值
- (其实这题就是合并果子,合并果子也是哈夫曼树求最小权值)
- 直接用优先队列做就好了
代码
1 #include <iostream>
2 #include <queue>
3 #include <cstdio>
4 using namespace std;
5 int T,n;
6 long long ans;
7 priority_queue<int,vector<int>,greater<int> >Q;
8 int main()
9 {
10 scanf("%d",&T);
11 while (T--)
12 {
13 scanf("%d",&n),ans=0;
14 for (int i=1,x;i<=n;i++) scanf("%d",&x),Q.push(x);
15 for (int i=n,x;i>1;i--) x=Q.top(),Q.pop(),x+=Q.top(),Q.pop(),ans+=x,Q.push(x);
16 printf("%lld\n",ans);
17 while (!Q.empty()) Q.pop();
18 }
19 }
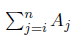 代价,问他需要的最小代价是多少
代价,问他需要的最小代价是多少

 浙公网安备 33010602011771号
浙公网安备 33010602011771号