Atcoder abc287_c Path Graph 题解

题目链接

传送门

题目大意

给定一个无向图，判断其是否是一条链。

思路分析

首先明确链的定义，这里引用题目中的描述。

当且仅当有一个序列 \((v_1, v_2, \dots, v_N)\) 是 \((1, 2, \dots, N)\) 的排列，并且满足以下条件时，才可以说一个有 \(N\) 个顶点、编号为 \(1, 2, \dots, N\) 的图是链：

• 对于所有 \(i = 1, 2, \dots, N-1\) ，有一条边连接顶点 \(v_i\) 和 \(v_{i+1}\) 。
• 若整数 \(i\) 和 \(j\) 满足 \(1 \leq i, j \leq N\) 和 \(|i - j| \geq 2\) ，则没有边连接顶点 \(v_i\) 和 \(v_j\) 。

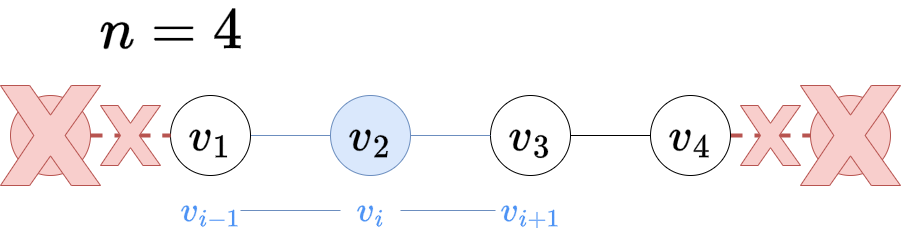
对于一条链，两个端点的度数为 \(1\)，其余每个点的度数为 \(2\)，分别连接 \(v_{i-1}\) 和 \(v_{i+1}\)，即每个点的度数都 \(\le 2\)。所以，如果有一个点的度数大于 \(2\)，这个无向图肯定就不是链。同时，链的边数一定等于顶点数减 \(1\)。在加入这两个特判后，这个图同时应保证连通。我们可以使用 dfs、bfs 或并查集判断是否连通。总时间复杂度 \(O(n)\)。

代码精讲

#include<bits/stdc++.h>
using namespace std;

const int N=2e5+10;
int n,m;
vector<int> f[N];
bool vis[N];
queue<int> q;

int main(){
    scanf("%d%d",&n,&m);
    for (int i=1;i<=m;++i){
        int u,v;
        scanf("%d%d",&u,&v);
        f[u].push_back(v);
        f[v].push_back(u);
    }
    if (m!=n-1){ // 判边数
        printf("No");
        return 0;
    }
    for (int i=1;i<=n;++i){ // 判度数
        if (f[i].size()>2){
            printf("No");
            return 0;
        }
    }
    q.push(1),vis[1]=1; // bfs 判连通
    while (!q.empty()){
        int u=q.front();
        q.pop();
        int l=f[u].size();
        for (int i=0;i<l;++i){
            int v=f[u][i];
            if (!vis[v]) q.push(v),vis[v]=1;
        }
    }
    for (int i=1;i<=n;++i){
        if (!vis[i]){
            printf("No");
            return 0;
        }
    }
    printf("Yes");
    return 0;
}