CF Gym103536B Troubles 做题记录

前置芝士：李超线段树。

题目大意

给定 \(N\) 个点，每个点 \(i\) 有两个属性 \(x_i\) 和 \(y_i\)。需要将这些点划分为若干组（每组非空），对于每组，定义其代价为组内所有点中 \(x_i\) 的最大值与 \(y_i\) 的最大值的乘积。总代价为所有组的代价之和。求总代价的最小值。

思路

首先如果有一组 \((i,j)\) 使得 \(x_i<x_j\) 且 \(y_i<y_j\)，那么可以不用考虑 \(i\) 的存在，因为如果选了 \(j\) 顺便把 \(i\) 选到一组就好了。

因为有两维的 \(\max\) 不好做，所以我们先按一维 \(x\) 排序，然后就可以 dp 了，现在应该是长这样：

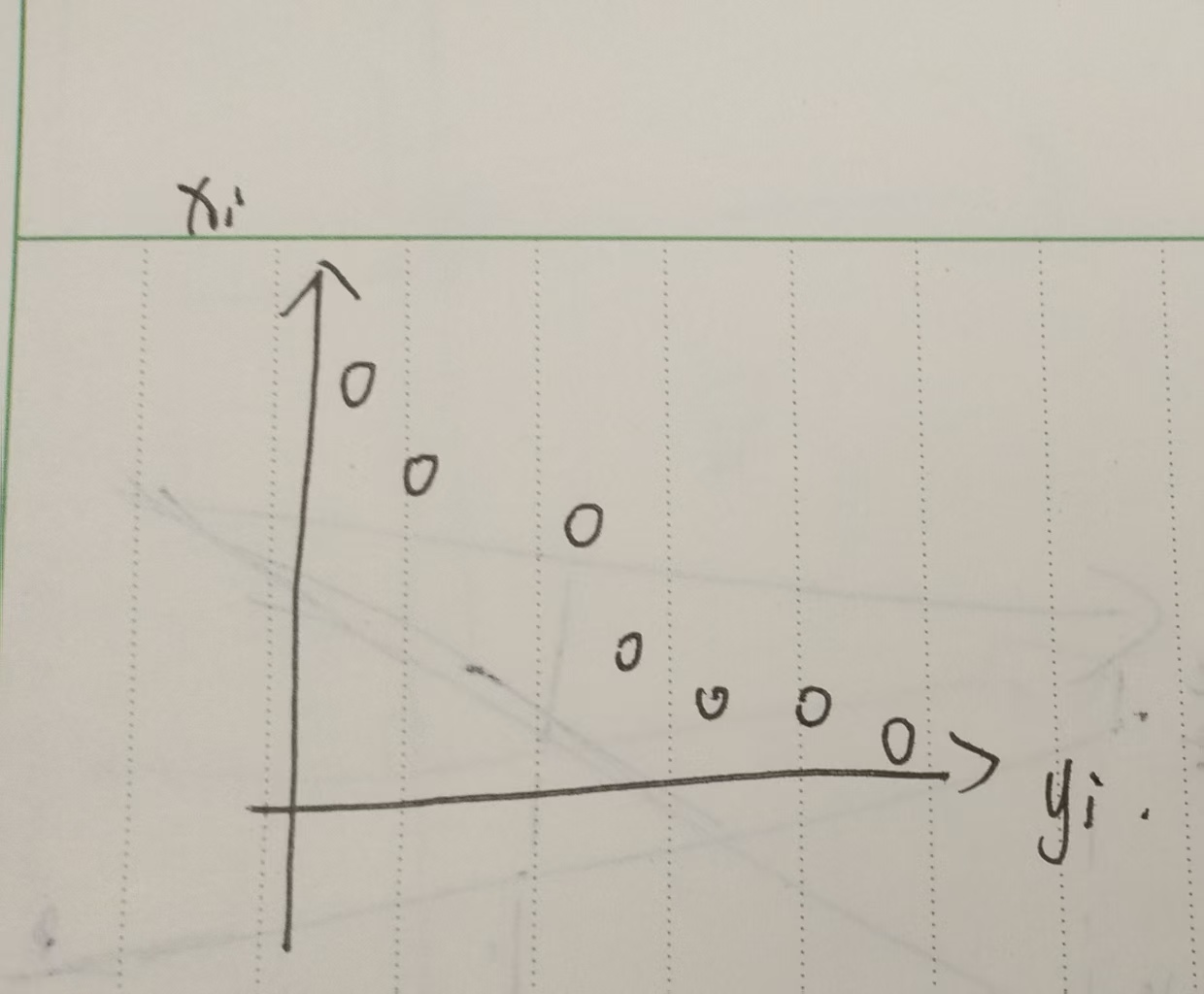
设 \(f_{i}\) 表示处理到第 \(i\) 位时的最小花费，那么有 \(dp_i=\min_{j\le i}\ dp_{j-1}+a_j\times b_i\)。我不会维护凸包，但是这个形式很类似 \(y=kx+b\) 的形式，考虑用李超线段树来维护这个东西的最小值。

但是注意到 \(x_i,y_i\) 的值域其实有 \(10^7\)，所以李超树不要对 \([1,10^7]\) 建树，而是要对 \([1,n]\) 建树，其中第 \(i\) 的位置表示 \(y_i\)（人话就是离散化，虽然动态开点也可以写 qwq）。

时间复杂度：\(O(n\log n)\)。

点击查看代码

#include<bits/stdc++.h>

#define int ll
#define pii pair<int,int> 
#define pll pair<long long,long long> 
#define ll long long
#define i128 __int128

#define mem(a,b) memset((a),(b),sizeof(a))
#define m0(a) memset((a),0,sizeof(a))
#define m1(a) memset(a,-1,sizeof(a))
#define lb(x) ((x)&-(x))
#define lc(x) ((x)<<1)
#define rc(x) (((x)<<1)|1)
#define pb(G,x) (G).push_back((x))
#define For(a,b,c) for(int a=(b);a<=(c);a++)
#define Rep(a,b,c) for(int a=(b);a>=(c);a--)
#define in1(a) a=read()
#define in2(a,b) a=read(), b=read()
#define in3(a,b,c) a=read(), b=read(), c=read()
#define in4(a,b,c,d) a=read(), b=read(), c=read(), d=read()
#define fst first 
#define scd second 
#define dbg puts("IAKIOI")

using namespace std;

int read() {
	int x=0,f=1; char c=getchar();
	for(;c<'0'||c>'9';c=getchar()) f=(c=='-'?-1:1); 
	for(;c<='9'&&c>='0';c=getchar()) x=(x<<1)+(x<<3)+(c^48);
	return x*f;
}
void write(int x) { if(x>=10) write(x/10); putchar('0'+x%10); }

const int mod = 998244353;
int qpo(int a,int b) {int res=1; for(;b;b>>=1,a=(a*a)%mod) if(b&1) res=res*a%mod; return res; }
int inv(int a) {return qpo(a,mod-2); }

#define maxn 300500

int n;
pii p[maxn]; int top1,top2,x[maxn],y[maxn];
pii a[maxn]; int siz;
int mx[maxn];
int disc(int qwq,int opt) {
	if(!opt) return lower_bound(x+1,x+top1+1,qwq)-x;
	else return lower_bound(y+1,y+top2+1,qwq)-y;
}

struct fx {
	int k,b;
	int calc(int val) {
		return k*val+b;
	}
}f[maxn];

struct LC_Tr {
	int ind[maxn<<2];
	void add(int idx,int l,int r,int k) {
		if(!ind[idx]) return ind[idx]=k,void();
		int mid=l+r>>1;
		if(f[k].calc(y[mid])<f[ind[idx]].calc(y[mid])) swap(k,ind[idx]);
		if(f[k].calc(y[l])<f[ind[idx]].calc(y[l])) add(lc(idx),l,mid,k);
		if(f[k].calc(y[r])<f[ind[idx]].calc(y[r])) add(rc(idx),mid+1,r,k);
		return ;
	}
	int query(int idx,int l,int r,int k) {
		if(l==r) return f[ind[idx]].calc(y[k]);
		int mid=l+r>>1,res=0;
		if(k<=mid) res=query(lc(idx),l,mid,k);
		else res=query(rc(idx),mid+1,r,k);
		return min(res,f[ind[idx]].calc(y[k]));
	}
}Tr;

int dp[maxn];

void work() {
	in1(n);
	For(i,1,n) in2(p[i].first,p[i].second),x[i]=p[i].first,y[i]=p[i].second;
	sort(x+1,x+n+1); top1=unique(x+1,x+n+1)-x-1;
	sort(y+1,y+n+1); top2=unique(y+1,y+n+1)-y-1;
	sort(p+1,p+n+1);    n=unique(p+1,p+n+1)-p-1;
	sort(p+1,p+n+1,greater<pii>());
	For(i,1,n) mx[disc(p[i].first,0)]=max(mx[disc(p[i].first,0)],p[i].second);
	Rep(i,top1-1,1) mx[i]=max(mx[i],mx[i+1]); 
	For(i,1,n) if(mx[disc(p[i].first,0)]==p[i].second) a[++siz]=p[i]; 
//	cout<<siz<<'\n';
//	For(i,1,siz) cout<<a[i].first<<' '<<a[i].second<<'\n';
	f[0]={(ll)1e9,(ll)1e9};
	For(i,1,siz) {
//		cout<<"qwq"<<a[i].first<<' '<<a[i].second<<'\n';
		f[i].k=a[i].first,f[i].b=dp[i-1];
		Tr.add(1,1,top2,i);
		dp[i]=Tr.query(1,1,top2,disc(a[i].second,1));
	}
	cout<<dp[siz]<<'\n';
}

signed main() {
//	freopen("data.in","r",stdin);
//	freopen("myans.out","w",stdout);
//	ios::sync_with_stdio(false); 
//	cin.tie(0); cout.tie(0);
	double stt=clock();
	int _=1;
//	_=read();
//	cin>>_;
	For(i,1,_) {
		work();
	}
	cerr<<"\nTotal Time is:"<<(clock()-stt)*1.0/1000<<" second(s)."<<'\n';
	return 0;
}