Codeforces Round 1045 (Div. 2) 比赛记录

偶遇神秘构造题,拼尽全力无法战胜。
A
题目大意
有一个长度为 \(n\) 的序列,你要先后进行染色一个长度为 \(a\) 的红色区间和一个长度为 \(b\) 的蓝色区间。
大致思路
首先如果蓝色比红色长,红色等于没有效果,因为可以被蓝色完全覆盖,然后观察 \(b\) 与 \(n\) 的奇偶性,如果相同即可染色。如果蓝色没有红色长,那么 \(a\) 和 \(b\) 的奇偶性都要与 \(n\) 相同,形成一个红色中间夹蓝色的方案。
代码
https://codeforces.com/contest/2134/submission/335621422
点击查看代码
#include<bits/stdc++.h>
#define pii pair<int,int>
#define pll pair<long long,long long>
#define ll long long
#define i128 __int128
#define mem(a,b) memset((a),(b),sizeof(a))
#define m0(a) memset((a),0,sizeof(a))
#define m1(a) memset(a,-1,sizeof(a))
#define lb(x) ((x)&-(x))
#define lc(x) ((x)<<1)
#define rc(x) (((x)<<1)|1)
#define pb(G,x) (G).push_back((x))
#define For(a,b,c) for(int a=(b);a<=(c);a++)
#define Rep(a,b,c) for(int a=(b);a>=(c);a--)
#define in1(a) a=read()
#define in2(a,b) a=read(), b=read()
#define in3(a,b,c) a=read(), b=read(), c=read()
#define in4(a,b,c,d) a=read(), b=read(), c=read(), d=read()
#define fst first
#define scd second
#define dbg puts("IAKIOI")
using namespace std;
int read() {
int x=0,f=1; char c=getchar();
for(;c<'0'||c>'9';c=getchar()) f=(c=='-'?-1:1);
for(;c<='9'&&c>='0';c=getchar()) x=(x<<1)+(x<<3)+(c^48);
return x*f;
}
void write(int x) { if(x>=10) write(x/10); putchar('0'+x%10); }
const int mod = 998244353;
int qpo(int a,int b) {int res=1; for(;b;b>>=1,a=(a*a)%mod) if(b&1) res=res*a%mod; return res; }
int inv(int a) {return qpo(a,mod-2); }
#define maxn 200050
int n,a,b;
void work() {
in3(n,a,b);
if(b>=a&&(b&1)==(n&1)) return cout<<"YES\n",void();
if((a&1)!=(b&1)) return cout<<"NO\n",void();
if((a&1)!=(n&1)) return cout<<"NO\n",void();
cout<<"YES\n";
}
signed main() {
// freopen("data.in","r",stdin);
// freopen("myans.out","w",stdout);
// ios::sync_with_stdio(false);
// cin.tie(0); cout.tie(0);
double stt=clock();
int _=1;
_=read();
// cin>>_;
For(i,1,_) {
work();
}
cerr<<"\nTotal Time is:"<<(clock()-stt)*1.0/1000<<" second(s)."<<'\n';
return 0;
}
B
题目大意
有一个长度为 \(n\) 的序列 \(a_i\),你要在 \(k\) 次操作内对于每个元素加上不多于 \(k\) 次的 \(k\),使得 \(\gcd(a_1,a_2,\dots,a_n)>1\)。
大致思路
注意到题目给出无论何时均可以完成任务,从 \(k\) 次操作入手,不难想到使得每个数包含一个 \(k+1\) 的最大公因数。那么给每个数 \(+k\) 相当于给除以 \(k+1\) 的余数 \(-1\)。最后将序列里的每个数减到 \(0\) 即可。
代码
https://codeforces.com/contest/2134/submission/335634789
点击查看代码
#include<bits/stdc++.h>
#define int ll
#define pii pair<int,int>
#define pll pair<long long,long long>
#define ll long long
#define i128 __int128
#define mem(a,b) memset((a),(b),sizeof(a))
#define m0(a) memset((a),0,sizeof(a))
#define m1(a) memset(a,-1,sizeof(a))
#define lb(x) ((x)&-(x))
#define lc(x) ((x)<<1)
#define rc(x) (((x)<<1)|1)
#define pb(G,x) (G).push_back((x))
#define For(a,b,c) for(int a=(b);a<=(c);a++)
#define Rep(a,b,c) for(int a=(b);a>=(c);a--)
#define in1(a) a=read()
#define in2(a,b) a=read(), b=read()
#define in3(a,b,c) a=read(), b=read(), c=read()
#define in4(a,b,c,d) a=read(), b=read(), c=read(), d=read()
#define fst first
#define scd second
#define dbg puts("IAKIOI")
using namespace std;
int read() {
int x=0,f=1; char c=getchar();
for(;c<'0'||c>'9';c=getchar()) f=(c=='-'?-1:1);
for(;c<='9'&&c>='0';c=getchar()) x=(x<<1)+(x<<3)+(c^48);
return x*f;
}
void write(int x) { if(x>=10) write(x/10); putchar('0'+x%10); }
const int mod = 998244353;
int qpo(int a,int b) {int res=1; for(;b;b>>=1,a=(a*a)%mod) if(b&1) res=res*a%mod; return res; }
int inv(int a) {return qpo(a,mod-2); }
#define maxn 200050
int n,k;
int a[maxn],x[maxn];
void work() {
in2(n,k);
For(i,1,n) in1(a[i]),x[i]=a[i]%(k+1);
if((k&1)) {
For(i,1,n) if(a[i]&1) a[i]+=k;
For(i,1,n) cout<<a[i]<<' ';
puts(""); return ;
}
For(i,1,n) a[i]+=k*(x[i]);
For(i,1,n) cout<<a[i]<<' '; puts("");
}
signed main() {
// freopen("data.in","r",stdin);
// freopen("myans.out","w",stdout);
// ios::sync_with_stdio(false);
// cin.tie(0); cout.tie(0);
double stt=clock();
int _=1;
_=read();
// cin>>_;
For(i,1,_) {
work();
}
cerr<<"\nTotal Time is:"<<(clock()-stt)*1.0/1000<<" second(s)."<<'\n';
return 0;
}
C
题目大意
给定一个由非负整数组成的数组 \(a = [a_1, a_2, \ldots, a_n]\),其中数组索引从 1 开始。如果对于每一个长度至少为 2 的子数组(子数组中的元素保留其在原数组中的索引位置),原数组中偶数索引(即索引 \(2, 4, 6, \ldots\))的元素之和大于或等于奇数索引(即索引 \(1, 3, 5, \ldots\))的元素之和,则该数组被称为好数组。
在一次操作中,可以将数组中的任意元素减少 1(操作后元素必须保持非负)。目标是求出使数组 \(a\) 变为好数组所需的最小操作次数。
大致思路
注意到只用保证偶数位旁边的数字之和小于等于该位,所以贪心的先减少后面的(但是要保持非 \(0\)),然后在减当前偶数位。
代码
https://codeforces.com/contest/2134/submission/335641413
点击查看代码
#include<bits/stdc++.h>
#define int ll
#define pii pair<int,int>
#define pll pair<long long,long long>
#define ll long long
#define i128 __int128
#define mem(a,b) memset((a),(b),sizeof(a))
#define m0(a) memset((a),0,sizeof(a))
#define m1(a) memset(a,-1,sizeof(a))
#define lb(x) ((x)&-(x))
#define lc(x) ((x)<<1)
#define rc(x) (((x)<<1)|1)
#define pb(G,x) (G).push_back((x))
#define For(a,b,c) for(int a=(b);a<=(c);a++)
#define Rep(a,b,c) for(int a=(b);a>=(c);a--)
#define in1(a) a=read()
#define in2(a,b) a=read(), b=read()
#define in3(a,b,c) a=read(), b=read(), c=read()
#define in4(a,b,c,d) a=read(), b=read(), c=read(), d=read()
#define fst first
#define scd second
#define dbg puts("IAKIOI")
using namespace std;
int read() {
int x=0,f=1; char c=getchar();
for(;c<'0'||c>'9';c=getchar()) f=(c=='-'?-1:1);
for(;c<='9'&&c>='0';c=getchar()) x=(x<<1)+(x<<3)+(c^48);
return x*f;
}
void write(int x) { if(x>=10) write(x/10); putchar('0'+x%10); }
const int mod = 998244353;
int qpo(int a,int b) {int res=1; for(;b;b>>=1,a=(a*a)%mod) if(b&1) res=res*a%mod; return res; }
int inv(int a) {return qpo(a,mod-2); }
#define maxn 200050
int n,a[maxn];
void work() {
in1(n);
For(i,1,n) in1(a[i]);
a[n+1]=0;
int ans=0;
int i=2;
while(i<=n) {
int res=a[i-1]+a[i+1]-a[i];
if(res>0) {
ans+=res;
a[i+1]-=min(a[i+1],res);
res-=min(a[i+1],res);
a[i]-=res;
}
i+=2;
}
cout<<ans<<'\n';
}
signed main() {
// freopen("data.in","r",stdin);
// freopen("myans.out","w",stdout);
// ios::sync_with_stdio(false);
// cin.tie(0); cout.tie(0);
double stt=clock();
int _=1;
_=read();
// cin>>_;
For(i,1,_) {
work();
}
cerr<<"\nTotal Time is:"<<(clock()-stt)*1.0/1000<<" second(s)."<<'\n';
return 0;
}
D
题目大意
给定一棵有 \(n\) 个顶点的树,顶点编号从 \(1\) 到 \(n\)。可以通过滑动操作修改树的结构:选择三个不同的顶点 \(a\), \(b\), 和 \(c\),其中 \(b\) 与 \(a\) 和 \(c\) 都直接相连;然后对于 \(b\) 的每个邻居 \(d\)(除了 \(a\) 和 \(c\)),移除 \(b\) 和 \(d\) 之间的边,并将 \(d\) 直接连接到 \(c\)。操作后树仍保持为树。目标是通过一系列滑动操作将树转换为路径图(每个顶点度数不超过 \(2\)),并最小化操作次数。只需输出最优操作序列中的第一个操作(如果至少需要一次操作)。
大致思路
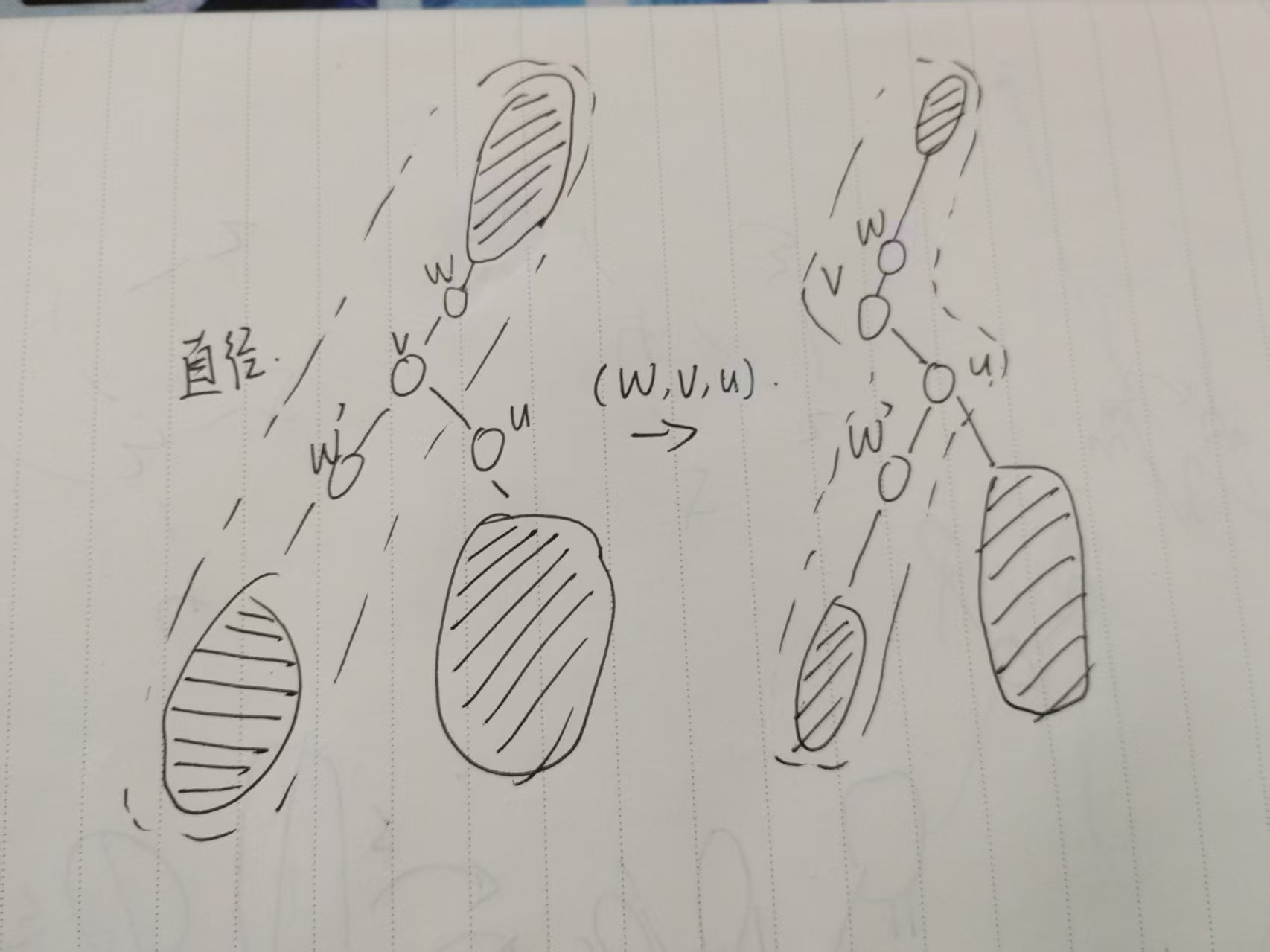
注意到每次对树的直径的移动最多使直径增加 \(1\),我们只需要每次都使直径增加即可。找出树的直径,对于一个不在直径上且与直径链接的点 \(u\),设该点与直径相连的直径上的点为 \(v\),直径上任意的与 \(v\) 直接相连的的一点 \(w\),那么可以通过构造一个 \((w,v,u)\) 使得另一个直径上与 \(v\) 直接相连的点从连到 \(v\) 变成连到 \(u\)。
代码
https://codeforces.com/contest/2134/submission/335737063
点击查看代码
#include<bits/stdc++.h>
#define pii pair<int,int>
#define pll pair<long long,long long>
#define ll long long
#define i128 __int128
#define mem(a,b) memset((a),(b),sizeof(a))
#define m0(a) memset((a),0,sizeof(a))
#define m1(a) memset(a,-1,sizeof(a))
#define lb(x) ((x)&-(x))
#define lc(x) ((x)<<1)
#define rc(x) (((x)<<1)|1)
#define pb(G,x) (G).push_back((x))
#define For(a,b,c) for(int a=(b);a<=(c);a++)
#define Rep(a,b,c) for(int a=(b);a>=(c);a--)
#define in1(a) a=read()
#define in2(a,b) a=read(), b=read()
#define in3(a,b,c) a=read(), b=read(), c=read()
#define in4(a,b,c,d) a=read(), b=read(), c=read(), d=read()
#define fst first
#define scd second
#define dbg puts("IAKIOI")
using namespace std;
int read() {
int x=0,f=1; char c=getchar();
for(;c<'0'||c>'9';c=getchar()) f=(c=='-'?-1:1);
for(;c<='9'&&c>='0';c=getchar()) x=(x<<1)+(x<<3)+(c^48);
return x*f;
}
void write(int x) { if(x>=10) write(x/10); putchar('0'+x%10); }
const int mod = 998244353;
int qpo(int a,int b) {int res=1; for(;b;b>>=1,a=(a*a)%mod) if(b&1) res=res*a%mod; return res; }
int inv(int a) {return qpo(a,mod-2); }
#define maxn 200050
int n;
vector<int> G[maxn];
int dep[maxn],f[maxn];
void dfs(int u,int fa) {
dep[u]=dep[fa]+1; f[u]=fa;
for(auto v:G[u]) if(v!=fa) dfs(v,u);
}
void work() {
in1(n);
For(i,2,n) {
int u,v; in2(u,v);
G[u].push_back(v),G[v].push_back(u);
}
dep[1]=0; dfs(1,1);
int mx=1; For(i,2,n) if(dep[mx]<dep[i]) mx=i;
dep[mx]=0; dfs(mx,mx);
int qwq=1; For(i,2,n) if(dep[qwq]<dep[i]) qwq=i;
bool flg=0;
while(qwq!=mx) {
if(G[f[qwq]].size()>2) {
cout<<qwq<<' '<<f[qwq]<<' ';
for(auto v:G[f[qwq]]) if(v!=qwq&&v!=f[f[qwq]]) {
cout<<v<<'\n'; flg=1;
break ;
}
}
qwq=f[qwq];
if(flg) break;
}
if(!flg) cout<<-1<<'\n';
For(i,1,n) G[i].clear();
}
signed main() {
// freopen("data.in","r",stdin);
// freopen("myans.out","w",stdout);
// ios::sync_with_stdio(false);
// cin.tie(0); cout.tie(0);
double stt=clock();
int _=1;
_=read();
// cin>>_;
For(i,1,_) {
work();
}
cerr<<"\nTotal Time is:"<<(clock()-stt)*1.0/1000<<" second(s)."<<'\n';
return 0;
}
本文来自博客园,作者:coding_goat_qwq,转载请注明原文链接:https://www.cnblogs.com/CodingGoat/p/19060295


 浙公网安备 33010602011771号
浙公网安备 33010602011771号