[CSP-S2019] 括号树

题目背景

本题中合法括号串的定义如下：

1. () 是合法括号串。
2. 如果 A 是合法括号串，则 (A) 是合法括号串。
3. 如果 A，B 是合法括号串，则 AB 是合法括号串。

本题中子串与不同的子串的定义如下：

1. 字符串 S 的子串是 S 中连续的任意个字符组成的字符串。S 的子串可用起始位置 \(l\) 与终止位置 \(r\) 来表示，记为 \(S (l, r)\)（\(1 \leq l \leq r \leq |S |\)，\(|S |\) 表示 S 的长度）。
2. S 的两个子串视作不同当且仅当它们在 S 中的位置不同，即 \(l\) 不同或 \(r\) 不同。

题目描述

一个大小为 \(n\) 的树包含 \(n\) 个结点和 \(n − 1\) 条边，每条边连接两个结点，且任意两个结点间有且仅有一条简单路径互相可达。

小 Q 是一个充满好奇心的小朋友，有一天他在上学的路上碰见了一个大小为 \(n\) 的树，树上结点从 \(1\) ∼ \(n\) 编号，\(1\) 号结点为树的根。除 \(1\) 号结点外，每个结点有一个父亲结点，\(u\)（\(2 \leq u \leq n\)）号结点的父亲为 \(f_u\)（\(1 ≤ f_u < u\)）号结点。

小 Q 发现这个树的每个结点上恰有一个括号，可能是( 或)。小 Q 定义 \(s_i\) 为：将根结点到 \(i\) 号结点的简单路径上的括号，按结点经过顺序依次排列组成的字符串。

显然 \(s_i\) 是个括号串，但不一定是合法括号串，因此现在小 Q 想对所有的 \(i\)（\(1\leq i\leq n\)）求出，\(s_i\) 中有多少个互不相同的子串是合法括号串。

这个问题难倒了小 Q，他只好向你求助。设 \(s_i\) 共有 \(k_i\) 个不同子串是合法括号串， 你只需要告诉小 Q 所有 \(i \times k_i\) 的异或和，即：

\[(1 \times k_1)\ \text{xor}\ (2 \times k_2)\ \text{xor}\ (3 \times k_3)\ \text{xor}\ \cdots\ \text{xor}\ (n \times k_n) \]

其中 \(xor\) 是位异或运算。

输入格式

第一行一个整数 \(n\)，表示树的大小。

第二行一个长为 \(n\) 的由( 与) 组成的括号串，第 \(i\) 个括号表示 \(i\) 号结点上的括号。

第三行包含 \(n − 1\) 个整数，第 \(i\)（\(1 \leq i \lt n\)）个整数表示 \(i + 1\) 号结点的父亲编号 \(f_{i+1}\)。

输出格式

仅一行一个整数表示答案。

样例 #1

样例输入 #1

5
(()()
1 1 2 2

样例输出 #1

6

提示

【样例解释1】

树的形态如下图：

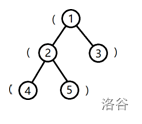
将根到 1 号结点的简单路径上的括号，按经过顺序排列所组成的字符串为 (，子串是合法括号串的个数为 \(0\)。

将根到 2 号结点的字符串为 ((，子串是合法括号串的个数为 \(0\)。

将根到 3 号结点的字符串为 ()，子串是合法括号串的个数为 \(1\)。

将根到 4 号结点的字符串为 (((，子串是合法括号串的个数为 \(0\)。

将根到 5 号结点的字符串为 (()，子串是合法括号串的个数为 \(1\)。

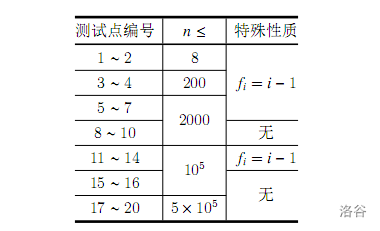
【数据范围】

Solution：

一个合法括号序列：

	(1) 左右括号数量相同(最终栈为空)

	(2) 对于任意一个前缀，左括号数 >= 右括号数 

对于每一个节点，所有新增括号序列一定以当前节点为右端点

设: 从根节点到当前节点\(u\)所构成括号序列中，合法括号子串的数量为\(F(u)\)

以\(u\)为右端点的合法括号序列数量为\(W(u)\)，则：

\(W(u)=W(stack.top()-1)+1\)

\(F(u)=F(Fa_u)+W(u)\)

在树上维护一个栈：

若当前括号为(，将当前接点入栈

若当前括号为)，如果栈不空，将当前括号与栈顶(匹配

注意回溯

Code:

#include <cstdio>
#include <cstring>

typedef long long ll;

const int N=5e5+5;

int n;
int idx,h[N],p[N];
int top,stk[N];
ll f[N],g[N];
char s[N];
struct node
{
    int nxt,to;
}e[N];

void add(int nxt,int to)
{
    e[++idx].nxt=h[nxt];
    e[idx].to=to;
    h[nxt]=idx;
}
void dfs(int u)
{
    if(s[u]=='(')
    {
        stk[++top]=u;
        f[u]=f[p[u]];
        for(int i=h[u];~i;i=e[i].nxt)dfs(e[i].to);
        --top;
    }
    else
    {
        if(!top)
        {
            f[u]=f[p[u]];
            for(int i=h[u];~i;i=e[i].nxt)dfs(e[i].to);
        }
        else
        {
            int t=stk[top--];
            g[u]=g[p[t]]+1;
            f[u]=f[p[u]]+g[u];
            for(int i=h[u];~i;i=e[i].nxt)dfs(e[i].to);
            stk[++top]=t;
        }
    }
}
int main()
{
    scanf("%d",&n);
    scanf("%s",s+1);

    memset(h,-1,sizeof(h));
    for(int i=2;i<=n;++i)
    {
        scanf("%d",&p[i]);
        add(p[i],i);
    }

    dfs(1);

    ll res=0;
    for(int i=1;i<=n;++i)res^=i*f[i];
    printf("%lld\n",res);
    return 0;
}