[NOIP2015 提高组] 信息传递

题目描述

有 \(n\) 个同学（编号为 \(1\) 到 \(n\) ）正在玩一个信息传递的游戏。在游戏里每人都有一个固定的信息传递对象，其中，编号为 \(i\) 的同学的信息传递对象是编号为 \(T_i\) 的同学。

游戏开始时，每人都只知道自己的生日。之后每一轮中，所有人会同时将自己当前所知的生日信息告诉各自的信息传递对象（注意：可能有人可以从若干人那里获取信息， 但是每人只会把信息告诉一个人，即自己的信息传递对象）。当有人从别人口中得知自 己的生日时，游戏结束。请问该游戏一共可以进行几轮？

输入格式

共\(2\)行。

第\(1\)行包含1个正整数 \(n\) ，表示 \(n\) 个人。

第\(2\)行包含 \(n\) 个用空格隔开的正整数 \(T_1,T_2,\cdots\cdots,T_n\) ，其中第 \(i\) 个整数 \(T_i\) 表示编号为 \(i\) 的同学的信息传递对象是编号为 \(T_i\) 的同学， \(T_i \leq n\) 且 \(T_i \neq i\) 。

输出格式

\(1\)个整数，表示游戏一共可以进行多少轮。

样例输入

5
2 4 2 3 1

样例输出

3

提示

样例1解释

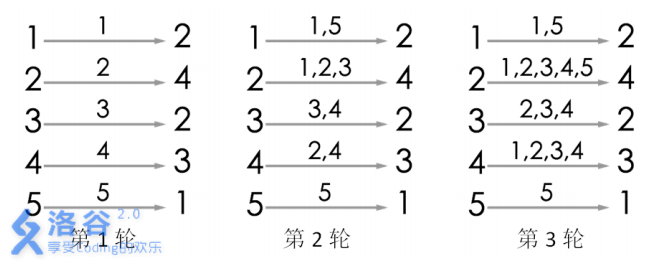
游戏的流程如图所示。当进行完第$ 3$ 轮游戏后， $4 $号玩家会听到 \(2\) 号玩家告诉他自己的生日，所以答案为 \(3\)。当然，第 \(3\) 轮游戏后，$ 2 $号玩家、 \(3\) 号玩家都能从自己的消息来源得知自己的生日，同样符合游戏结束的条件。

对于 \(30\%\)的数据， \(n ≤ 200\)；

对于 \(60\%\)的数据， \(n ≤ 2500\)；

对于$ 100%$的数据， \(n ≤ 200000\)。

Solution:

基环树求最小环

Code

#1 拓扑排序保留环上点+DFS

#include <cstdio>
#include <algorithm>
#include <queue>
#include <cstring>

using namespace std;

const int N=2e5+5;

int n,idx,cnt;
int a[N],din[N],h[N];
bool st[N];
struct node
{
    int nxt,to;
}e[N];

void add(int nxt,int to)
{
    e[++idx].nxt=h[nxt];
    e[idx].to=to;
    h[nxt]=idx;
}
void dfs(int u)
{
    if(st[u])return;
    ++cnt;
    st[u]=1;
    for(int i=h[u];~i;i=e[i].nxt)
    {
        int v=e[i].to;
        dfs(v);
    }
}
int main()
{
    scanf("%d",&n);

    memset(h,-1,sizeof(h));
    for(int i=1;i<=n;++i)
    {
        scanf("%d",&a[i]);
        add(i,a[i]);
        din[a[i]]++;
    }
    
    queue<int> q;
    for(int i=1;i<=n;++i)
        if(!din[i])
            q.push(i);
    while(q.size())
    {
        int u=q.front();
        q.pop();
        st[u]=1;
        for(int i=h[u];~i;i=e[i].nxt)
        {
            int v=e[i].to;
            if(--din[v]==0)q.push(v);
        }
    }

    memset(h,-1,sizeof(h));
    idx=0;
    for(int i=1;i<=n;++i)
        if(!st[i])
            add(i,a[i]);

    int ans=N;
    for(int i=1;i<=n;++i)
        if(!st[i])
        {
            cnt=0;
            dfs(i);
            ans=min(ans,cnt);
        }

    printf("%d\n",ans);
    return 0;
}

#2 栈:无论从那个点开始,都会走到环上

#include <cstdio>
#include <algorithm>
#include <queue>
#include <cstring>

using namespace std;

const int N=2e5+5;

int n,ans=N;
int a[N],stk[N];
bool st[N],in_stk[N];

int main()
{
    scanf("%d",&n);

    for(int i=1;i<=n;++i)
        scanf("%d",&a[i]);

    for(int i=1;i<=n;++i)
        if(!st[i])
        {
            int j=i,top=0;
            while(!st[j])
            {
                stk[++top]=j;
                in_stk[j]=1;
                st[j]=1;
                j=a[j];
            }
            if(in_stk[j])
            {
                int cnt=1;
                while(stk[top]!=j)
                {
                    ++cnt;
                    in_stk[stk[top--]]=0;
                }
                ans=min(ans,cnt);
            }
            while(top)in_stk[stk[top--]]=0;
        }
    printf("%d\n",ans);

    return 0;
}