【C语言数据结构与算法】四、线性表之双链表
双链表
观看这里的uu建议先看单链表
线性表之单链表点击这里
一、前言
线性表(linear list)是n个具有相同特性的数据元素的有限序列。 线性表是一种在实际中广泛使用的数据结构,常见的线性表:顺序表、链表、栈、队列等。
线性表在逻辑上是线性结构,也就说是连续的一条直线。但是在物理结构上并不一定是连续的,线性表在物理上存储时,通常以数组和链式结构的形式存储。
链表是典型的线性表之一,以链式结构的形式存储。
链表又被分为单链表和双链表。
本片仅对双链表详细说明。
二、双链表
1·双链表的概念及其结构
概念:双链表是一种物理存储结构上非连续、非顺序的存储结构,数据元素的逻辑顺序是通过链表中的指针双向链接次序实现的。
逻辑结构图如下:

根据双链表的逻辑结构可以想到双链表这种结构体中包含存入的数据、指向下一个结构体的结构体指针和指向上一个结构体的结构体指针。
双链表最大的优势就是双链表结构体的成员变量中包含上一个节点的地址,这样操作起来非常方便并且不需要遍历找上一节点的地址,基本没有效率损失,完美解决了单链表存在缺点。
2·双链表的分类
实际中要实现的双链表的结构非常多样,以下是两种双链表结构:
- 不带头非循环双链表
![在这里插入图片描述]()
- 带头循环双链表
![在这里插入图片描述]()
实际中最常用的是带头循环双链表。
带头循环双链表:结构最复杂,一般用在单独存储数据。实际中使用的链表数据结构,都是带头双向循环链表。另外这个结构虽然结构复杂,但是使用代码实现以后会发现结构会带来很多优势,实现反而简单了。
双链表是否带头的区别:当不带头要改变头指针的指向时,那么就需要传二级指针形参来改变头指针的指向;当带头时只需要传一级指针,操作头节点来处理后续数据的操作即可。
双链表是否循环的区别:当非循环时进行尾部操作时,头节点与尾节点没有逻辑上的联系,尾部操作不是很方便;当循环时进行尾部操作时,头节点与尾节点有逻辑上的联系,使用起来方便许多。
说明:
双链表无论带头或不带头、循环或非循环的实现都大同小异,这里只详细说明带头+循环双链表的实现。
3·双链表的接口函数
双链表头文件List.h的声明如下:
#pragma once
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
//带头+双向+循环链表增删查改实现
typedef int LTDataType;
//带头+循环双向链表结构体
typedef struct ListNode
{
//存储的数据
LTDataType data;
//指向下一节点的结构体指针
struct ListNode* next;
//指向上一节点的结构体指针
struct ListNode* prev;
}LTNode;
// 创建返回链表的头结点.
LTNode* ListCreate();
// 动态申请一个节点
LTNode* BuyListNode(LTDataType x);
// 双向链表销毁
void ListDestory(LTNode* plist);
// 双向链表打印
void ListPrint(LTNode* plist);
// 双向链表尾插
void ListPushBack(LTNode* plist, LTDataType x);
// 双向链表尾删
void ListPopBack(LTNode* plist);
// 双向链表头插
void ListPushFront(LTNode* plist, LTDataType x);
// 双向链表头删
void ListPopFront(LTNode* plist);
// 双向链表查找
ListNode* ListFind(LTNode* plist, LTDataType x);
// 双向链表在pos的前面进行插入
void ListInsert(LTNode* pos, LTDataType x);
// 双向链表删除pos位置的节点
void ListErase(LTNode* pos);
三、双链表的实现
说明:以下函数的实现思路在代码注释中已详细解释。
1·申请头节点、申请新节点、打印链表和释放链表
申请头节点函数在List.c中如下:
// 创建返回链表的头结点.
LTNode* ListCreate()
{
LTNode* phead = (LTNode*)malloc(sizeof(LTNode));
//开辟失败则报错且终止程序
if (phead == NULL)
{
printf("malloc fail");
exit(-1);
}
else
{
//头节点的下一节点和上一节点都指向自己,存入数据为随机值
phead->next = phead;
phead->prev = phead;
//返回头节点
return phead;
}
}
申请新节点函数在List.c中如下:
// 动态申请一个节点
LTNode* BuyListNode(LTDataType x)
{
LTNode* newnode = (LTNode*)malloc(sizeof(LTNode));
//开辟失败则报错且终止程序
if (newnode == NULL)
{
printf("malloc fail");
exit(-1);
}
else
{
newnode->data = x;
return newnode;
}
}
说明:申请头节点只要使用带头循环双向链表都会用到,申请新节点只要插入节点都会用到,因此申请新节点在尾部插入节点、头部插入节点和任意位置插入节点据函数中嵌套使用。
打印链表函数在List.c中如下:
// 双向链表打印
void ListPrint(LTNode* phead)
{
//遍历链表从头节点后一节点出发
LTNode* cur = phead->next;
//当指向头节点时结束遍历,无空指针
while (cur != phead)
{
printf("%d ", cur->data);
//移动指针
cur = cur->next;
}
}
释放链表函数在List.c中如下:
// 双向链表销毁
void ListDestory(LTNode* phead)
{
LTNode* cur = phead->next;
//遍历链表
while (cur != phead)
{
//保存当前节点的下一节点,因为马上要释放当前节点
LTNode* next = cur->next;
free(cur);
cur = NULL;
//移动当前节点
cur = next;
}
//释放头节点
free(phead);
phead = NULL;
}
以上函数的具体实现情况尾部、头部和任意位置操作时大同小异且比较简单,不做具体说明,看注释即可。
2·尾部插入节点&尾部删除节点
尾部插入节点函数在List.c中如下:
// 双向链表尾插
//由于空链表有一个头节点,因此在空链表插入数据时也适用
void ListPushBack(LTNode* phead, LTDataType x)
{
//申请新节点
LTNode* newnode = BuyListNode(x);
//因为循环所以头节点的上一节点为尾节点
LTNode* tail = phead->prev;
//1·此时newnode为新尾节点,所以phead的上一节点变为新尾节点
phead->prev = newnode;
//2·因为循环,所以新尾节点的下一节点为头节点
newnode->next = phead;
//3·新尾节点的上一节点为之前的尾节点
newnode->prev = tail;
//4·之前尾节点的下一节点为新尾节点
tail->next = newnode;
}
时间复杂度为O(1),基本不损失效率。
尾部删除节点函数在List.c中如下:
// 双向链表尾删
void ListPopBack(LTNode* phead)
{
//链表只剩头节点时为空链表,不可再尾删
assert(phead->next != phead);
//保存旧尾节点
LTNode* tail = phead->prev;
//1·头节点的prev变为旧尾节点的prev,
phead->prev = tail->prev;
//2·新尾节点(旧尾节点的上一节点)的下一节点变为头节点
tail->prev->next = phead;
//3·释放旧尾节点
free(tail);
tail = NULL;
}
时间复杂度为O(1),基本不损失效率。
具体使用方式如下:
#include <iostream>
#include "List.h"
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
//尾删尾插
void ListTest1()
{
LTNode* plist = ListCreate();
//尾插数据
ListPushBack(plist, 1);
ListPushBack(plist, 2);
ListPushBack(plist, 3);
ListPushBack(plist, 4);
//打印插入后数据
ListPrint(plist);
printf("\n");
//尾删数据
ListPopBack(plist);
ListPopBack(plist);
ListPopBack(plist);
//打印删除后数据
ListPrint(plist);
printf("\n");
//继续删除两个数据,会报错
ListPopBack(plist);
ListPopBack(plist);
}
int main()
{
ListTest1();
return 0;
}
执行调试结果如下:
1·向尾部添加4个节点,并对相应变量进行监测:
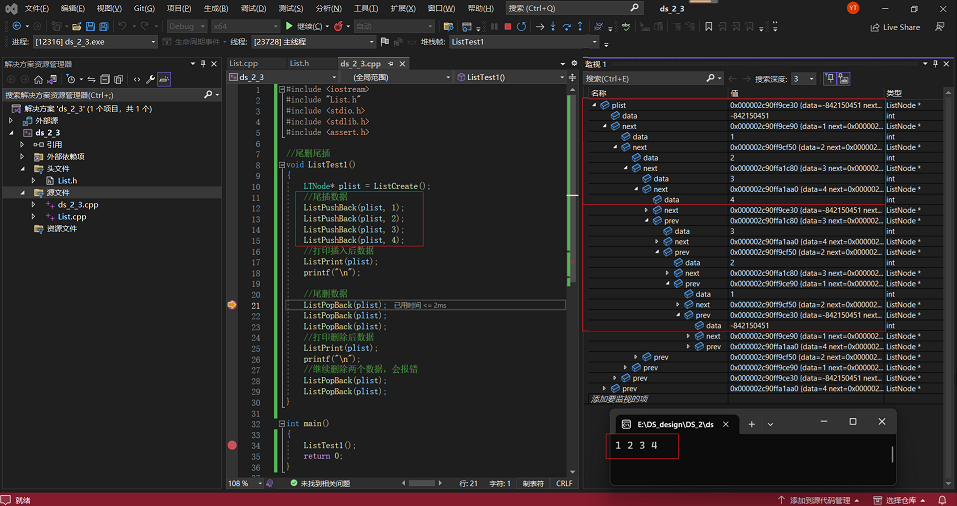
2·以上面情况为基础,从尾部删除3个节点,并对相应变量进行监测:
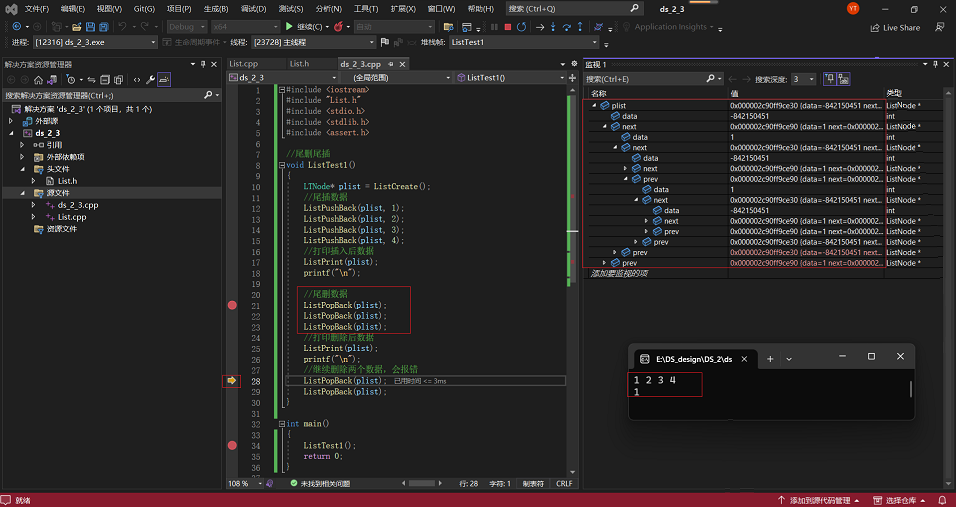
3·以上面情况为基础,再从尾部删除2个节点,并对相应变量进行监测:
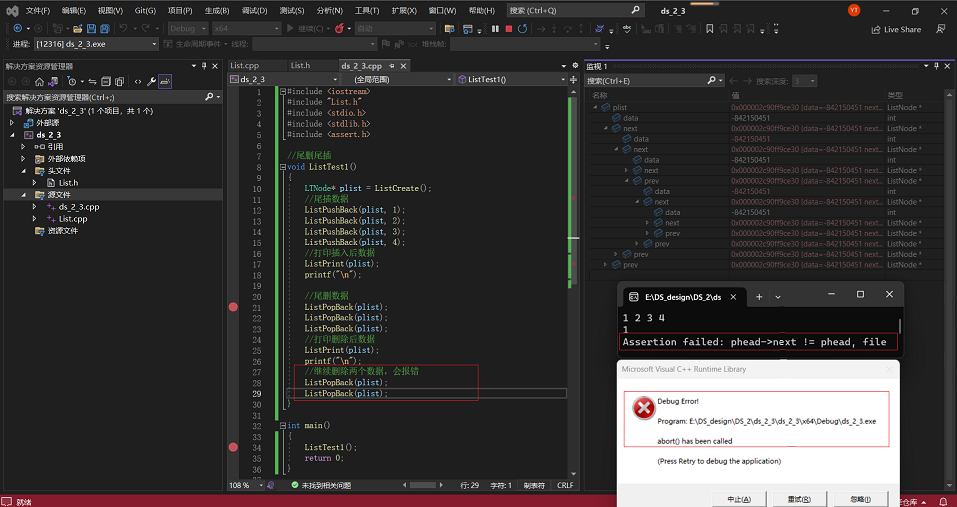
3·头部插入节点&头部删除节点
头部插入节点函数在List.c中如下:
// 双向链表头插
//链表空或非空都适用
void ListPushFront(LTNode* phead, LTDataType x)
{
//申请新节点
LTNode* newnode = BuyListNode(x);
//1·新节点的next变为头节点的下一节点
newnode->next = phead->next;
//2·头节点的下节点的prev变为新节点
phead->next->prev = newnode;
//3·新节点的prev变为头节点
newnode->prev = phead;
//4·头节点的下一节点为新节点
phead->next = newnode;
}
时间复杂度为O(1),基本不损失效率。
头部删除节点函数在List.c中如下:
// 双向链表头删
void ListPopFront(LTNode* phead)
{
//空链表禁止删除
assert(phead->next != phead);
//保存首节点
LTNode* strt = phead->next;
//1·头节点的next变为首节点的下一个节点
phead->next = strt->next;
//2·首节点的下一节点的prev变为头节点
strt->next->prev = phead;
//释放首字节
free(strt);
strt = NULL;
}
时间复杂度为O(1),基本不损失效率。
具体使用方式如下:
#include <iostream>
#include "List.h"
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
//头删头插
void ListTest2()
{
LTNode* plist = ListCreate();
//头插数据
ListPushFront(plist, 1);
ListPushFront(plist, 2);
ListPushFront(plist, 3);
ListPushFront(plist, 4);
//打印插入后数据
ListPrint(plist);
printf("\n");
//头删数据
ListPopFront(plist);
ListPopFront(plist);
ListPopFront(plist);
//打印删除后数据
ListPrint(plist);
printf("\n");
//继续删除两个数据,会报错
ListPopFront(plist);
ListPopFront(plist);
}
int main()
{
ListTest2();
return 0;
}
执行调试结果如下:
1·向头部添加4个节点,并对相应变量进行监测:
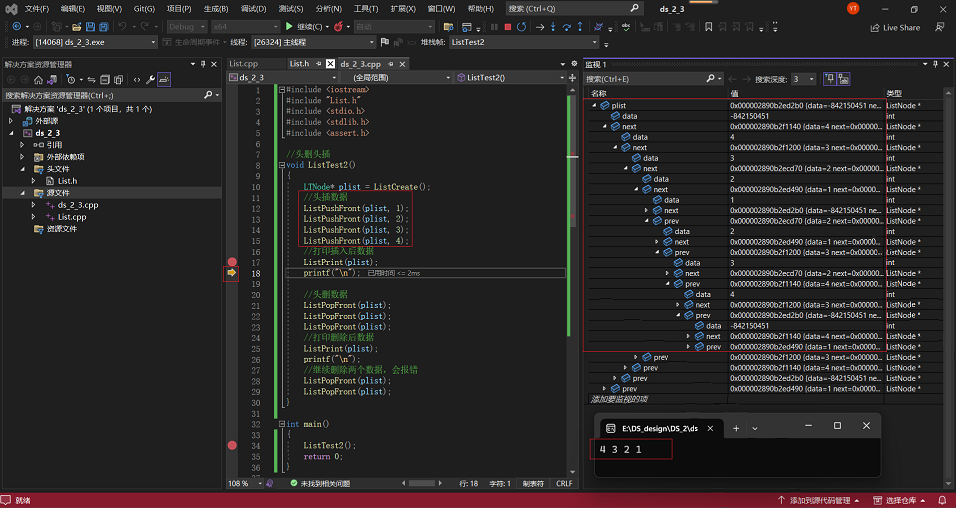
2·以上面情况为基础,从头部删除3个节点,并对相应变量进行监测:
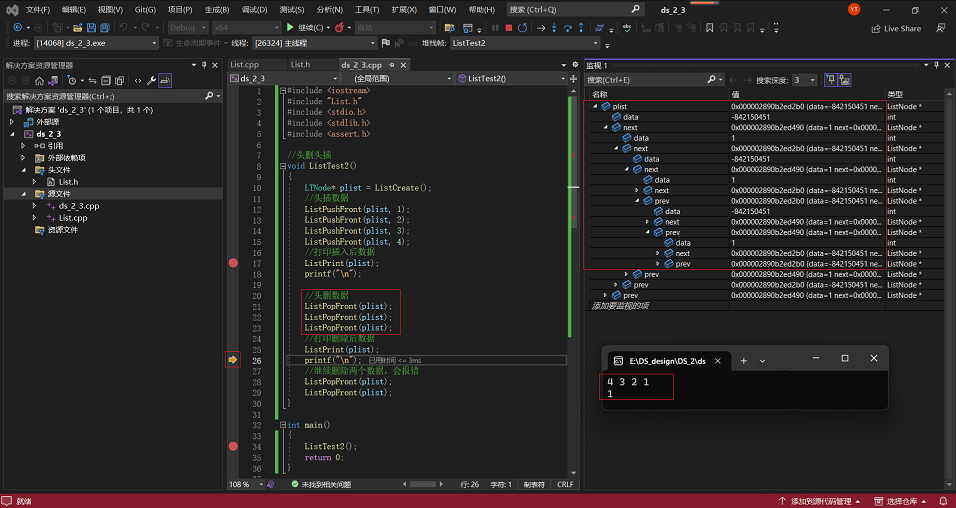
3·以上面情况为基础,再从头部删除2个节点,并对相应变量进行监测:
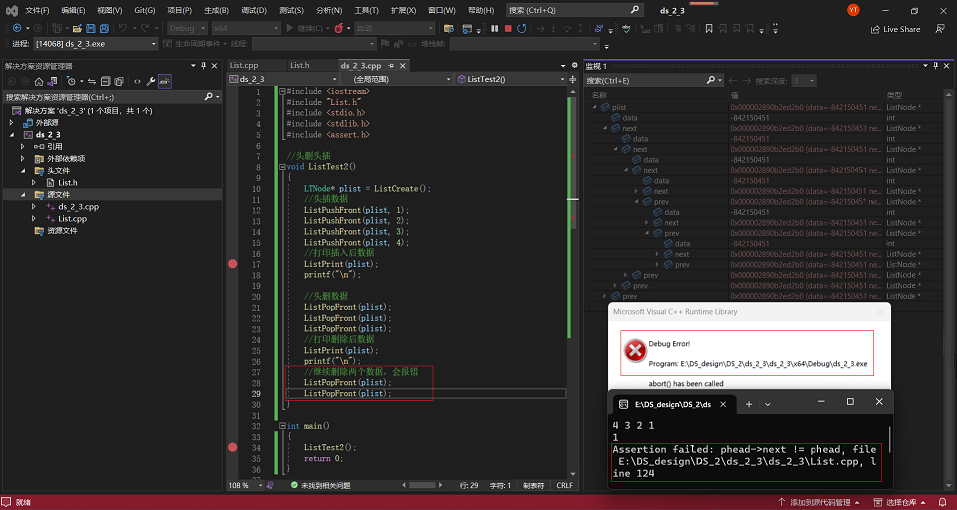
4·查找节点
查找函数在List.c中如下:
// 双向链表查找
LTNode* ListFind(LTNode* phead, LTDataType x)
{
//保存首节点
LTNode* cur = phead->next;
//遍历链表
while (cur != phead)
{
//找到返回当前指针
if (cur->data == x)
{
return cur;
}
//遍历时未找到,移动指针
cur = cur->next;
}
//遍历结束未找到,返回空指针
return NULL;
}
具体使用方式如下:
#include <iostream>
#include "List.h"
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
//查找
void ListTest3()
{
LTNode* plist = ListCreate();
//尾插数据
ListPushBack(plist, 1);
ListPushBack(plist, 2);
ListPushBack(plist, 3);
ListPushBack(plist, 4);
//打印插入后数据
ListPrint(plist);
printf("\n");
//查找3并打印
LTNode* pos = ListFind(plist, 3);
if (pos != NULL)
{
printf("找到数据:%d", pos->data);
}
}
int main()
{
ListTest3();
return 0;
}
执行调试结果如下:
在尾插数据1234情况下,查找数据3,并对相应变量进行监测:
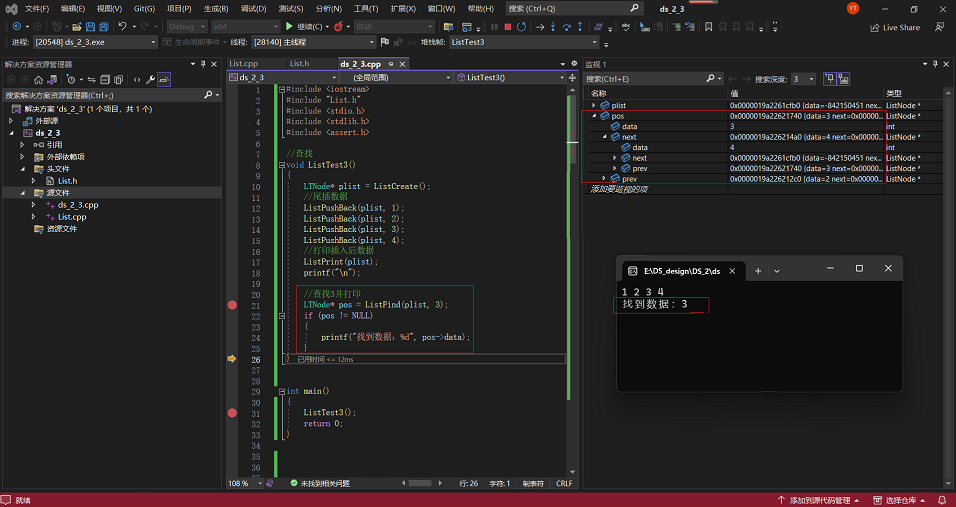
5·任意位置插入节点&任意位置删除节点
说明:这组函数常与查找函数配合使用,即先找到对应数据,然后在对应数据周围或数据本身处进行操作。
任意位置插入节点函数在List.c中如下:
// 双向链表在pos处进行插入
//在头节点phead处插入就是尾插,因为循环
//在phead->next插入就是头插
void ListInsert(LTNode* pos, LTDataType x)
{
//申请新节点
LTNode* newnode = BuyListNode(x);
//1·将新节点的next改为当前节点
newnode->next = pos;
//2·将当前节点的上一节点的next改为新节点
pos->prev->next = newnode;
//3·将新节点的prev改为当前节点的上一节点
newnode->prev = pos->prev;
//4·将当前节点的prev改为新节点
pos->prev = newnode;
}
时间复杂度为O(1),基本不损失效率。
任意位置删除节点函数在List.c中如下:
// 双向链表删除pos位置的节点
//删除phead->next就是头删
//删除phead->prev就是尾删
void ListErase(LTNode* pos)
{
//禁止删除头节点
assert(pos->next != pos);
//1·当前位置的上一节点的next变为当前节点的下一节点
pos->prev->next = pos->next;
//2·当前位置的下一节点的prev变为当前节点的上一节点
pos->next->prev = pos->prev;
//释放当前位置的节点
free(pos);
pos = NULL;
}
时间复杂度为O(1),基本不损失效率。
具体使用方式如下:
#include <iostream>
#include "List.h"
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
//任意位置删除任意位置插入
void ListTest4()
{
LTNode* plist = ListCreate();
//尾插数据
ListPushBack(plist, 1);
ListPushBack(plist, 2);
ListPushBack(plist, 3);
//打印插入后数据
ListPrint(plist);
printf("\n");
//在2处插入数据4
LTNode* pos1 = ListFind(plist, 2);
if (pos1 != NULL)
{
ListInsert(pos1, 4);
}
//打印插入后数据
ListPrint(plist);
printf("\n");
//尾插5
LTNode* pos2 = ListFind(plist, 1);
if (pos2 != NULL)
{
ListInsert(pos2->prev, 5);
}
//打印插入后数据
ListPrint(plist);
printf("\n");
//头插6
LTNode* pos3 = ListFind(plist, 1);
if (pos3 != NULL)
{
ListInsert(pos3, 6);
}
//打印插入后数据
ListPrint(plist);
printf("\n");
//614235
//删除1
LTNode* pos4 = ListFind(plist, 1);
if (pos4 != NULL)
{
ListErase(pos4);
}
//打印删除后数据
ListPrint(plist);
printf("\n");
//头删6
LTNode* pos5 = ListFind(plist, 6);
if (pos5 != NULL)
{
ListErase(pos5);
}
//打印删除后数据
ListPrint(plist);
printf("\n");
//尾删5
LTNode* pos6 = ListFind(plist, 5);
if (pos6 != NULL)
{
ListErase(pos6);
}
//打印删除后数据
ListPrint(plist);
printf("\n");
}
int main()
{
ListTest4();
return 0;
}
执行调试结果如下:
1·在已有123数据情况下,在2处插入4,并对相应变量进行监测:
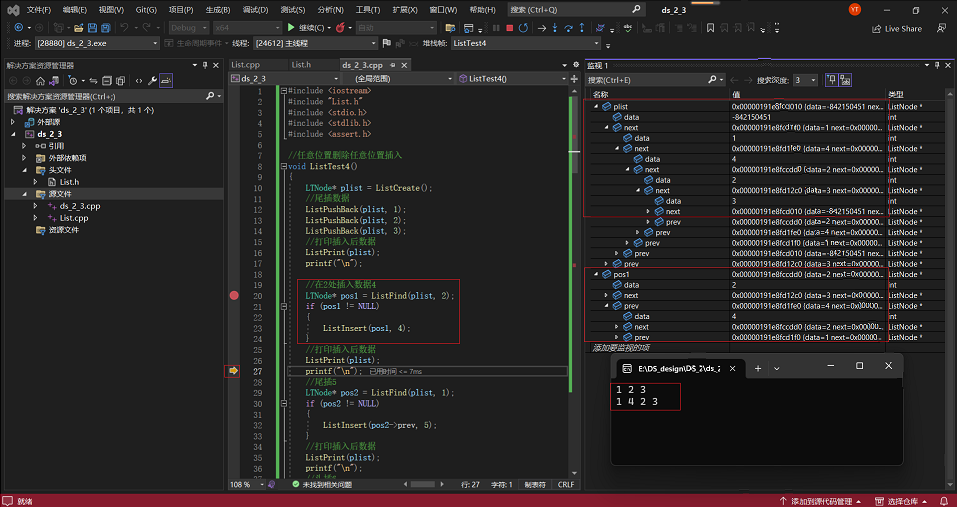
2·以上面情况为基础,再从尾部插入5,并对相应变量进行监测:
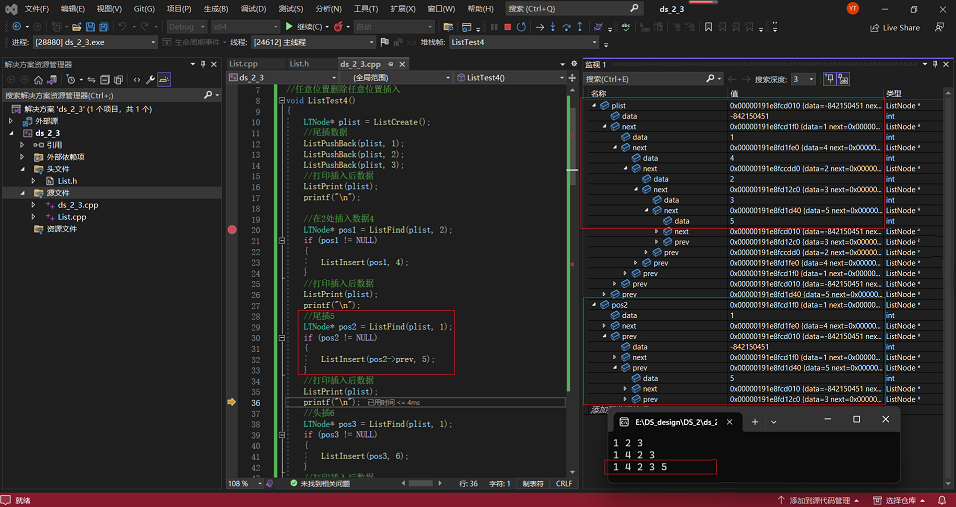
3·以上面情况为基础,再从头部插入6,并对相应变量进行监测:
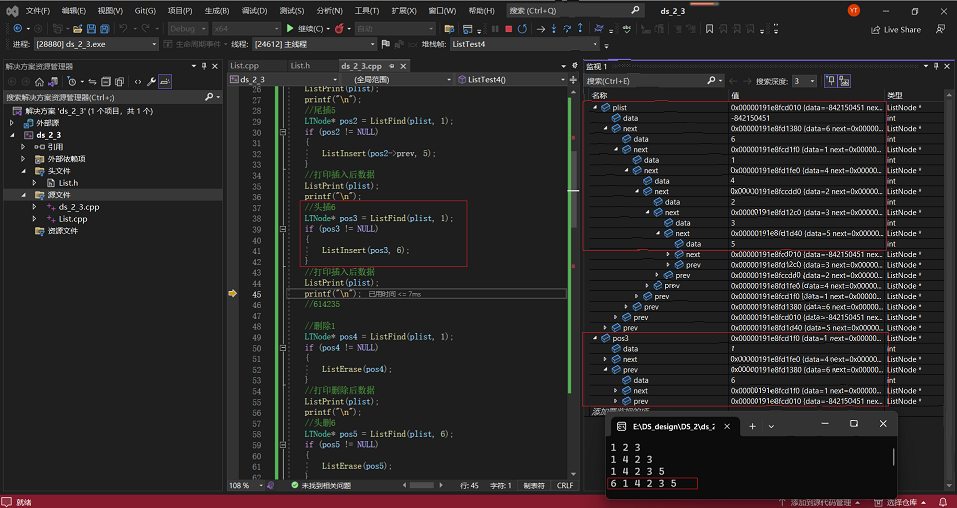
4·以上面情况为基础,删除1,并对相应变量进行监测:
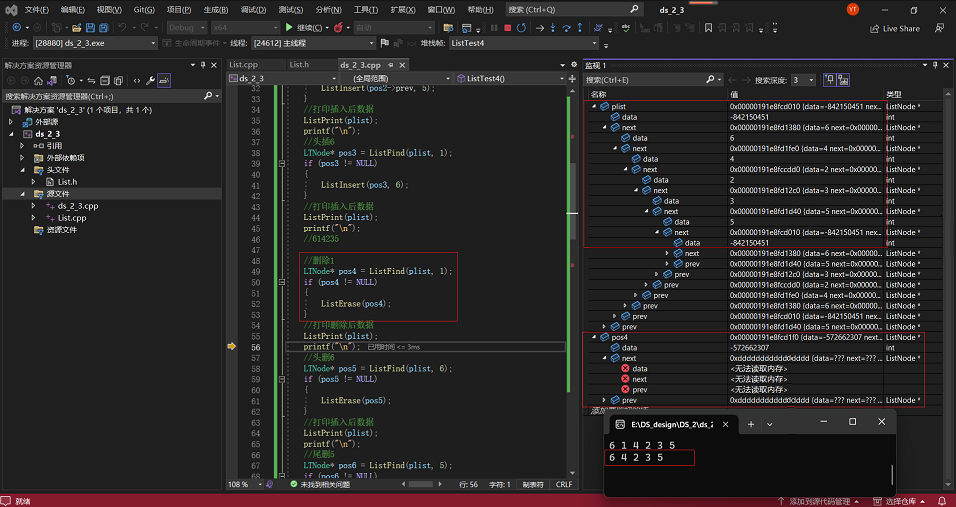
5·以上面情况为基础,删除头部6,并对相应变量进行监测:
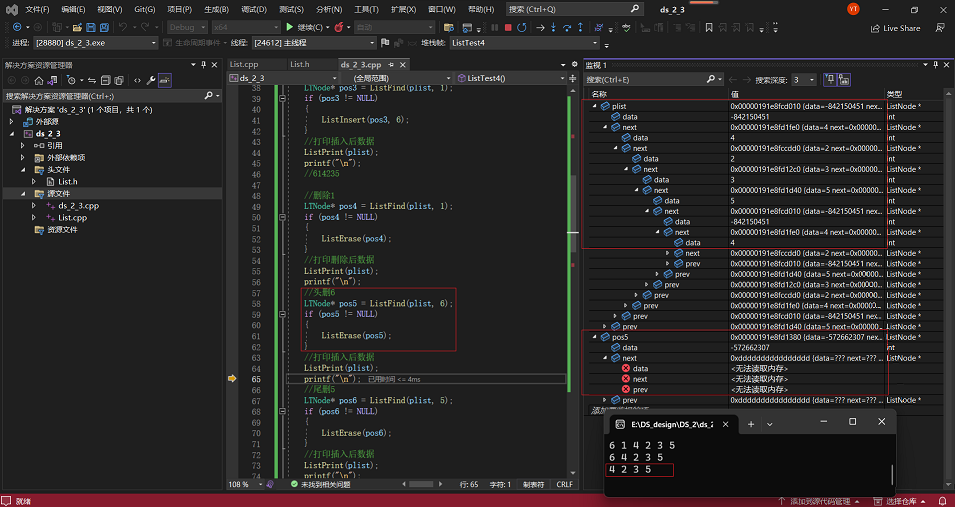
6·以上面情况为基础,删除尾部5,并对相应变量进行监测:
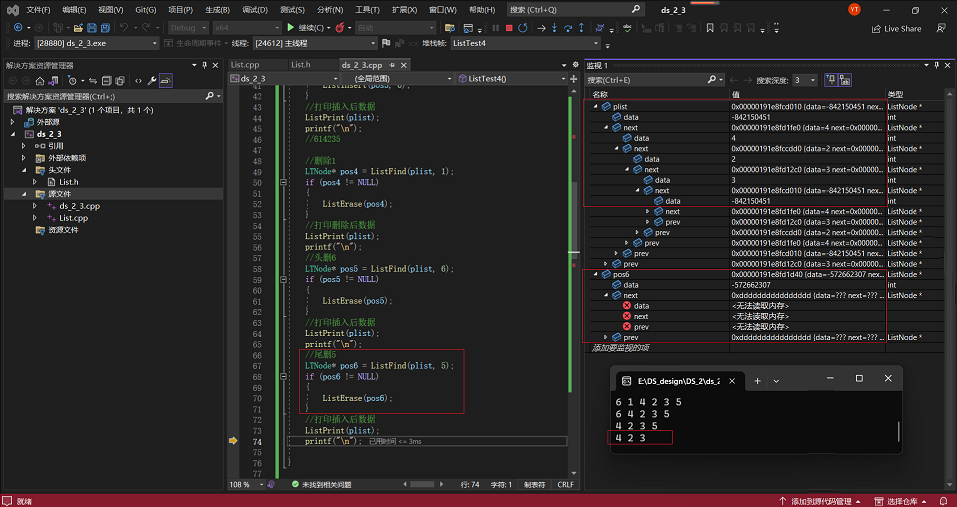
四、双链表的缺点
双链表相比顺序表的缺点有两个:
- 一是双链表不支持像顺序表这样的随机访问,也就是下标访问,执行需要随机访问的算法是不合适的。
- 二是由于高速缓存cache每次搬运给寄存器的是一块连续的内存单元供CPU访问,而链表在内存中的存储是非连续的,这样cache搬运效率必然不高(类似于:去一家超市将所有需要的东西买完和去许多家超市将所有需要的东西买完所需要的时间)
此处有疑问的可以去网上搜索CPU访问磁盘数据的过程相关的资料
因此不同的数据结构没有最好,只有根据实际需要选择性价比最高的数据结构方式的说法




 浙公网安备 33010602011771号
浙公网安备 33010602011771号