网络流之最大流

流网络

流网络 $G=(V,E)$ 是一个$\mathbf{\color{Red}{有向图}}$。对于图中的每条边 $(u,v)\in E$ 有一个$\mathbf{\color{Red}{非负}}$的容量（值）$c(u,v) \ge 0$。并且，若边集合 $E$ 中有边 $(u,v)$，则流网络中一定不存在其反向边 $(v,u)$。此外，流网络中可议有环，但不允许有自环。特殊的，若图中有反向边，则可以化为如下形式（$1$ 号边拆为 $2,3$ 号边）。

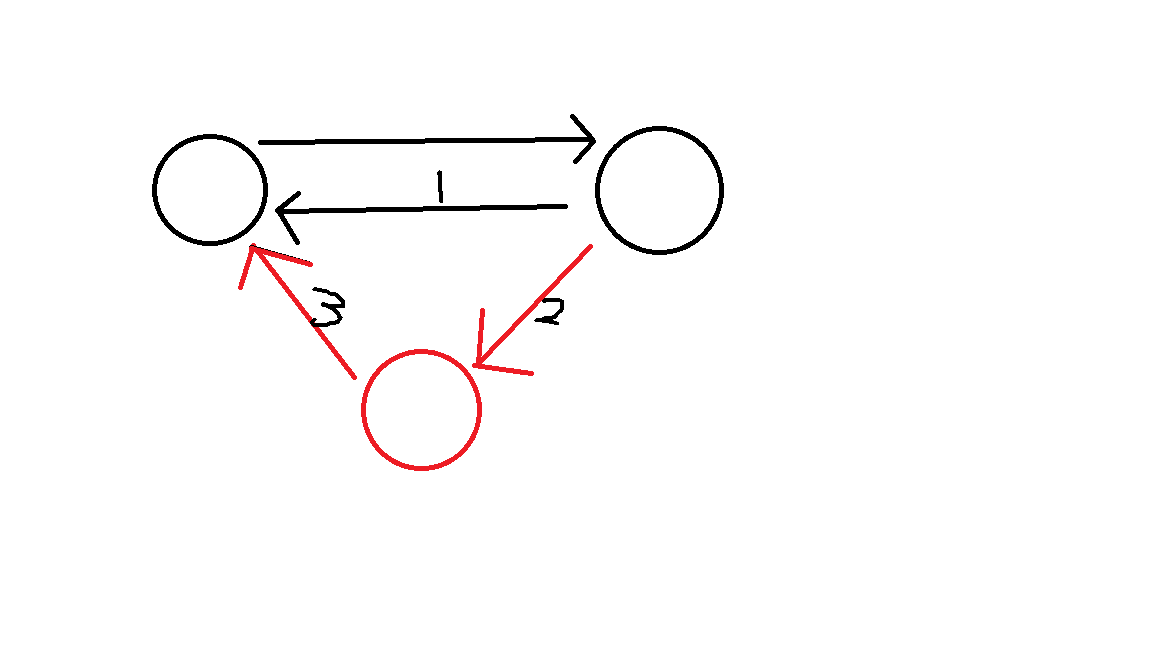
在流网络中，我们分辨出两个特殊的节点：源节点 $s$ 和 汇点 $t$。对于 $\forall v \in V$，都存在从 $s$ 到 $v$，再到 $t$ 的路径（流网络是连通的）。并且，在流网络中，除了源节点外，每个节点都至少有一条入边。

---

 

可行流

对于一个流网络 $G=(V,E)$，其容量函数为 $c$。则 $G$ 的一个可行流（实值函数 $f$）需要满足以下两个条件。

1.容量限制。$\forall u,v \in V$，有 $0 \le f(u,v) \le c(u,v)$。

2.流量守恒。$\forall u,v \in V- \{ s,t \}$，有 $\sum\limits_{v \in V}f(v,u)=\sum\limits_{v \in V}f(u,v)$。

对于一个可行流 $f$，其流量的定义为 $|f|=\sum\limits_{v \in V}f(s,v)-\sum\limits_{v \in V}f(v,s)$。通常，第二项为 $0$（残余网络不是）。此外，由定义易得一个流网络可能有无限个可行流。其中，流量最大的一个可行流被称为最大可行流（最大流）。

---

残余网络

对于一个流网络 $G$ 和该流网络的一个可行流 $f$，有与该可行流相对应的残余网络 $G_f$。

该残存网络的点集与原流网络的点集相同。而构成该残存网络的边不仅有原流网络中的边，还有原流网络中边的反向边。对于残余网络 $G_f$，其残存容量 $c_f(u,v)$ 的定义为：

$c_f(u,v)=\begin{cases}c(u,v)-f(u.v)&(u,v)\in E\\f(v,u)&(v,u)\in E\\0&else\end{cases}$

例如，对于如下流网络和其的一个可行流：

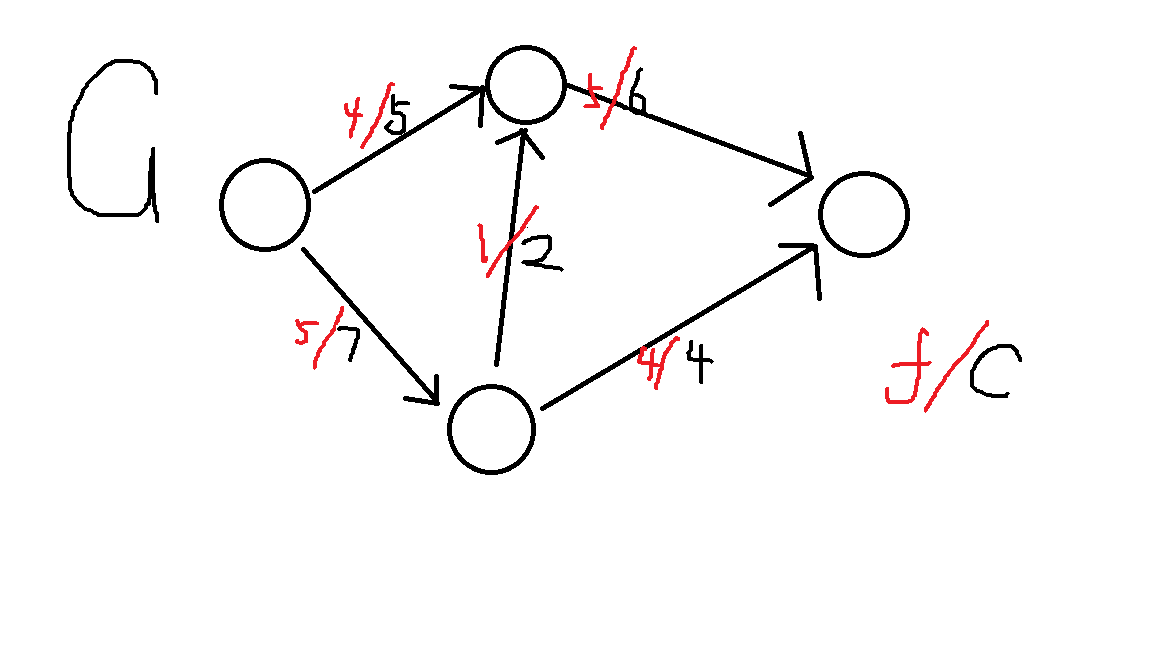
它的残余网络为：

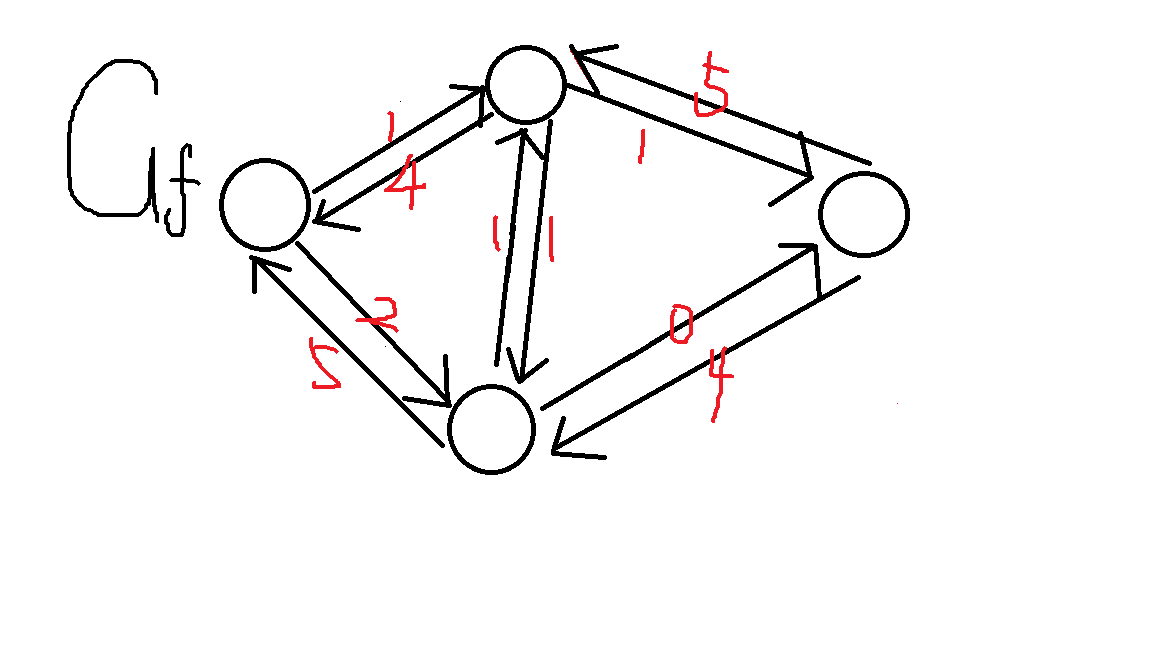
$\mathbf{\color{Purple}{引理\ 1:\ }}$

设 $f'$ 为 $G_f$ 的一个可行流，则 $f \uparrow f'$ 也是 $G$ 的一个可行流，且该可行流的流量 $|f \uparrow f'|=|f|+|f'|$。其中 $f \uparrow f'$ 是流 $f'$ 对流 $f$ 的递增，$(f \uparrow f')(u,v)=f(u,v)+f'(u,v)-f'(v,u)\ ((u,v) \in E)$。 

 证明：

   首先证明其满足容量限制。因为 $f'(v,u) \le c_f(v,u)=f(u,v)$，所以有

$(f \uparrow f')(u,v)=f(u,v)+f'(u,v)-f'(v,u)$

$\ge f(u,v)+f'(u,v)-f(u,v)$

$=f'(u,v) \ge 0$

   同时，还有

$(f \uparrow f')(u,v)=f(u,v)+f'(u,v)-f'(v,u)$

$\le f(u,v)+f'(u,v)$

$\le f(u,v)+c_f(u,v)$

$=f(u,v)+c(u,v)-f(u,v)$

$=c(u,v)$

   故满足容量限制。其次证明流量守恒。因为 $f,f'$遵守流量守恒性质，因此

$\sum\limits_{v \in V}(f \uparrow f')(u,v)=\sum\limits_{v \in V}(f(u,v)+f'(u,v)-f'(v,u))$

$=\sum\limits_{v \in V}f(u,v)+\sum\limits_{v \in V}f'(u,v)-\sum\limits_{v \in V}f'(v,u)$

$=\sum\limits_{v \in V}f(v,u)+\sum\limits_{v \in V}f'(v,u)-\sum\limits_{v \in V}f'(u,v)$

$=\sum\limits_{v \in V}(f(v,u)+f'(v,u)-f'(u,v))$

$=\sum\limits_{v \in V}(f \uparrow f')(v,u)$

   其增加流后的流量证明略。

---

增广路径

对于一个流网络 $G$ 和其的一个可行流 $f$，增广路径 $p$ 是残余网络 $G_f$ 中一条从源点到汇点的$\mathbf{\color{Red}{简单路径}}$。

对于一条增广路径 $p$，能为每条边加上的最大流量为路径 $p$ 的残余容量。其表达式为 $c_f(p)=min\{ c_f(u,v)[(u,v) \in p]\}$。

---

流网络的切割（割）

附：网络流之最小割 常见模型。

流网络 $G=(V,E)$ 的一个割 $(S,T)$ 把点集 $V$ 分为了 $S$ 和 $T=V-S$ 两个集合，使得 $s \in S,t \in T$。定义某个割 $(S,T)$ 的流量（净流量）为 $f(S,T)=\sum\limits_{u \in S}\sum\limits_{v \in T}f(u,v)-\sum\limits_{u \in S}\sum\limits_{v \in T}f(v,u)$。定义割的容量 $c(S,T)=\sum\limits_{u \in S}\sum\limits_{v \in T}c(u,v)$。需要注意的是，割的容量只算 $S$ 到 $T$ 的部分，而割的流量则还要算 $T$ 到 $S$ 的部分（其定义的不对称性）。此外，最小割指最小切割容量。

$\mathbf{\color{Purple}{引理\ 2:\ }}$

设 $f$ 是流网络 $G$ 的一个可行流，$(S,T)$ 是 $G$ 的一个（任意）切割，则 $f(S,T)=|f|$。

证明：

   为方便证明，我们定义如下函数：$X,Y$ 是两个点集且并集为空，表达式$f(X,Y)=\sum\limits_{u \in X}\sum\limits_{v \in Y}f(u,v)-\sum\limits_{u \in  X}\sum\limits_{v \in Y}f(v,u)$。那么我们有：

   1.$f(X,Y)=-f(Y,X)$

   2.$f(X,X)=f(Y,Y)=0$

   3.若还有一个点集 $Z$，$f(Z,X \cup Y)=f(Z,X)+f(Z,Y)$

   因此，我们有

   $f(S,T)+f(S,S)=f(S,S \cup T)=f(S,V)$

$f(S,T)=f(S,V)-f(S,S)$

$f(S,T)=f(S,V)$

$f(S,T)=f(\{ s \},V)+f(S-\{ s \},V)$

   因为$s,t \notin S-\{ s \}$，故这些节点满足流量守恒，故后面一项为 $0$。因此，有

$f(S,T)=f(\{ s \},V)=|f|$（$|f|$ 的定义式）

   证毕。

$\mathbf{\color{Purple}{引理\ 3:\ }}$

流网络 $G$ 中最大流的流量不超过 $G$ 的任意割的容量。

证明：

   $|f|=f(S,T)=\sum\limits_{u \in S}\sum\limits_{v \in T}f(u,v)-\sum\limits_{u \in S}\sum\limits_{v \in T}f(v,u)$

$\le \sum\limits_{u \in S}\sum\limits_{v \in T}f(u,v)$

$\le \sum\limits_{u \in S}\sum\limits_{v \in T}c(u,v)$

$=c(S,T)$（$c(S,T)$ 的定义式）