网络流之最大流附文：上下界问题

无源汇上下界可行流
问题：给定一个包含 $n$ 个点 $m$ 条边的有向图，每条边都有一个流量下界和流量上界 $c,d$。求一种可行方案使得在所有点满足流量平衡条件的前提下，所有边满足流量限制。

建图：新建一个图 $G'$。$G'$ 相对于原图 $G$，把每条边的流量下界调为 $0$ ，把上界调为 $d-c$。那么假若在 $G'$ 上某边的流量值为 $f_0$，则在 $G$ 上，该边的流量值为 $c+f_0$。此时会发现，在 $G'$ 上明显满足容量限制，但不满足流量守恒。那么对于新图上的每个点，如果少进的流量 $f_{in}$（被减掉的 $c$）大于的少出的流量 $f_{out}$，则从 $G'$ 的源点 $S$ 连一条通往该点的容量为 $f_{in}-f_{out}$ 的边，否则连向汇点。那么，对于 $G'$ 的一个最大流，即 $S,T$ 给每个点补的流量刚好与某点的流量差值达到平衡时，映射到 $G$ 上就是一个可行流。

证明：首先证明 $G'$ 的流满足可行流性质。显然，我们的构造已经满足。

   其次，证明 $G'$ 上的任何一个满流（最大流）都是 $G$ 的一个可行流。对于 $G'$ 的满流 $f_{1},...,f_{inf}$，显然对于 $\forall i \ne j$，有 $f_i \ne f_j$。因此，映射到 $G$ 上的可行流也互不相同。而又由于还原后满足容量限制和流量守恒，因此可得这两个集合相等。

   然后，对于 $G$ 的可行流一定是 $G'$ 的满流，我们的构造操作就是直接映射过去的，所以一定满足。证毕。

---

有源汇上下界可行流

问题：给定一个包含 $n$ 个点 $m$ 条边的有向图，每条边都有一个流量下界和流量上界。给定源点 $S$ 和汇点 $T$，求源点到汇点的任何一种可行方案。

建图：我们把问题中给定的 $S$ 和 $T$，在以下论述中称为 $s$ 和 $t$。与无源汇上下界可行流不同的是，$s,t$ 不满足流量守恒。那么我们在原图中连一条从 $t$ 到 $s$，容量范围为 $[0,+inf]$ 的边。那么，这个流网络就成了所有点都满足流量守恒的图。然后再跑无源汇上下界可行流，即可求出。

---

有源汇上下界最大流

问题：给定一个包含 $n$ 个点 $m$ 条边的有向图，每条边都有一个流量下界和流量上界。给定源点 $S$ 和汇点 $T$，求源点到汇点的最大流。

建图：我们把问题中给定的 $S$ 和 $T$，在以下论述中称为 $s$ 和 $t$，而把新图中的超级源点和超级汇点称为 $S$ 和 $T$。先按照有源汇上下界可行流的做法跑一遍，求得答案为 $g_1$。然后删掉 $t$ 连到 $s$ 的边。其次跑 $s$ 到 $t$ 的最大流（找增广路），求得 $s$ 到 $t$ 的流为 $g_2$。那么总答案就是 $g_1+g_2$。

通过以上步骤，我们得出了这个问题中，互相可推的两个集合：原图的可行流和新图中 $s$ 到 $t$ 的可行流。

证明：首先，显然在新图中的最大流满足流的性质。

   其次，证明两个集合间的充要性。我们令原图为 $G$，原图中的一个可行流 $f$，新图为 $G'$，新图中的一个最大流为 $f'$，新图最大流的残余网络为 $G'_{f'}$。

   此时，由于 $f'$ 是最大流，也就是说，在 $G'_{f'}$ 中，以 $S$ 为始的边容量为 $0$。则如果从 $s$ 开始，在 $G'_{f'}$ 上找增广路径，一定不会经过 $S$。对于 $T$ 同理。这是 $(1)$ 结论。

   其次，找 $s$ 到 $t$ 的可行流，实质是不断找 $G'_{f'}$ 上 $s$ 到 $t$ 的增广路径（这是结论 $(2)$），也就是 $G'_{f'}$ 上的某个流，记作 $f'_0$。（也就是 $f'$ 在红框内的流）由于结论 $(1)$ 的支撑，我们可以知道这是成立的（由于 $S,T$ 走不通，所以增广路径可以看做 $S$ 到 $T$ 的增广路径，只是第一段路径和最后一段路径的流量为 $0$。）。然后，由于网络流之最大流引理1，我们有 $f' \uparrow f'_0$ 也是 $G'$ 的一个可行流。

 

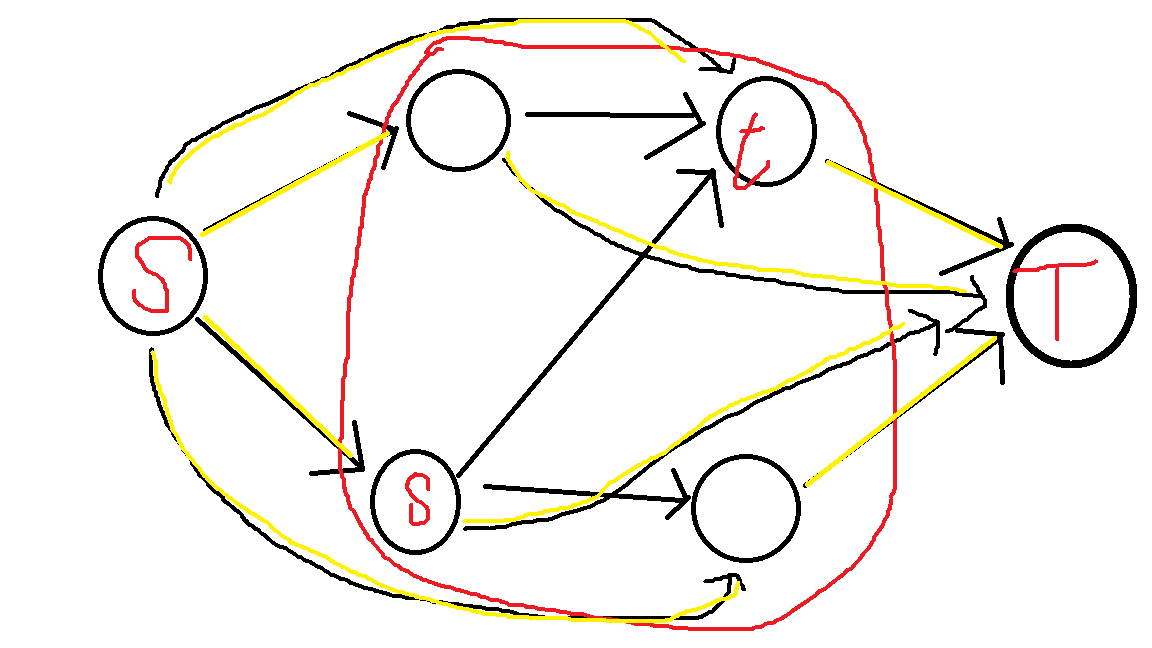
   同时，因为 $(f \uparrow f')(u,v)=f(u,v)+f'(u,v)-f'(v,u)\ ((u,v) \in E)$。放到这个问题里面来看，$f'_0(u,v)$ 和 $f'_0(v,u)$ 在黄色边上的流量为 $0$（结论 $(2)$）。因此，在黄色边上，流量仍然为满。在红色框内，流量才有变化。那么，$f' \uparrow f'_0$ 仍然是 $G'$ 的满流，因此仍然是 $G$ 的可行流。因此可知，$s$ 到 $t$ 的任意可行流（只经过红色框内的可行流）都能映射到 $G$ 的一个可行流上。

   通过上述论证，第二个集合可以推出第一个结论。考虑第一个推第二个。仍然设有一个原图 $G$，其一个可行流 $f$，新图 $G' $和满流 $f'$，残余网络 $G'_{f'}$ ，和 $s$ 到 $t$ 的一个可行流 $f'_0$（仍然可以看作 $S$ 到 $T$ 的特殊增广路径）。 此时 $f'$ 与 $f$ 呈互映射关系。我们再在 $G'$ 上找一个特定的满流 $f''$。则 $\forall f',f' \downarrow f''$ 在 $G'_{f'}$ 中只有红色框流向 $S,T$ 的流和红色框内部流量（因为这两个流都是 $G'$ 上的流，故图中不存在反向边。另外，$f'$ 和 $f''$ 在黄边上都是满流，因此递减后黄边的流量为 $0$，也就是只在红框内有流量）。红色框流出的流量无法流回红色框，因此 $f' \downarrow f''$ 映射到了红框内的一个可行流，即 $s$ 到 $t$ 的一个可行流。也就是说，$s$ 到 $t$ 的可行流能映射 $G'$ 的某个满流，是由于本题的特殊性，黄色边的流量达到上限，满流递减后只剩下红框内的流量了。因此可得，$f$ 唯一映射 $f'$，$f'$ 能映射到 $s$ 到 $t$ 一个的可行流上。

   两个集合互相映射，所以可以推出两个集合相等。证毕。

因此，求 $G$ 的最大流，除了要求出 $G'$ 满流时 $s$ 到 $t$ 的流量，还需求出删掉 $S,T$ 和连的 $t$ 到 $s$ 的边后 $s$ 到 $t$ 的最大流。