2023-2练习
动态规划
阿巴阿巴
核心套路
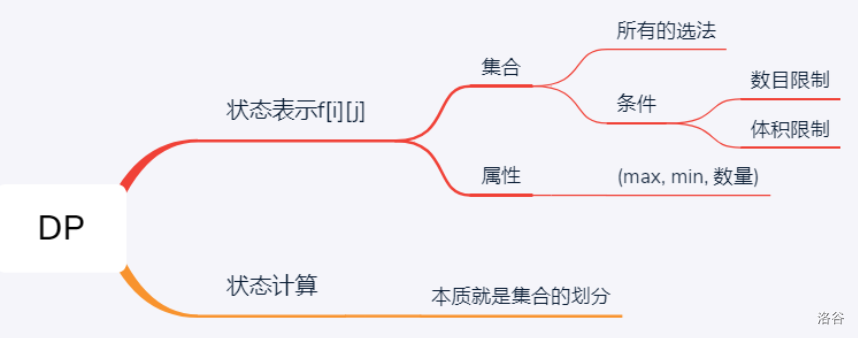
问题:集合如何划分
-
一般原则:
不重(不一定都要满足,一般求个数时要满足) 不漏(必满足) -
如何将现有的集合划分为更小的子集,使得所有子集都可以计算出来。
-
一般地,正序寻找最后一个不同点,倒序寻找第一个不同点
2023-2-13
特点:每个物品仅能使用一次
思:每个物品有选和不选两种状态,若暴力枚举,时间复杂度为\(O(2^n)\),需对其进行优化。
- 设置状态\(f[i][j]\)
表示从编号为1~i的物品中选择且物品总体积\(v≤j\),它的值是这个集合中每一个选法的最大值
- 状态转移方程
不选:值为前一个集合最大值 \(f[i][j]=f[i-1][j]\)
选择:\(f[i][j]=f[i-1][j-v[i]]+w[i]\)
所以转移方程为\(f[i][j]=max(f[i-1][j], f[i-1][j-v[i]]+w[i])\)
不要忘记设置初始状态\(f[0][0]=0\)
//代码如下
f[i][j]=f[i-1][j];
if(j>=v[i]){//注意j-v[i]不能越界,背包满了
f[i][j]=max(f[i-1][j],f[i-1][j-v[i]]+w[i]);
}
小寄巧: memset(f,0xcf,sizeof f);初始化为负无穷
二维朴素版本
#include <bits/stdc++.h>
using namespace std;
const int N=1e3+10;
int n,V,w[N],v[N],f[N][N];
int main()
{
cin>>n>>V;
for(int i=1;i<=n;i++) cin>>v[i]>>w[i];
memset(f,0xcf,sizeof f);
f[0][0]=0;
for(int i=1;i<=n;i++){
for(int j=0;j<=V;j++){//正序倒序均可
f[i][j]=f[i-1][j];
if(j>=v[i]){
f[i][j]=max(f[i-1][j],f[i-1][j-v[i]]+w[i]);
}
}
}
int ans=0;
for(int i=0;i<=V;i++) ans=max(ans,f[n][i]);
cout<<ans;
return 0;
}
将状态\(f[i][j]\)优化到一维\(f[j]\),实际上只需要做一个等价变形。
为什么可以这样变形呢?我们定义的状态\(f[i][j]\)可以求得任意合法的\(i\)与\(j\)最优解,但题目只需要求得最终状态\(f[n][m]\),因此我们只需要一维的空间来更新状态。
1 .状态\(f[j]\)定义:\(N\)件物品,背包容量j下的最优解。
2 . 注意枚举背包容量\(j\)必须从\(V\)开始。
3 . 为什么一维情况下枚举背包容量需要逆序?在二维情况下,状态\(f[i][j]\)是由上一轮i - 1的状态得来的,\(f[i][j]\)与\(f[i - 1][j]\)是独立的。而优化到一维后,如果我们还是正序,则有\(f[较小体积]\)更新到\(f[较大体积]\),则有可能本应该用第i-1轮的状态却用的是第i轮的状态。
4.例如,一维状态第\(i\)轮对体积为 \(3\)
的物品进行决策,则\(f[7]\)由\(f[4]\)更新而来,这里的\(f[4]\)正确应该是\(f[i - 1][4]\),但从小到大枚举j这里的f[4]在第i轮计算却变成了\(f[i][4]\)。当逆序枚举背包容量j时,我们求\(f[7]\)同样由\(f[4]\)更新,但由于是逆序,这里的\(f[4]\)还没有在第\(i\)轮计算,所以此时实际计算的\(f[4]\)仍然是\(f[i - 1][4]\)。
5.简单来说,一维情况正序更新状态\(f[j]\)需要用到前面计算的状态已经被「污染」,逆序则不会有这样的问题。
\(f[i-1][j]=f[j],f[i-1][j-v[i]]=f[j-v[i]]\)
状态转移方程为:\(f[j] = max(f[j], f[j - v[i]] + w[i])\)
一维版本
#include <bits/stdc++.h>
using namespace std;
const int N=1e3+10;
int n,V,v[N],w[N],f[N];
int main()
{
cin>>n>>V;
for(int i=1;i<=n;i++) cin>>v[i]>>w[i];
for(int i=1;i<=n;i++){
for(int j=V;j>=v[i];j--){//注意逆序
f[j]=max(f[j],f[j-v[i]]+w[i]);
}
}
//cout<<f[V];
int ans=0;
for(int i=0;i<=V;i++) ans=max(ans,f[i]);
cout<<ans;
return 0;
}
特点:每个物品可重复使用
不选:值为前一个集合最大值 \(f[i][j]=f[i-1][j]\)
选择:\(f[i][j]=f[i][j-v[i]]+w[i]\)
所以转移方程为\(f[i][j]=max(f[i-1][j],f[i][j-v[i]]+w[i])\)
- 想求 \(f[i][j]\),
要先求\(f[i][j-v[i]]\),,两者都是\(f[i]\),也就是在同一层,所以只能正序更新。
二维朴素版
#include<bits/stdc++.h>
using namespace std;
const int N = 1e3+10;
int n, V;
int dp[N][N], v[N], w[N];
int main(){
cin >> n >> V;
for(int i = 1; i <= n; i ++ )
cin >> v[i] >> w[i];
for(int i = 1; i <= n; i ++ ){
for(int j = 0; j <= V; j ++ ){//注意正序
dp[i][j] = dp[i - 1][j];
if(j >= v[i])
dp[i][j] = max(dp[i][j], dp[i][j - v[i]] + w[i]);
}
}
cout << dp[n][V] << endl;
return 0;
}
与01背包类似
\(f[i][j]=f[j],f[i][j-v[i]]=f[j-v[i]]\)
转移方程为$ f[j]=max(f[j],f[j-v[i]]+w[i])$
与01背包不同,要正序
一维版
#include<bits/stdc++.h>
using namespace std;
const int N = 1e3+10;
int n, V;
int dp[N];
int main(){
cin >> n >> V;
for(int i = 1; i <= n; i ++ ){
int v, w;
cin >> v >> w;
for(int j = v; j <= V; j ++ ){//注意正序
dp[j] = max(dp[j], dp[j - v] + w);
}
}
cout << dp[V] << endl;
}
逐步优化
2023.2.14
区:子段和子序列
\(a={1,1,4,5,1,4}\)//doge
子段:连续的一段,\(e.g.\) [1,1,4],[1,4,5] ,[5,1,4]
子序列:不一定连续,\(e.g.\) [1,4,4],[1,1,1],[1,5,1]
子段一定是子序列
这里上升子序列是严格单调递增(不能相等
思:
从5向前找,有 [5] ,\([4,5],[1,4,5],[1,4,5]\)符合上升条件
注意:只有自己也是一种情况
设置状态:\(f[i]\)表示从第\(i\)个数向前找,它的值为最大上升子序列的长度
状态转移:
符合升序,则选择 \(f[i]=f[j]+1(i>j)\)
所以方程为\(f[i]=max(f[i],f[j]+1)\)
- 模板
#include <bits/stdc++.h>
using namespace std;
int f[10000],a[10000],n;
int main(){
memset(a,0xcf,sizeof a);//防止数据的值为负数或0,出现问题
cin>>n;
for(int i=1;i<=n;i++) cin>>a[i];
for(int i=1;i<=n;i++){
for(int j=i-1;j>=0;j--){//从i-1往前扫,j=0即可计算只有i的情况f[j]+1=1
if(a[i]>a[j]) f[i]=max(f[i],f[j]+1);//要符合升序
}
}
int ans=0;
for(int i=1;i<=n;i++) ans=max(ans,f[i]);//f[n]未必是最大值
cout<<ans;
return 0;
}
2023.2.16
- 区间DP
区间DP+前缀和
规定每次只能选相邻的2堆合并成新的一堆,是连续的。
所以数组开二倍,变成一个环。

样例:4 5 9 4
可以1和2合并,3和4合并,2和3合并,总价=(4+5)+(9+4)+(4+5+9+4)=44,
也可以2和3合并,1和2,3和4,总价=(5+9)+(4+5+9)+(9+5+4+4)=54,
求出总价最大/最小。
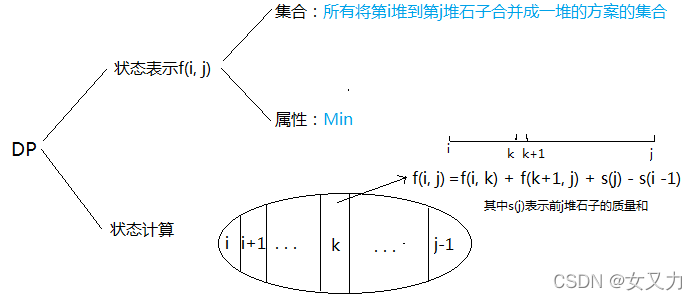
设状态:
\(f[i][j]\) 表示一个区间的左端点i,为右端点j,存最大方案数,(\(g[i][j]\)反之.
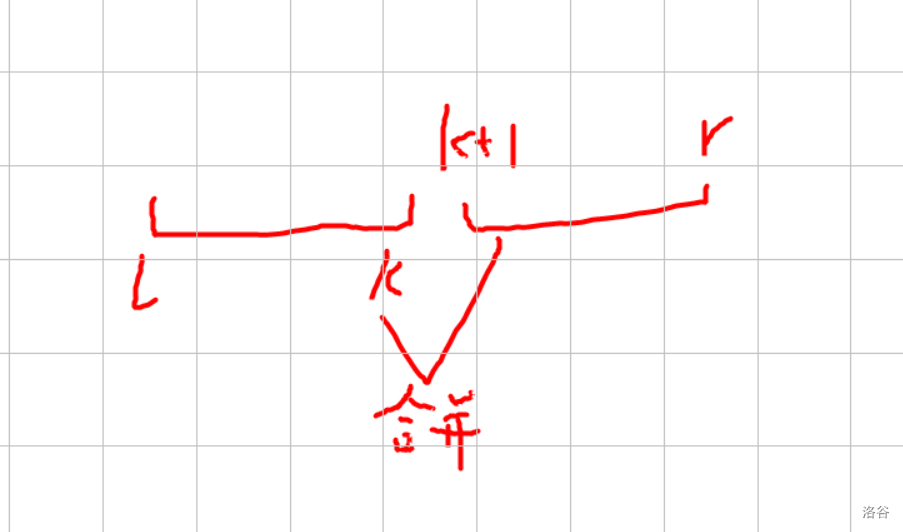
转移:
枚举区间(l,r),然后枚举l和r之间的k点。
\(f[l][r]=\max(f[l][r],f[l][k]+f[k+1][r]+s[r]-s[l-1])\)
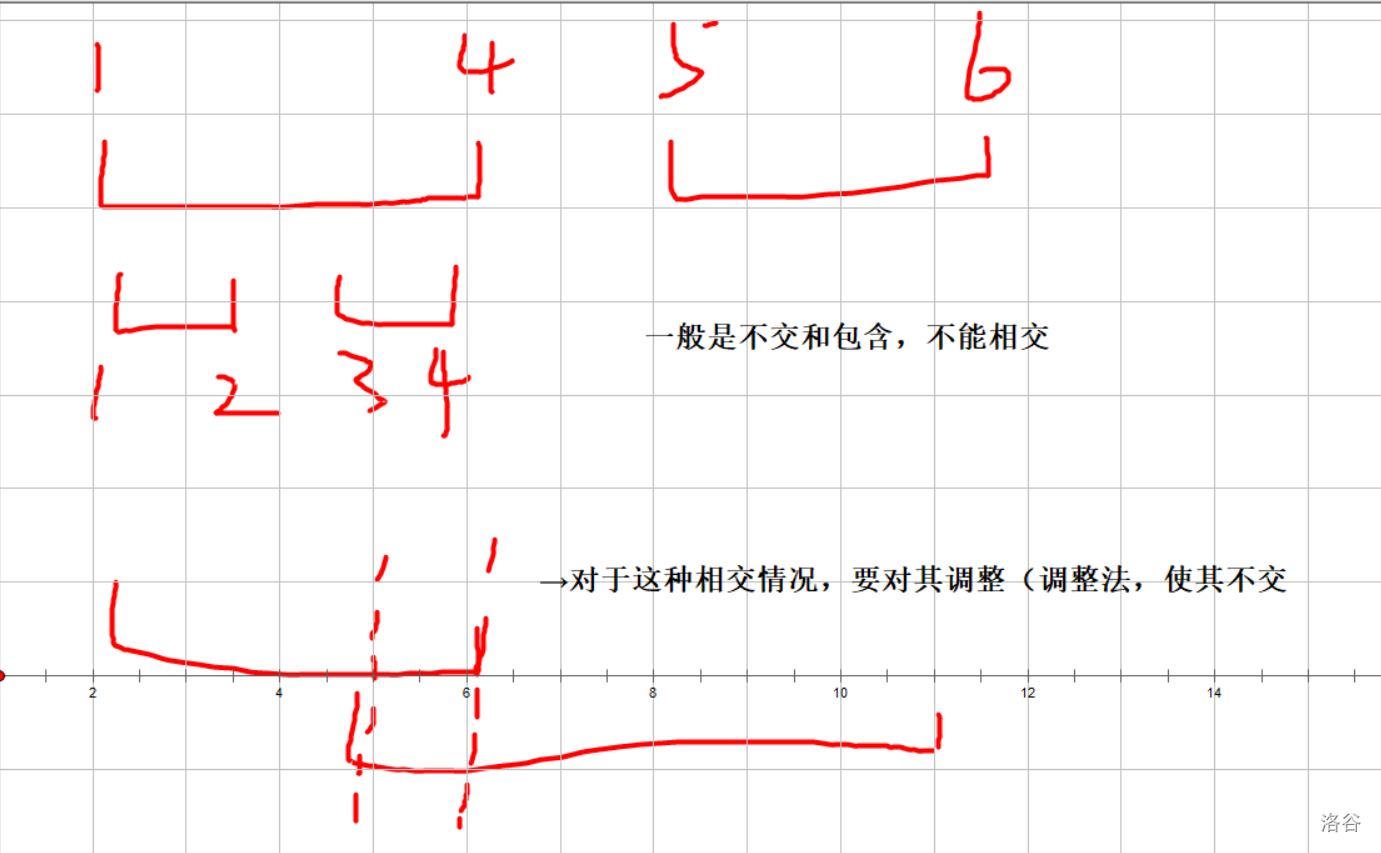
区间DP应用情况:
#include <bits/stdc++.h>
#define cin std::cin
#define cout std::cout
#define endl std::endl
#define max std::max
#define min std::min
namespace lcj{
const int N=210;
int n,a[N],f[N][N],g[N][N],s[N];
void main(){
cin>>n;
for(int i=1;i<=n;i++){
cin>>a[i];
a[i+n]=a[i];
}
for(int i=1;i<=2*n;i++) s[i]+=s[i-1]+a[i];
memset(f,0xcf,sizeof f);memset(g,0x3f,sizeof g);//初始化
for(int i=1;i<=2*n;i++) f[i][i]=g[i][i]=0;
for(int i=2;i<=n;i++){//枚举长度为i的区间
for(int l=1;l+i-1<=2*n;l++){//注意细节
int r=l+i-1;//计算r,不要忘-1。
for(int k=l;k<r;k++){//k<r
f[l][r]=max(f[l][r],f[l][k]+f[k+1][r]+s[r]-s[l-1]);
g[l][r]=min(g[l][r],g[l][k]+g[k+1][r]+s[r]-s[l-1]);
}
}
}
int maxv=INT_MIN,minv=INT_MAX;//INT_MIN是个常数,int的最小值,选最大值用,不能加,会爆,
for(int i=1;i<=n;i++){
maxv=max(maxv,f[i][i+n-1]);//区间长度i+n-1,不要忘-1,EXP++;
minv=min(minv,g[i][i+n-1]);
}
cout<<minv<<endl<<maxv;
}
}
signed main(){
lcj::main();
return 0;
}
参考:
AcWing 2. 01背包-打印dp理解用一维数组为何要逆序更新


 浙公网安备 33010602011771号
浙公网安备 33010602011771号