牛客刷题-Day30

牛客刷题-Day30

今日刷题：\(1056-1060\)

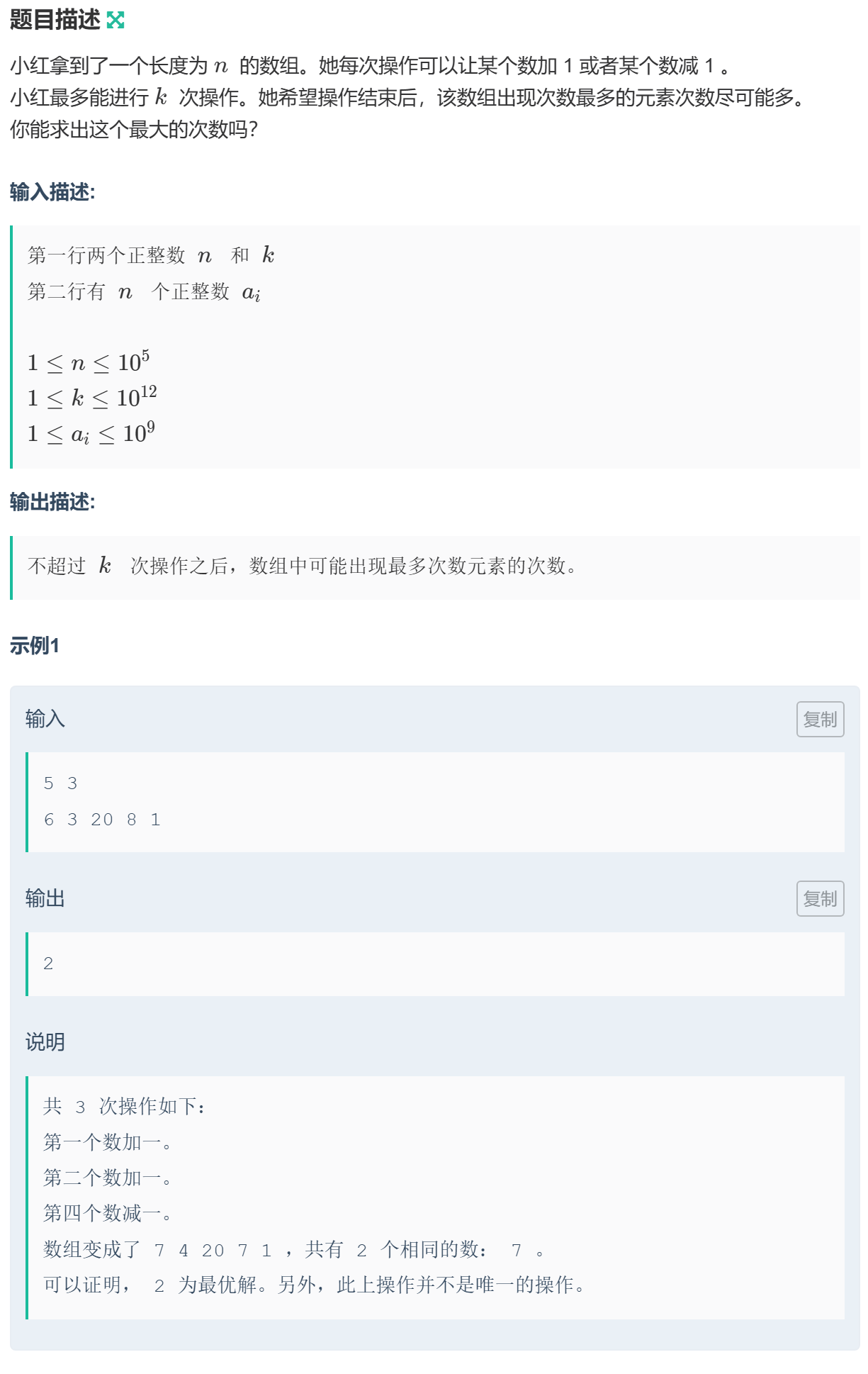
1056 习题-加减

解题思路

双指针：将数组递增排序，如果希望经过操作之后，某个数出现的尽可能多，其必出现在某段连续的区间，且最终变成的数为该区间的中位数。
引理 1：最优解对应排序数组中的连续区间

设原数组排序后为 \(a_1 \le a_2 \le \cdots \le a_n\)
假设在某个最优方案中，选择了一组下标集合 \(S\)，
将这些位置的数都修改为同一个值 \(x\)，且 \(|S|\) 最大、总代价不超过 \(k\)。
若 \(S\) 在排序数组中不是连续区间，
则存在下标 \(i < j < k\)，满足 \(i, k \in S\)，但 \(j \notin S\)。
由于 \(a_i \le a_j \le a_k\)，有 \(|a_j - x| \le \max(|a_i - x|, |a_k - x|\)
将 \(j\) 加入集合 \(S\)，并同样修改为 \(x\)，新增代价为 \(|a_j - x|\)，但出现次数增加了 \(1\)，且新增代价不超过原集合中某一端点的代价。
因此，在不超过代价约束 \(k\) 的前提下，
可以构造出一个包含更多元素的方案，
这与原方案的最优性（\(|S|\) 最大）矛盾。
故在任一最优方案中，
被修改为同一数值的元素在排序数组中必构成一段连续区间 \([l, r]\)。

引理 2：固定区间时，中位数使总代价最小

对任意固定的连续区间 \([l, r]\)，考虑函数 \(f(x) = \sum_{i=l}^{r} |a_i - x|\)
该函数是关于 \(x\) 的凸函数。
当 \(x\) 位于区间中位数位置时，左右两侧元素个数相等（或仅差 \(1\)），此时任意向左或向右微小移动 \(x\)，都会使得距离增加的一侧人数不少于减少的一侧人数，从而使 \(f(x)\) 增大。
因此，当区间长度为奇数时，\(x = a_{(l+r)/2}\) 唯一使 \(f(x)\) 最小；
当区间长度为偶数时，任意 \(x \in [a_{(l+r)/2}, a_{(l+r)/2+1}]\) 均为最优解，取其中任一值即可。

在总代价不超过 \(k\) 的前提下，若希望经过修改后某个数出现次数尽可能多，则最优方案必然对应排序数组中的一段连续区间 \([l, r]\)，且最终修改成的数应取该区间的中位数。
据此，只需枚举区间左端点并扩展右端点，并利用前缀和计算将区间内所有数改为中位数的最小代价，即可在 \(O(n)\) 时间内求解。

C++ 代码

#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
typedef long long LL;

int n;
LL k, a[N], sum[N];

bool check(int l, int r) {
    int mid = (l + r) >> 1;
    // [l, mid]
    LL lsum = a[mid] * (mid - l + 1) - (sum[mid] - sum[l - 1]);
    // [mid + 1, r]
    LL rsum = (sum[r] - sum[mid]) - a[mid] * (r - mid);
    return lsum + rsum <= k;
}

int main() {
    scanf("%d%lld", &n, &k);
    for (int i = 1; i <= n; i++)
        scanf("%lld", &a[i]);
    sort(a + 1, a + n + 1);
    for (int i = 1; i <= n; i++)
        sum[i] = sum[i - 1] + a[i];
    int res = 0;
    for (int i = 1, j = 1; i <= n; i++) {
        while (j <= n && check(i, j)) {
            res = max(res, j - i + 1);
            j++;
        }
    }
    printf("%d\n", res);
    return 0;
}

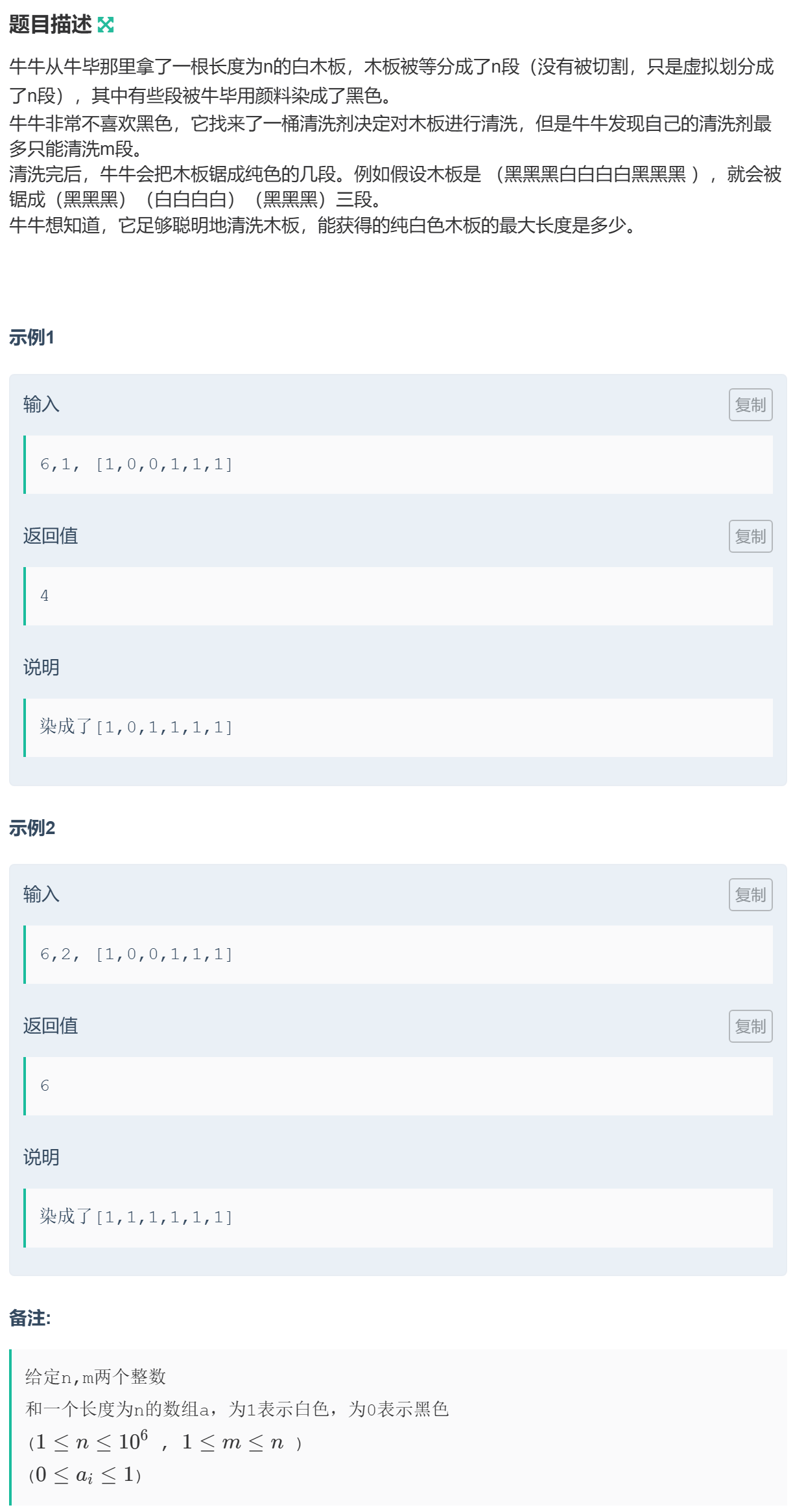
1057 习题-牛牛的木板

解题思路

双指针：移动右指针 \(i\)，当清洗次数大于 \(m\) 时，移动左指针直到清洗次数不超过 \(m\)，更新答案。

C++ 代码

class Solution {
public:
    int solve(int n, int m, vector<int>& a) {
        // write code here
        int cnt = 0, res = 0;
        for (int i = 0, j = 0; i < n; i++) {
            if (!a[i])
                cnt++;
            while (cnt > m) {
                if (!a[j])
                    cnt--;
                j++;
            }
            res = max(res, i - j + 1);
        }
        return res;
    }
};

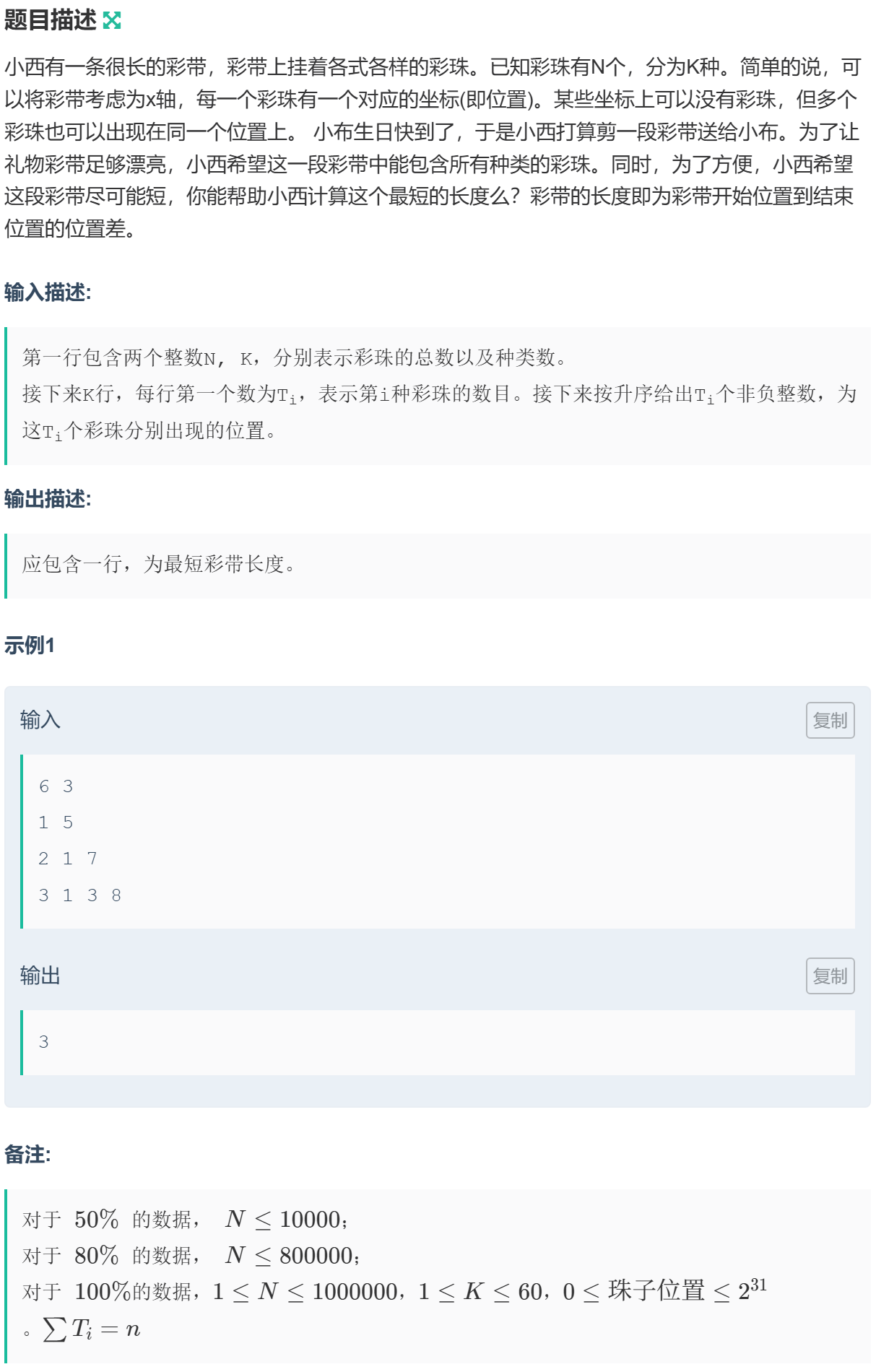
1058 习题-[SCOI2009]生日礼物

解题思路

双指针：将所有的灯按照位置从小到大排序，然后移动右指针 \(i\)，当满足含有所有种类的灯时，移动左指针直到无法满足条件，在左指针移动过程中更新答案。

C++ 代码

#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 10, M = 110;

int n, m, cnt, c[M];
struct Light {
    int pos, id;
} a[N];

bool check() {
    int res = 0;
    for (int i = 1; i <= m; i++)
        if (c[i])
            res++;
    return res == m;
}

bool cmp(Light a, Light b) {
    return a.pos <= b.pos;
}

int main() {
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= m; i++) { // m 种彩灯
        int T;
        scanf("%d", &T);
        for (int j = 1; j <= T; j++) {
            int p;
            scanf("%d", &p); // 彩灯位置
            a[++cnt] = {p, i};
        }
    }
    int res = 1e9;
    sort(a + 1, a + cnt + 1, cmp);
    for (int i = 1, j = 1; i <= cnt; i++) {
        c[a[i].id]++;
        while (check() && j <= cnt) {
            res = min(res, a[i].pos - a[j].pos);
            c[a[j].id]--;
            j++;
        }
    }
    printf("%d\n", res);
    return 0;
}

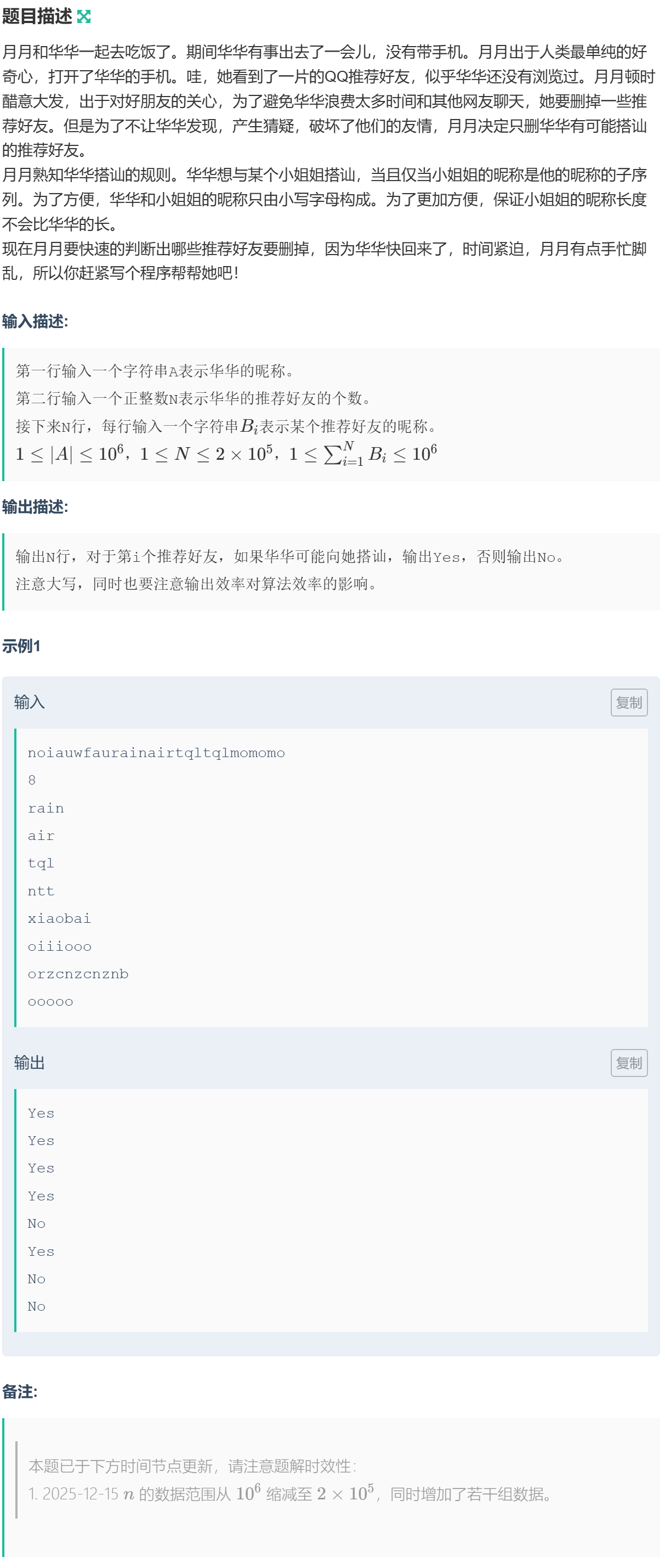
1059 习题-月月查华华的手机

解题思路

字符串 \(a\) 为 \(A\) 的子序列，则从 \(A\) 中取出若干元素按照其在 \(A\) 中的顺序组合之后为 \(a\)。
二分：首先 \(a\) 长度不大于 \(A\) 且 \(a\) 中每个元素的个数不能超过 \(A\) 中对应元素的个数，否则 \(A\) 一定凑不出来 \(a\)。
统计字符串 \(A\) 的所有字母的个数以及在字符串中出现的位置。依次判断 \(a\) 的每个元素在 \(A\) 中出现的次序，在确定位置时尽可能取最小值，且不能小于前一个元素的位置，因此使用 \(last\) 变量记录 \(a\) 上一个元素出现的位置，则当前元素出现的位置至少为 \(last+1\)，每次找位置都使用二分来找符合条件的位置。

C++ 代码

#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 10, M = 26;

int q;
string s;
vector<int> pos[M]; // pos[i] 存储字母 i 的位置 
                    // pos[i][0] 存储 i 的个数
int cnt[M];

int main() {
    cin >> s;
    for (int i = 0; i < M; i++)
        pos[i].push_back(0);
    for (int i = 0; s[i]; i++) { // 初始化
        pos[s[i] - 'a'][0]++;
        pos[s[i] - 'a'].push_back(i);
    }
    cin >> q;
    while (q--) {
        memset(cnt, 0, sizeof cnt);
        string t;
        cin >> t;
        if (t.size() > s.size()) { // 比原串长
            puts("No");
            continue;
        }
        bool flag = true;
        for (int i = 0; t[i]; i++)
            cnt[t[i] - 'a']++;
        for (int i = 0; i < M; i++)
            if (cnt[i] > pos[i][0]) { // t 中某个字母个数比 s 的多
                flag = false;
                break;
            }
        if (!flag) {
            puts("No");
            continue;
        }
        int last = -1; // 上一个字母出现的位置
        for (int i = 0; t[i]; i++) {
            int l = 1, r = pos[t[i] - 'a'].size() - 1;
            while (l < r) {
                int mid = l + r >> 1;
                if (pos[t[i] - 'a'][mid] >= last + 1)
                    r = mid;
                else
                    l = mid + 1;
            }
            if (pos[t[i] - 'a'][l] >= last + 1)
                last = pos[t[i] - 'a'][l];
            else {
                flag = false;
                break;
            }
        }
        if (!flag) {
            puts("No");
        } else {
            puts("Yes");
        }
    }
    return 0;
}

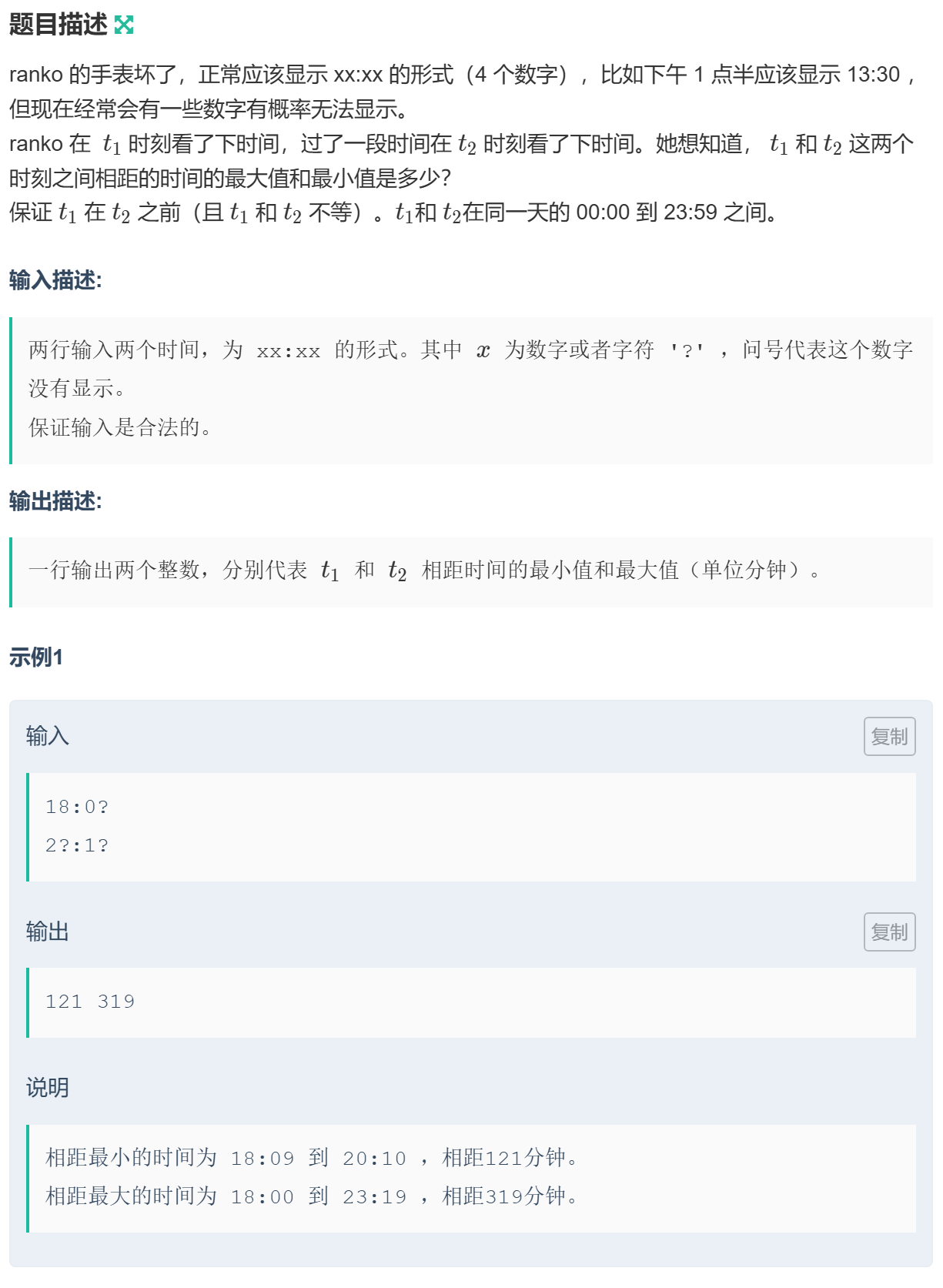
1060 习题-ranko的手表

解题思路

枚举：枚举出两个时间所有合法的具体时间，然后换算为分钟，保证 \(t_1<t_2\)，计算差值，更新答案。

C++ 代码

#include <bits/stdc++.h>
using namespace std;

string a, b;

bool check(char i, char j, char p, char q, string s) {
    if ((i == s[0] || s[0] == '?') 
        && (j == s[1] || s[1] == '?') 
        && (p == s[3] || s[3] == '?')
        && (q == s[4] || s[4] == '?'))
        return true;
    return false;
}

vector<pair<int, int>> get(string s) {
    vector<pair<int, int>> res;
    for (char i = '0'; i <= '2'; i++)
        for (char j = '0'; j <= '9'; j++) {
            int x = (i - '0') * 10 + (j - '0');
            if (x > 23)
                continue;
            for (char p = '0'; p <= '5'; p++)
                for (char q = '0'; q <= '9'; q++) {
                    int y = (p - '0') * 10 + (q - '0');
                    if (check(i, j, p, q, s)) {
                        res.push_back({x, y});
                    }
                }
        }
    return res;
}

int main() {
    cin >> a >> b;
    vector<pair<int, int>> x = get(a), y = get(b);
    int mmax = 0, mmin = 24 * 60;
    for (int i = 0; i < x.size(); i++)
        for (int j = 0; j < y.size(); j++) {
            int t1 = x[i].first * 60 + x[i].second, t2 = y[j].first * 60 + y[j].second;
            if (t1 < t2) {
                mmax = max(mmax, t2 - t1);
                mmin = min(mmin, t2 - t1);
            }
        }
    printf("%d %d", mmin, mmax);
    return 0;
}