牛客刷题-Day29

牛客刷题-Day29

今日刷题：\(1051-1055\)

1051 习题-数学考试

解题思路

动态规划：枚举区间的分界点 \(i\)，先分别求得左侧 \([1,i-1]\) 和右侧 \([i,n]\) 两个区间内长度为 \(k\) 的子区间的最大值，然后求和。

C++ 代码

#include <bits/stdc++.h>
using namespace std;
const int N = 2e5 + 10;
typedef long long LL;

int n, k, T;
LL a[N], l[N], r[N];

int main() {
    scanf("%d", &T);
    while (T--) {
        memset(l, -0x3f, sizeof l);
        memset(r, -0x3f, sizeof r);
        scanf("%d%d", &n, &k);
        for (int i = 1; i <= n; i++) {
            scanf("%lld", &a[i]);
            a[i] += a[i - 1];
        }
        // i 左侧长度为 k 的区间最大值
        for (int i = k; i <= n - k; i++)
            l[i] = max(l[i - 1], a[i] - a[i - k]);
        // i 右侧长度为 k 的区间最大值
        for (int i = n - k + 1; i > k; i--)
            r[i] = max(r[i + 1], a[i + k - 1] - a[i - 1]);
        LL res = -1e18;
        for (int i = k; i <= n - k + 1; i++)
            res = max(res, l[i - 1] + r[i]);
        printf("%lld\n", res);
    }
    return 0;
}

1052 习题-Xorto

解题思路

位运算：题目要求有多少对互不重叠的非空区间，使得两个区间内的数的异或和为0，即求得有多少对互不重叠的非空区间的异或值相等。
首先，前缀和预处理区间异或值。枚举分界点 \(r\)，然后枚举 \(l\)，统计 \([l,r]\) 的区间异或值。然后枚举 \(k\)，看区间 \([r+1,k]\) 的异或值与统计的 \([l,r]\) 的区间异或值有多少相等。

C++ 代码

#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;

int n, a[N], sum[N];
map<int, int> cnt;

int main() {
    scanf("%d", &n);
    for (int i = 1; i <= n; i++) {
        scanf("%d", &a[i]);
        sum[i] = sum[i - 1] ^ a[i];
    }
    long long res = 0;
    for (int r = 1; r <= n; r++) {
        for (int l = r; l >= 1; l--) // 统计以 r 为右端点区间异或值 
            cnt[sum[r] ^ sum[l - 1]]++;
        for(int k = r + 1; k <= n; k++) // r 右侧区间 [r + 1, k]
            res += cnt[sum[k] ^ sum[r]];
    }
    printf("%lld\n", res);
    return 0;
}

1053 习题-仓库选址

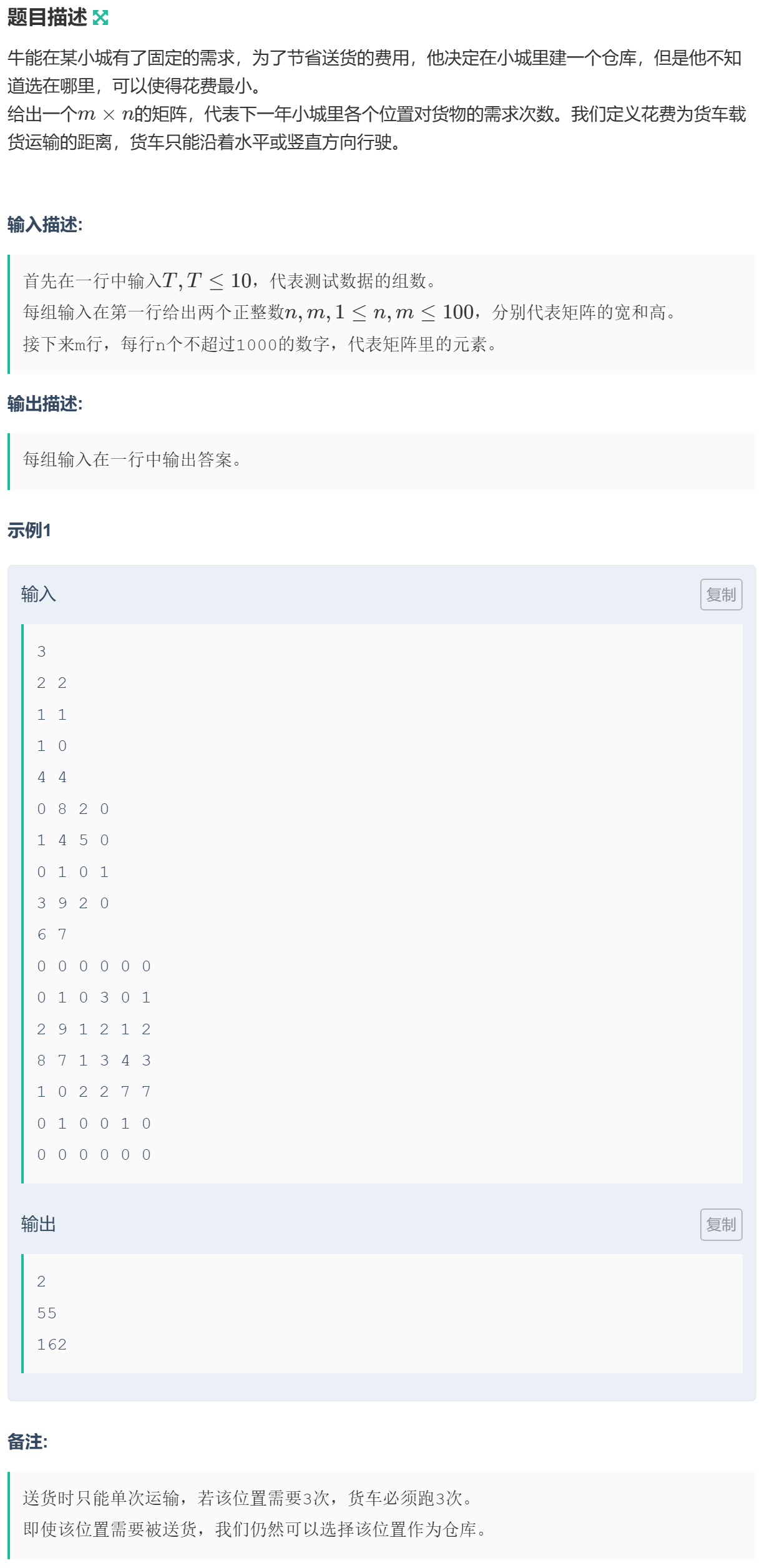
解题思路

枚举：暴力枚举选址点，然后计算花费，取最小值。

C++ 代码

#include <bits/stdc++.h>
using namespace std;
const int N = 110;

int T, a[N][N];

int main() {
    scanf("%d", &T);
    while (T--) {
        int n, m;
        scanf("%d%d", &n, &m);
        for (int i = 1; i <= m; i++)
            for (int j = 1; j <= n; j++)
                scanf("%d", &a[i][j]);
        long long res = 1e18;
        for (int x = 1; x <= m; x++)
            for (int y = 1; y <= n; y++) {
                long long sum = 0;
                for (int i = 1; i <= m; i++) {
                    for (int j = 1; j <= n; j++)
                        sum += a[i][j] * (abs(x - i) + abs(y - j));
                }
                res = min(res, sum);
            }
        printf("%lld\n", res);
    }
    return 0;
}

1055 习题-字符串

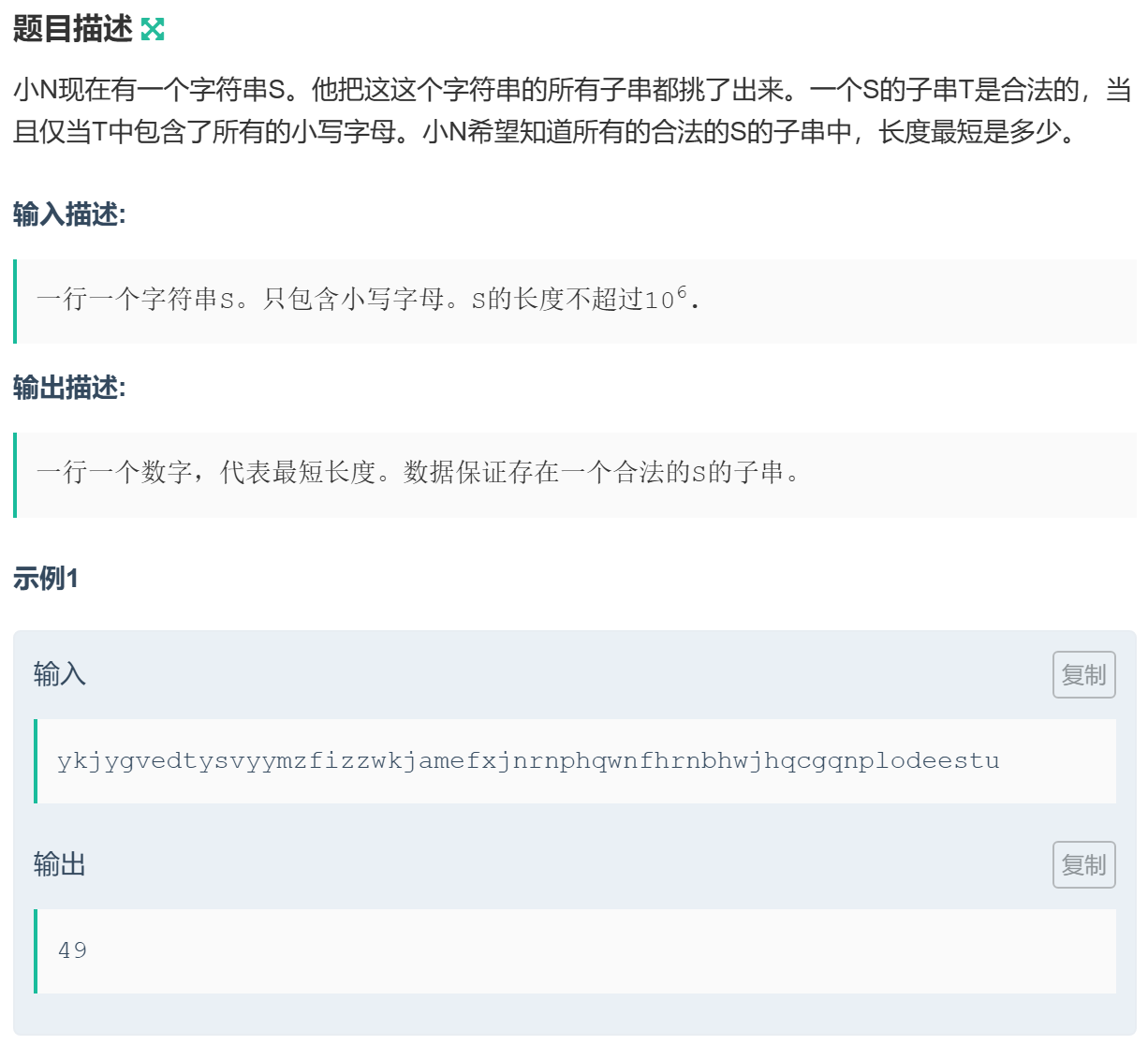
解题思路

双指针：假设 \(i\) 为左指针，\(j\) 为右指针。首先移动 \(j\)，找到第一个 \(j\) 使得 \([i,j)\) 这段字串满足含有 \(26\) 格个小写字母，此时更新答案，然后移动一次左指针 \(i\)，循环往复。

C++ 代码

#include <bits/stdc++.h>
using namespace std;

string S;
int cnt[26];

bool check() {
    int c = 0;
    for (int i = 0; i < 26; i++)
        if (cnt[i])
            c++;
    return c == 26;
}

int main() {
    cin >> S;
    int res = 1e6;
    for (int i = 0, j = 0; S[i]; i++) {
        while (!check() && S[j]) {
            cnt[S[j] - 'a']++;
            j++;
        }
        // cout << i << ' ' << j << ' ' << check() << endl;
        if (check())
            res = min(res, j - i);
        cnt[S[i] - 'a']--;
    }
    printf("%d\n", res);
    return 0;
}