牛客刷题-Day28

牛客刷题-Day27

今日刷题：\(P-S\)

P 区区区间间间

解题思路

本题需要求出区间的最大值与最小值差的和，即则本题即为所有区间的最大值之和减去所有区间的最小值之和。一般这种题目都可以考虑某个元素的贡献度，则本题考虑每个元素在哪些区间为最大值，哪些区间为最小值，然后计算区间个数。
对于元素 \(a_i\)，其作为区间最大值，可以覆盖 \([lmax,rmax]\)，作为区间最小值，可以覆盖 \([lmin,rmin]\)，则其作为最大值覆盖区间个数为 \((i-lmax+1) * (rmax-i+1)-1\)，因为左边可以有 \([0,i-lmax+1]\) 个数，右边可以有 \([0,rmax-i+1]\) 个数，注意需要去除都不取的情况。同理，可取得其作为最小值覆盖区间个数。

C++ 代码

#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
typedef long long LL;

int T, n;
LL a[N];
// lmin, rmin 表示 a[i] 为 [lmin[i], rmin[i]] 最小的数
// lmax, rmax 表示 a[i] 为 [lmax[i], rmax[i]] 最大的数
LL lmax[N], lmin[N], rmax[N], rmin[N];

void solve() {
    scanf("%d", &n);
    for (int i = 1; i <= n; i++)
        scanf("%lld", &a[i]);
    stack<LL> stk;
    for (int i = 1; i <= n; i++) { // 左边第一个小于 a[i] 的数
        while (!stk.empty() && a[stk.top()] >= a[i])
            stk.pop();
        lmin[i] = stk.empty() ? 1 : stk.top() + 1;
        stk.push(i);
    }
    while (!stk.empty())
        stk.pop();
    for (int i = n; i >= 1; i--) { // 右边第一个小于 a[i] 的数
        while (!stk.empty() && a[stk.top()] > a[i])
            stk.pop();
        rmin[i] = stk.empty() ? n : stk.top() - 1;
        stk.push(i);
    }
    while (!stk.empty())
        stk.pop();
    for (int i = 1; i <= n; i++) { // 左边第一个大于 a[i] 的数
        while (!stk.empty() && a[stk.top()] <= a[i])
            stk.pop();
        lmax[i] = stk.empty() ? 1 : stk.top() + 1;
        stk.push(i);
    }
    while (!stk.empty())
        stk.pop();
    for (int i = n; i >= 1; i--) { // 右边第一个大于 a[i] 的数
        while (!stk.empty() && a[stk.top()] < a[i])
            stk.pop();
        rmax[i] = stk.empty() ? n : stk.top() - 1;
        stk.push(i);
    }
    LL res = 0;
    for (int i = 1; i <= n; i++)
        res -= a[i] * ((LL)(i - lmin[i] + 1) * (rmin[i] - i + 1) - 1);
    for (int i = 1; i <= n; i++)
        res += a[i] * ((LL)(i - lmax[i] + 1) * (rmax[i] - i + 1) - 1);
    printf("%lld\n", res);
}

int main() {
    scanf("%d", &T);
    while (T--)
        solve();
    return 0;
}

Q 小A的柱状图

解题思路

O Largest Rectangle in a Histogram 的变式，前缀和预处理一下。

C++ 代码

#include <bits/stdc++.h>
using namespace std;
const int N = 1000010;

int n, a[N], h[N];
int l[N], r[N];
int stk[N], tt;

int main() {
    scanf("%d", &n);
    for (int i = 1; i <= n; i++)
        scanf("%d", &a[i]);
    for (int i = 1; i <= n; i++)
        a[i] += a[i - 1];
    for (int i = 1; i <= n; i++)
        scanf("%d", &h[i]);
    for (int i = 1; i <= n; i++) {
        while (tt && h[stk[tt]] >= h[i])
            tt--;
        if (tt)
            l[i] = stk[tt];
        else
            l[i] = 0;
        stk[++tt] = i;
    }
    tt = 0;
    for (int i = n; i; i--) {
        while (tt && h[stk[tt]] >= h[i])
            tt--;
            if (tt)
                r[i] = stk[tt];
            else
                r[i] = n + 1;
            stk[++tt] = i;
    }
    long long res = 0;
    for (int i = 1; i <= n; i++)
    res = max(res, 1ll * (a[r[i] - 1] - a[l[i]]) * h[i]);
    printf("%ld\n", res);
    return 0;
}

S [USACO 2012 Mar S]Flowerpot

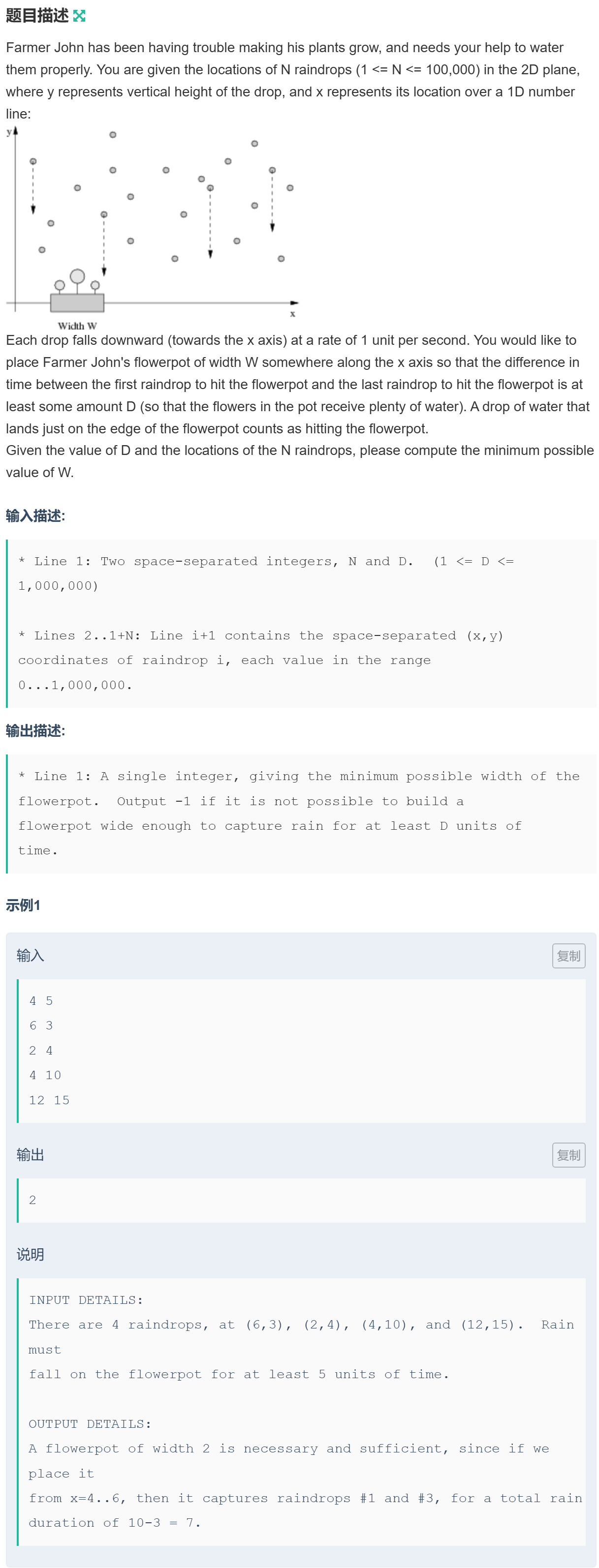
解题思路

根据题意，需要找到一个花盆的宽度 \(w\)，使得该花盆可以覆盖的雨滴，从第一个到最后一个的时差不小于 \(D\)，即雨滴的纵坐标的最大最小值之差不小于 \(D\)。
求解 \(x\) 的最小值，则考虑使用二分：每次判断当前的 \(w\) 是否满足条件。

C++ 代码

#include <bits/stdc++.h>
using namespace std;
const int N = 1000010;

int n, D, res = -1;
struct R {
    int x, y;
} r[N];

bool cmp(R a, R b) {
    return a.x <= b.x;
}

bool check(int w) {
    deque<int> qmax, qmin;
	// 维护一个 y 差值不小于 D 的区间
    for (int i = 1; i <= n; i++) {
        while (!qmin.empty() && r[qmin.back()].y >= r[i].y)
            qmin.pop_back();
        qmin.push_back(i);
        while (!qmin.empty() && r[qmin.front()].x + w < r[i].x)
            qmin.pop_front();
        while (!qmax.empty() && r[qmax.back()].y <= r[i].y)
            qmax.pop_back();
        qmax.push_back(i);
        while (!qmax.empty() && r[qmax.front()].x + w < r[i].x)
            qmax.pop_front();
        if(r[qmax.front()].y - r[qmin.front()].y >= D) 
            return true;
    }
    return false;
}

void solve() {
    sort(r + 1, r + n + 1, cmp);
    int l = 0, r = N;
    while (l < r) {
        int mid = l + r >> 1;
        if (check(mid)) {
            r = mid;
            res = mid;
        } else
            l = mid + 1;
    }
    printf("%d\n", res);
}

int main() {
    scanf("%d%d", &n, &D);
    for (int i = 1; i <= n; i++)
        scanf("%d%d", &r[i].x, &r[i].y);
    solve();
    return 0;
}