牛客刷题-Day23

牛客刷题-Day23

今日刷题：\(1041-1045\)

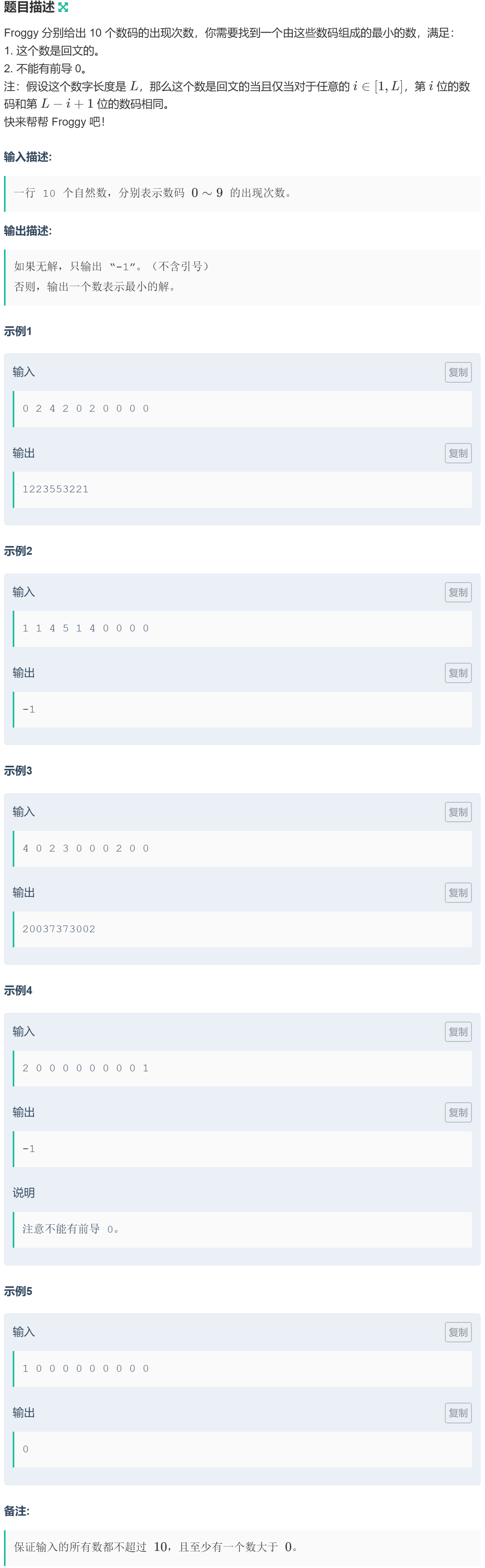
1041 习题-回文数

解题思路

构成回文数的情况：

1. 出现次数为奇数的数最多一个；
2. 在情况一的基础上，\(0\) 出现次数不为零且有出现次数至少为 \(2\) 的数，或者 \(0\) 出现次数为 \(1\) 无其余数。

当可以构成回文数，要求回文数最小，因此在不存在前导零的情况下，首位为不为零的最小数，若存在 \(0\)，则在安排完首位之后先安排 \(0\)，之后依次按照递增的顺序安排数字。

C++ 代码

#include <bits/stdc++.h>
using namespace std;
const int N = 10, M = 110;

int cnt[N];
int s[N];

int main() {
    int flag = 0, total = 0, t = -1;
    for (int i = 0; i < N; i++) {
        scanf("%d", &cnt[i]);
        if (cnt[i] % 2) {
            flag++;
            t = i;
        }
        total += cnt[i]; // 总个数
    }
    if (flag > 1) {
        printf("-1\n");
        return 0;
    }
    if (cnt[0]) {
        flag = 0;
        for (int i = 1; i < N; i++)
            if (cnt[i] > 1)
                flag = 1;
        if (!flag) {
            if (cnt[0] > 1) {
                printf("-1\n");
                return 0;
            }
        }
    }
    int idx = 1;
    for (int i = 1; i < N; i++) {
        if (cnt[i] && cnt[i] > 1) {
            while (cnt[i] > 1) {
                s[idx] = i, s[total + 1 - idx] = i;
                cnt[i] -= 2;
                idx++;
                if (cnt[0]) {
                    while (cnt[0] > 1) {
                        s[idx] = 0, s[total + 1 - idx] = 0;
                        cnt[0] -= 2;
                        idx++;
                    }
                }
            }
        }
    }
    if (t != -1)
        s[idx] = t;
    for (int i = 1; i <= total; i++)
        printf("%d", s[i]);
    return 0;
}

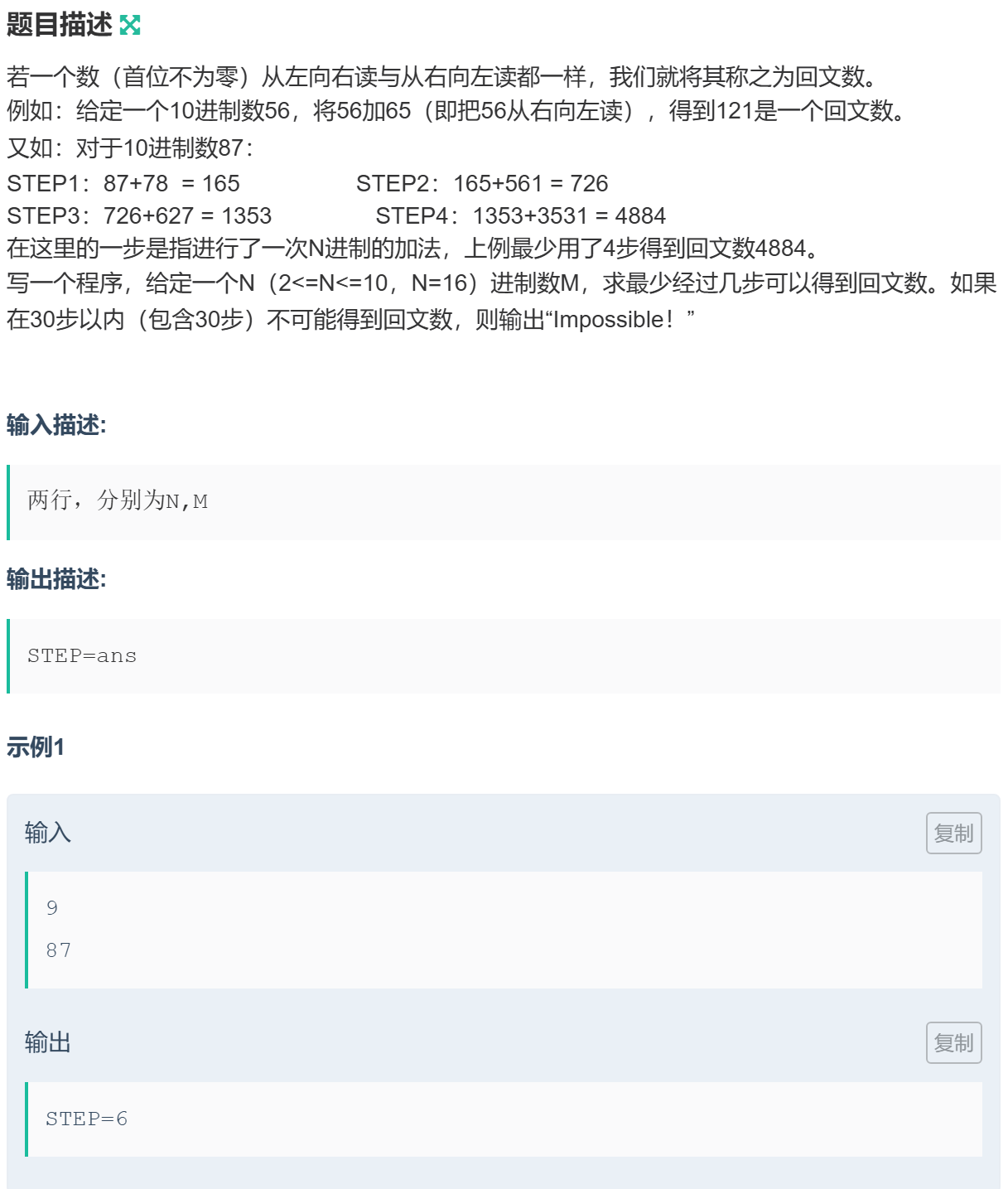
1043 习题-[NOIP1999]回文数

解题思路

牛客的题目描述不是很清晰：\(n\) 的取值为 \([2,10]\)，或者 \(n=16\)；其次输入的数字长度不超过 \(100\)。

按照题目的描述模拟加法过程，当超过 \(30\) 次之后的数仍不是回文数，则输出 Impossible!。
因为两个同样位数的数加和最多多一位，因此如果使用数组，则最多进 \(30\) 位。另外需要注意 \(16\) 进制的数会使用大写字母 \([A,F]\)。

C++ 代码

#include <bits/stdc++.h>
using namespace std;

int n;
string s;
vector<int> num;

vector<int> add(vector<int> num, int k) {
    vector<int> a = num, b, c;
    for (int i = num.size() - 1; i >= 0; i--)
        b.push_back(num[i]);
    int t = 0;
    for (int i = 0; i < num.size(); i++) {
        t += a[i] + b[i];
        c.push_back(t % k);
        t /= k;
    }
    if (t)
        c.push_back(1);
    return c;
}

int solve(vector<int> &num, int k) { // k 进制
    int cnt = 0;
    while (1) {
        bool flag = true;
        for (int i = 0, j = num.size() - 1; i <= j; i++, j--) {
            if (num[i] != num[j]) {
                flag = false;
                break;
            }
        }
        if (flag)
            return cnt;
        num = add(num, k);
        cnt++;
        if (cnt > 30)
            break;
    }
    return cnt;
}

int main() {
    cin >> n >> s;
    for (int i = s.size() - 1; i >= 0; i--) {
        if (s[i] >= '0' && s[i] <= '9') {
            num.push_back(s[i] - '0');
        } else {
            num.push_back(s[i] - 'A' + 10);
        }
    }
    int step = solve(num, n);
    if (step <= 30) {
        printf("STEP=%d\n", step);
        return 0;
    }
    puts("Impossible!");
    return 0;
}

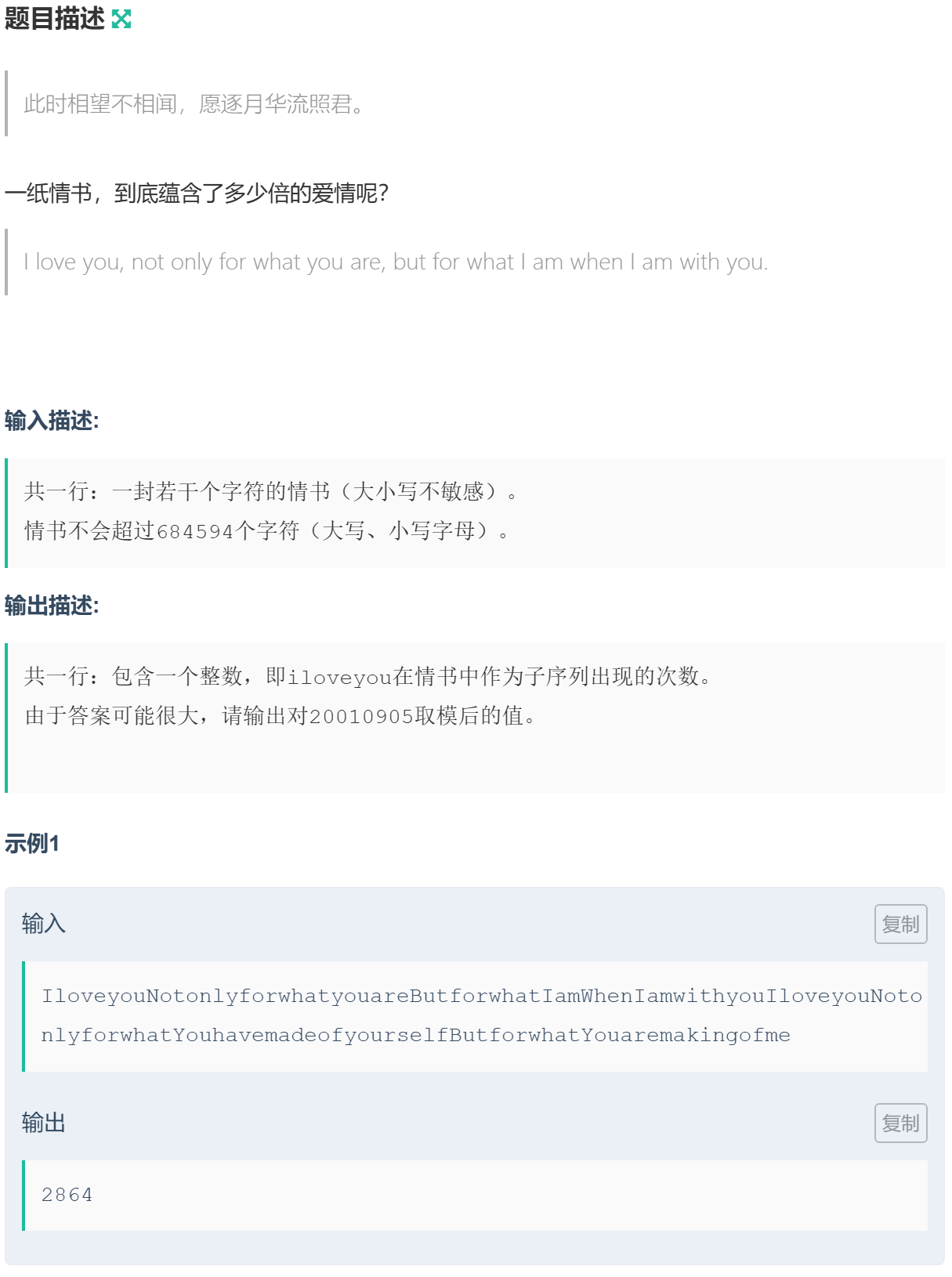
1045 习题-I love you

解题思路

\(f_{i,j}\) 表示 \(t[0-j-1]\) 在 \(s[0-i-1]\) 的匹配个数，状态计算如下：

• 初始化：\(f_{0,0}=1\)，空序列匹配。
• 若 \(s_{i-1}==t_{j-1}\)，则 \(f_{i,j}+=f_{i,j}\)。

在实现时对数组进行降维。

C++ 代码

#include <bits/stdc++.h>
using namespace std;
const int N = 10;

string s;
int f[N];

int main() {
    f[0] = 1;
    getline(cin, s);
    string t = "iloveyou";
    for (int i = 0; s[i]; i++) {
        bool flag = true;
        for (int j = 0; t[j]; j++)
            if (s[i] == t[j] || s[i] - 'A' + 'a' == t[j]) {
                f[j + 1] = (f[j + 1] + f[j]) % 20010905;
            }
    }
    printf("%d\n", f[8]);
    return 0;
}