牛客刷题-Day19
牛客刷题-Day19
今日刷题:\(1011-1020\)
1011 枚举 · 例9-中位数图

解题思路
前缀和。对原排列进行处理,大于 \(b\) 为 \(-1\),小于 \(b\) 为 \(1\)。从 \(b\) 所在索引往左(右)枚举,当前和为 \(0\),则说明左(右)侧大于和小于 \(b\) 的数的个数相等,此时为一个符合要求的序列。
另一种,往左侧枚举时,记录当前和 \(sum\) 的个数;在往右侧枚举时,取 \(-sum\) 加入答案中。比如往右侧枚举时,\(sum\) 为正数(零、负数),说明此时右侧的大于 \(b\) 的数比小于 \(b\) 的数多(一样、少) \(sum\) 个。这样两边分别取数,也是可以构成符合要求的序列。
C++ 代码
#include <bits/stdc++.h>
using namespace std;
const int N = 100010;
int n, b, a[N];
int s[N];
map<int, int> cnt;
int main() {
scanf("%d%d", &n, &b);
int idx = 0;
for (int i = 1; i <= n; i++) {
scanf("%d", &a[i]);
if (a[i] < b) {
s[i] = -1;
} else if (a[i] > b) {
s[i] = 1;
} else {
s[i] = 0;
idx = i;
}
}
int sum = 0, res = 1;
for (int i = idx - 1; i; i--) {
sum += s[i];
cnt[sum]++;
if (sum == 0)
res++;
}
sum = 0;
for (int i = idx + 1; i <= n; i++) {
sum += s[i];
if (sum == 0)
res++;
res += cnt[-sum];
}
printf("%d\n", res);
return 0;
}
1013 枚举 · 例11-带权中位数
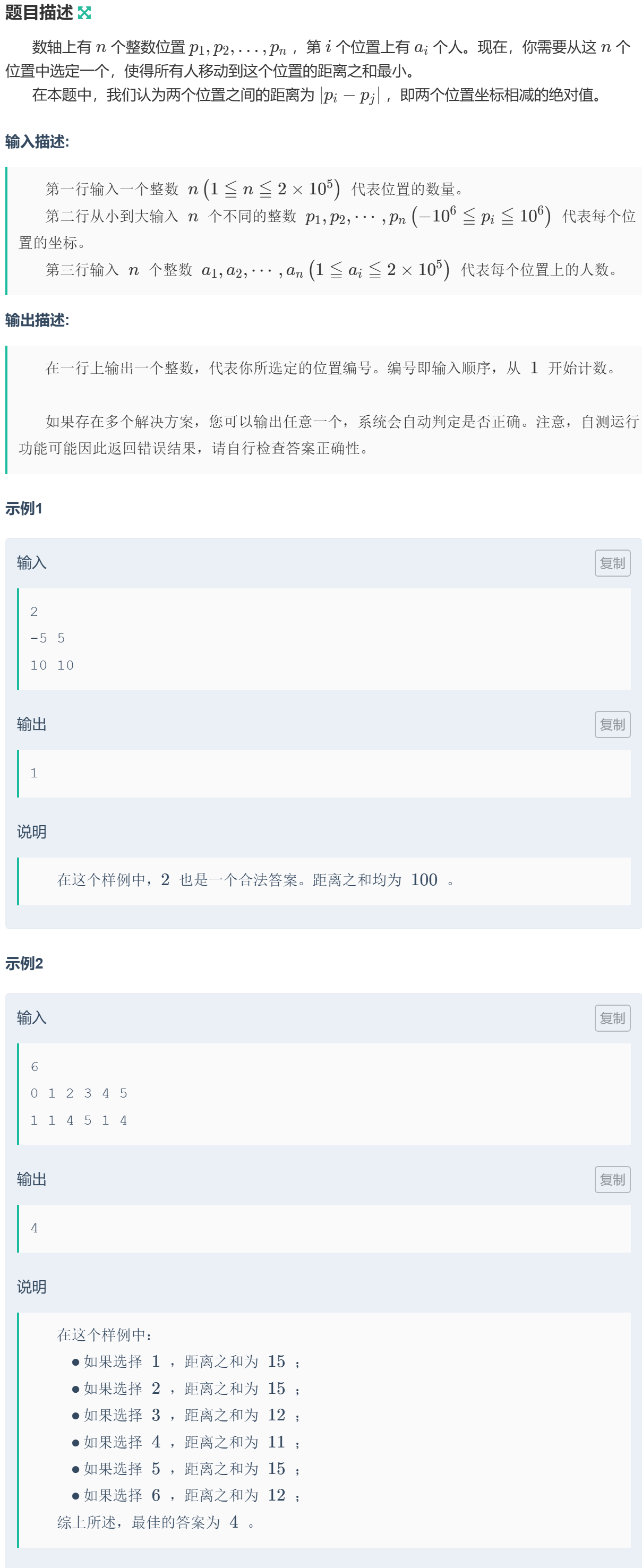
解题思路
相关结论参考:[总结]中位数及带权中位数问题
C++ 代码
#include <bits/stdc++.h>
using namespace std;
const int N = 2e5 + 10;
int n, a[N];
int main() {
scanf("%d", &n);
long long sum = 0, cnt = 0;
for (int i = 1; i <= n; i++) {
int p;
scanf("%d", &p);
}
for (int i = 1; i <= n; i++) {
scanf("%d", &a[i]);
sum += a[i];
}
for (int i = 1; i <= n; i++) {
cnt += a[i];
if (cnt * 2 >= sum) {
cout << i << endl;
break;
}
}
return 0;
}
1015 枚举 · 例14-最短合法子串

解题思路
双指针。当满足子序列中存在所有小写字母时右指针停止移动,左指针开始移动,只要满足子序列中存在所有小写字母,就更新答案并移动左指针,在移动之前去除相关字母。
C++ 代码
#include <bits/stdc++.h>
using namespace std;
string s;
map<char, int> cnt;
bool check() {
if (cnt.size() < 26)
return false;
for (auto [k, v]: cnt) {
if (v == 0)
return false;
}
return true;
}
int main() {
cin >> s;
int res = s.size() + 1;
for (int i = 0, j = 0; s[i]; i++) {
if (cnt.find(s[i]) == cnt.end())
cnt[s[i]] = 1;
else
cnt[s[i]]++;
while (check()) {
res = min(res, i - j + 1);
if (cnt[s[j]])
cnt[s[j]]--;
j++;
}
}
if (res == s.size() + 1)
res = -1;
cout << res << endl;
return 0;
}
1016 枚举 · 例15-丢手绢

解题思路
双指针。首先记录总的距离和 \(sum\),那么一个点到另一个点的顺时针距离为 \(a\),则逆时针距离为 \(b=sum-a\)。则这两个点之间的距离为 \(min\{a,sum-a\}\)。\(t\) 记录 \(j\) 到 \(i\) 的顺时针距离。
C++ 代码
#include <bits/stdc++.h>
using namespace std;
const int N = 100010;
typedef long long LL;
int n;
LL a[N];
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; i++)
scanf("%lld", &a[i]);
LL sum = 0, ans = 0;
for (int i = 1; i <= n; i++)
sum += a[i];
LL t = 0;
for (int i = 1, j = 1; i <= n; i++) {
t += a[i];
while (2 * t >= sum) {
ans = max(ans, sum - t);
t -= a[j++];
}
ans = max(ans, t);
}
printf("%lld\n", ans);
return 0;
}
1017 枚举 · 例16-迷你扫雷
解题思路
递推。\(a_i\) 表示第一列的地雷数量,\(b_i\) 表示 \(a_{i-1}\) 到 \(a_{i+1}\) 的地雷数的和。从 \(a_1=\{0/1\}\) 开始,\(a_0\) 为 \(0\),那么:
| 第一列 | 计算 |
|---|---|
| \(a_2\) | \(b_1-a_1-a_0\) |
| \(a_3\) | \(b_2-a_2-a_1\) |
| \(...\) | \(...\) |
| \(a_n\) | \(b_{n-1}-a_{n-1}-a_{n-2}\) |
由此,当 \(a_1\) 固定时,后面的 \(a_i\) 都是固定的,都可以通过同样的公式推导得到。而 \(a_1\) 只有 \(0\) 或者 \(1\) 两种取值,因此只需要判断这两种情况递推得到的 \(a\) 序列是否合法即可,首先 \(a_i\) 只能是 \(0\) 或者 \(1\),其次,当我们计算完 \(a_n\) 之后,计算一下 \(b_n-a_n-a_{n-1}\) 是否为 \(0\),因为合法方案该值应该为 \(0\)。
C++ 代码
#include <bits/stdc++.h>
using namespace std;
const int N = 10010;
int n;
int a[N], b[N];
bool check1() {
a[1] = 0;
for (int i = 2; i <= n; i++) {
a[i] = b[i - 1] - a[i - 2] - a[i - 1];
if (a[i] < 0 || a[i] > 1) return false;
}
a[n + 1] = b[n] - a[n - 1] - a[n];
if (a[n + 1])
return false;
return true;
}
bool check2() {
a[1] = 1;
for (int i = 2; i <= n; i++) {
a[i] = b[i - 1] - a[i - 2] - a[i - 1];
if (a[i] < 0 || a[i] > 1) return false;
}
a[n + 1] = b[n] - a[n - 1] - a[n];
if (a[n + 1])
return false;
return true;
}
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; i++)
scanf("%d", &b[i]);
printf("%d\n", check1() + check2());
return 0;
}
枚举 · 例17扩展-翻转游戏:hard
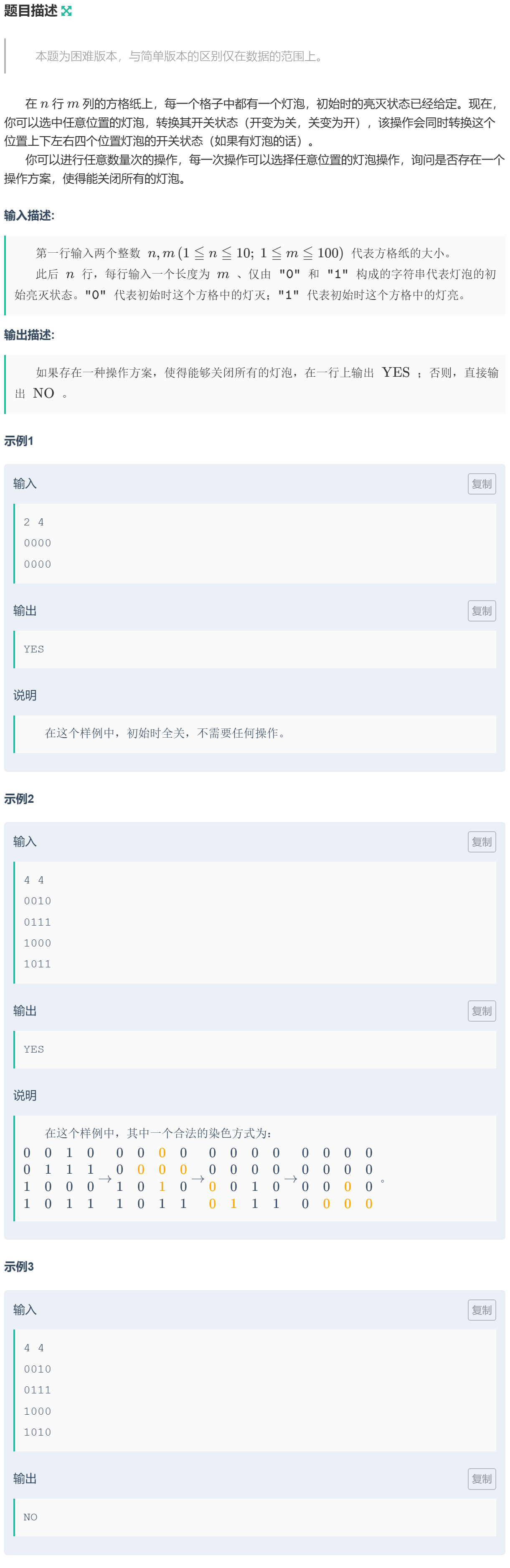
解题思路
递推。这里按照列进行操作以确保时间,时间复杂度为 \(O(2^n\times n\times m)\)。
对于第一列,可以操作的方案共 \(2^n\) 种,乘法原理得到。当第一列操作固定之后,之后的操作都依赖于第一列的操作结果。如果上一列存在未关闭的灯,则进行关灯操作。最后判断最后一列是否存在未关闭的灯。
C++ 代码
#include <bits/stdc++.h>
using namespace std;
const int N = 20, M = 110;
int dx[] = {-1, 0, 1, 0, 0}, dy[] = {0, -1, 0, 1, 0};
int n, m;
char s[N][N], backup[N][N];
void turn(int x, int y) {
for (int i = 0; i < 5; i++) {
int a = x + dx[i], b = y + dy[i];
if (a < 0 || a >= n || b < 0 || b >= m)
continue;
s[a][b] ^= 1;
}
}
int main() {
scanf("%d%d", &n, &m);
for (int i = 0; i < n; i++)
scanf("%s", s[i]);
for (int op = 0; op < 1 << n; op++) {
memcpy(backup, s, sizeof s);
for (int i = 0; i < n; i++) // 操作第一列
if ((op >> i) & 1)
turn(i, 0);
for (int j = 1; j < m; j++)
for (int i = 0; i < n; i++)
if (s[i][j - 1] == '1') {
turn(i, j);
}
bool flag = false;
for (int i = 0; i < n; i++)
if (s[i][m - 1] == '1')
flag = true;
if (!flag) {
puts("YES");
return 0;
}
memcpy(s, backup, sizeof s);
}
puts("NO");
return 0;
}
1020 枚举 · 例18-最大的半径

解题思路
枚举。这里我们使用 \(bitset\) 进行优化。
枚举两个点 \(a\) 和 \(b\),则二者之间的距离为 \(len(a,b)\),需要寻找是否存在 \(c\) 使得 \(c\) 到 \(a\) 和 \(b\) 的距离都要不小于 \(len(a,b)\)。
那么如何寻找 \(c\) 呢?首先预处理任意两个点之间的距离,然后对于该序列,按照距离的递减排序,那么枚举到的边都存储一次,如果 \(a\) 和 \(b\) 的邻接点存在公共点,则该点的就是符合要求的 \(c\)。具体如下:
// 邻接表声明
bitset<N> st[N];
// 存储邻接点
st[a][b] = st[b][a] = 1;
// 是否存在公共点,即 st[a] & st[b] 中 “1” 的个数是否为零
int cnt = (st[a] & st[b]).count();
C++ 代码
#include <bits/stdc++.h>
using namespace std;
const int N = 3010;
int n, m;
int x[N], y[N];
bitset<N> st[N];
struct Node {
int a, b;
double dist;
} a[N * N / 2];
double len(int a, int b) {
return sqrt((x[a] - x[b]) * (x[a] - x[b]) + (y[a] - y[b]) * (y[a] - y[b]));
}
bool cmp(Node a, Node b) {
return a.dist > b.dist;
}
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; i++)
scanf("%d%d", &x[i], &y[i]);
for (int i = 1; i <= n; i++)
for (int j = i + 1; j <= n; j++)
a[++m] = {i, j, len(i, j)};
sort(a + 1, a + m + 1, cmp);
for (int i = 1; i <= m; i++) {
int c = a[i].a, d = a[i].b;
double l = a[i].dist;
st[c][d] = st[d][c] = 1;
if ((st[c] & st[d]).count()) {
printf("%lf\n", l / 2);
return 0;
}
}
return 0;
}
本文来自博客园,作者:Cocoicobird,转载请注明原文链接:https://www.cnblogs.com/Cocoicobird/p/19176846

 浙公网安备 33010602011771号
浙公网安备 33010602011771号