牛客刷题-Day2

牛客刷题-Day2

今日题目：\(1006-1010\)

1006 免费馅饼

题目描述

\(SERKOI\) 最新推出了一种叫做“免费馅饼”的游戏：游戏在一个舞台上进行。舞台的宽度为 \(W\) 格，天幕的高度为 \(H\) 格，游戏者占一格。开始时游戏者站在舞台的正中央，手里拿着一个托盘。
游戏开始后，从舞台天幕顶端的格子中不断出现馅饼并垂直下落。游戏者左右移动去接馅饼。游戏者每秒可以向左或向右移动一格或两格，也可以站在原地不动。
馅饼有很多种，游戏者事先根据自己的口味，对各种馅饼依次打了分。同时，在 \(8-308\) 电脑的遥控下，各种馅饼下落的速度也是不一样的，下落速度以格/秒为单位。
当馅饼在某一秒末恰好到达游戏者所在的格子中，游戏者就收集到了这块馅饼。
写一个程序，帮助我们的游戏者收集馅饼，使得所收集馅饼的分数之和最大。

输入描述

第一行是用空格隔开的两个正整数，分别给出了舞台的宽度 \(W\)（\(1\) 到 \(99\) 之间的奇数）和高度 \(H\)（\(1\) 到 \(100\) 之间的整数）。
接下来依馅饼的初始下落时间顺序给出了所有馅饼的信息。每一行给出了一块馅饼的信息。由四个正整数组成，分别表示了馅饼的初始下落时刻（\(0\) 到 \(1000\) 秒），水平位置、下落速度（\(1\) 到 \(100\)）以及分值。游戏开始时刻为 \(0\)。从 \(1\) 开始自左向右依次对水平方向的每格编号。
输入文件中同一行相邻两项之间用一个或多个空格隔开。

输出描述

第一行给出了一个正整数，表示你的程序所收集的最大分数之和。
其后的每一行依时间顺序给出了游戏者每秒的决策。输出 \(0\) 表示原地不动、\(1\) 或 \(2\) 表示向右移动一步或两步、\(-1\) 或 \(-2\) 表示向左移动一步或两步。输出应持续到游戏者收集完他要收集的最后一块馅饼为止。

示例

输入

3 3
0 1 2 5 
0 2 1 3
1 2 1 3
1 3 1 4

输出

12
-1
1
1

解题思路

• 状态表示：\(f_{i,j}\) 表示 \(i\) 时刻位于 \(j\) 处的分数，求解最大值。
• 状态计算：对于转移 \(k\in[-2,2],k\in Z\) 个单位，则 \(i+1\) 时刻，\(f_{i+1,j+k}=f_{i,j}+score_{i + 1,j + k}\)。

C++ 代码

#include <bits/stdc++.h>
using namespace std;
const int N = 110, M = 1010;
typedef long long LL;

int W, H, n;
LL f[M][N];
LL score[M][N];
int path[M][N];

int main() {
    cin >> W >> H;
    int st = (W + 1) / 2;
    H--;
    int t, col, sp, val;
    while (cin >> t >> col >> sp >> val) {
        if (H % sp == 0) {
            t = t + H / sp;
            score[t][col] += (LL) val;
            n = max(n, t);
        }
    }
    memset(f, -1, sizeof f);
    f[0][st] = score[0][st];
    for (int i = 0; i <= n; i++) {
        for (int j = 1; j <= W; j++) {
            for (int k = -2; k <= 2; k++) {
                if (f[i][j] == -1) continue;
                if ((j + k) >= 1 && (j + k) <= W) {
                    LL cnt = f[i][j] + score[i + 1][j + k];
                    if (cnt > f[i + 1][j + k]) {
                        f[i + 1][j + k] = cnt;
                        path[i + 1][j + k] = k;
                    }
                }
            }
        }
    }
    t = 0, col = st; 
    LL ans = 0;
    for (int i = 0; i <= n; i++)
        for (int j = 1; j <= W; j++) {
            if (f[i][j] > ans) {
                t = i, col = j;
                ans = f[i][j];
            }
        }
    cout << ans << endl;
    stack<int> stk;
    for (int i = t; i >= 1; i--) {
        stk.push(path[i][col]);
        col -= path[i][col];
    }
    while (!stk.empty()) {
        cout << stk.top() << endl;
        stk.pop();
    }
    return 0;
}

1007 钉子和小球

题目描述

有一个三角形木板,竖直立放，上面钉着 \(\frac{n(n+1)}{2}\) 颗钉子，还有 \(n+1\) 个格子（当 \(n=5\) 时如图 \(1\)）。每颗钉子和周围的钉子的距离都等于d，每个格子的宽度也都等于d，且除了最左端和最右端的格子外每个格子都正对着最下面一排钉子的间隙。

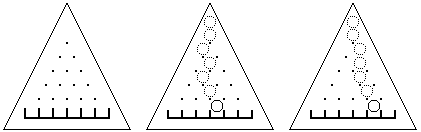
让一个直径略小于 \(d\) 的小球中心正对着最上面的钉子在板上自由滚落，小球每碰到一个钉子都可能落向左边或右边（概率各 \(\frac{1}{2}\)），且球的中心还会正对着下一颗将要碰上的钉子。例如图 \(2\) 就是小球一条可能的路径。
我们知道小球落在第 \(i\) 个格子中的概率 \(p_i=\frac{C_n^i}{2^n}\)，其中 \(i\) 为格子的编号，从左至右依次为 \(0,1,...,n\)。
现在的问题是计算拔掉某些钉子后，小球落在编号为 \(m\) 的格子中的概率 \(p_m\)。假定最下面一排钉子不会被拔掉。例如图3是某些钉子被拔掉后小球一条可能的路径。

输入描述

第 \(1\) 行为整数 \(n\)（\(2 ≤ n ≤ 50\)）和 \(m\)（\(0 ≤ m ≤ n\)）。以下 \(n\) 行依次为木板上从上至下 \(n\) 行钉子的信息，每行中 * 表示钉子还在，. 表示钉子被拔去，注意在这 \(n\) 行中空格符可能出现在任何位置。

输出描述

仅一行，是一个既约分数（\(0\) 写成 \(0/1\)），为小球落在编号为 \(m\) 的格子中的概 \(p_m\)。既约分数的定义：\(A/B\) 是既约分数，当且仅当 \(A\)、\(B\) 为正整数且 \(A\) 和 \(B\) 没有大于 \(1\) 的公因子。

示例

输入

5 2
    *
   * .
  * * *
 * . * *
* * * * *

输出

7/16

解题思路

• 状态表示：\(f_{i,j}\) 表示落在第 \(i\) 层 \(j\) 个钉子的概率。
• 状态计算：如果当前 \((i,j)\) 处是钉子，则有两种选择掉到 \((i+1,j)\) 和 \((i+1,j+1)\) 处；如果不是钉子，则直接穿下去到 \((i+2,j+1)\) 处。
  这里表示的时候选择用 pair，避免浮点数精度问题。

C++ 代码

#include <bits/stdc++.h>
using namespace std;
const int N = 55;
typedef long long LL;
#define x first
#define y second

int n, m;
char g[N][N];
pair<LL, LL> f[N][N];

LL gcd(LL a, LL b) {
    if (a % b == 0)
        return b;
    return gcd(b, a % b);
}

pair<LL, LL> add(pair<LL, LL> a, pair<LL, LL> b) {
    LL x1 = a.x, y1 = a.y == 0 ? 1 : a.y;
    LL x2 = b.x, y2 = b.y == 0 ? 1 : b.y;
    pair<LL, LL> c;
    LL d = gcd(y1, y2);
    c.y = y1 / d * y2, c.x = c.y / y1 * x1 + c.y / y2 * x2;
    return c;
}

int main() {
    cin >> n >> m;
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= i; j++)
            cin >> g[i][j];
    f[1][1].x = 1, f[1][1].y = 1;
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= i; j++) {
            LL x = f[i][j].x, y = f[i][j].y;
            if (g[i][j] == '*') {
                f[i + 1][j] = add(f[i + 1][j], make_pair(x, y * 2));
                f[i + 1][j + 1] = add(f[i + 1][j + 1], make_pair(x, y * 2));
            } else {
                f[i + 2][j + 1] = add(f[i + 2][j + 1], f[i][j]);
            }
        }
    }
    LL d = gcd(f[n + 1][m + 1].x, f[n + 1][m + 1].y);
    cout << f[n + 1][m + 1].x / d << '/' << f[n + 1][m + 1].y / d << endl;
    return 0;
}