人工智能原理及应用-搜索技术

搜索技术

知识无法精确描述，也无法通过经验来求解，即不良结构或非结构化问题；只能在状态空间中一步步摸索前进，搜索答案（目标）——搜索技术

通过对状态空间的搜索而求解问题的技术

1 搜索与问题求解

1.1 什么样的问题可以使用全局搜索技术求解

问题可以被形式化定义为四个组成部分：

• 智能体的初始状态，即搜索的开始

• 后继函数

  • 智能体采取的可能行动的描述，通常为 <行动，后继状态>
  • 初始状态和后继函数隐含地定义了问题的状态空间，状态空间中的一条路径是通过行动序列连接起来的一个状态序列；

• 目标测试——检查给定的状态是不是目标

• 路径代价函数——每条路径都有一个数值化的代价值，反映了性能度量 / 求解问题的代价

问题的解：初始状态到目标状态的路径，解的优劣由路径耗散函数量度（代价）

1.2 搜索过程的一般步骤——图搜索算法（基本思路、框架）

盲目搜索技术、启发式搜索技术是图搜索策略的细化（具体化）

1.2.1 一些基本概念

• 扩展一个节点：生成出该节点的所有后继节点，并给出它们之间的代价。这一过程称为“扩展一个节点”
• OPEN 表：存放待扩展的节点
• CLOSED 表：存放已扩展的节点

1.2.2 图搜索的一般过程

1. 建立一个只含有起始节点 S 的搜索图 G ，把 S 放到一个叫做 OPEN 的未扩展节点表中
2. 建立一个叫做 CLOSED 的已扩展节点表，其初始为空表；
3. LOOP：若 OPEN 表是空表，则失败退出
   1. 选择 OPEN 表上的第一个节点，把它从 OPEN 表移出，并放进 CLOSED 表中。记这一个节点为节点 n
   2. 若 n 为目标节点，则有解，并成功退出，所求的解是 G 中沿着指针从 n 到 S 这条路径
   3. 否则，扩展节点 n ，生成不是 n 祖先的那些后继节点的集合 M（防止出现死循环）。把 M 的成员作为 n 的后继节点加到图 G 中
   4. 对既不在 OPEN 表中又不在 CLOSED 表中的 M 成员设置一个通向 n 的指针，并加进 OPEN 表；对已经在 OPEN 或 CLOSED 中的 M 的成员，确定是否需要更改通到父节点 n 的指针方向
   5. 按某一任意方式或按某个评价函数，重排 OPEN 表（这由后面介绍的不同搜索技术决定）
   6. GO LOOP

解是在搜索树 G 中反向追踪从目标节点到起始节点的指针的一条路径。当 OPEN 表为空，则问题无解

e 中对 OPEN 表中节点进行排序，目的是选出一个“最好”的节点作为下一步扩展的节点。不同的排序原则对应于不同的具体算法：

• 盲目搜索技术：人为排序原则
• 启发式搜索技术：依据估价函数的值

2 无信息搜索策略

2.1 广度优先搜索

OPEN 表：已经生成出来但其子状态未被搜索的状态，广度优先搜索中采用先进先出队列FIFO

CLOSED 表：记录了已被生成扩展过的状态

广度优先搜索中每个结点的搜索次序类似树的层序遍历顺序

从 4 个度量来评价广度优先搜索，假设最浅目标节点的深度为 d，每个节点有 b 个后继，状态空间的最大深度为 \(m\)

• 完备性：总能找到一个解
• 最优性：如果每步扩展消耗相同，广度优先搜索能找到最优解
• 指数级的时间消耗：\(1+b+b^2+...+b^d=O(b^{d+1})\)
• 内存消耗是比执行时间消耗更大的问题：\(O(b^{d+1})\)

2.2 深度优先 / （迭代）深度有限搜索

OPEN表：是后进先出队列LIFO

内存需求小，为 \(O(bm)\)，不是完备和最优的，最坏的时间复杂度为 \(O(b^m)\)

为什么空间复杂度为 \(O(bm)\)？

搜索流程如下：

1. Push 1, 2, 3, ..., b
2. Pop 1, Push 11, 12, 13, ..., 1b
3. Pop 11, Push 111, 112, 113, ..., 11b
4. ...
5. Pop \(1^{m-1}\), Push \(1^{m-1}1\), \(1^{m-1}2\), ..., \(1^{m-1}b\)

此时，栈中含有 \(1^{m-1}1\)、\(1^{m-1}2\)、...、\(1^{m-1}b\)、...、112、...、11b、12、...、1b、2、...、b，共计 \((b-1)m+1\) 个结点

2.2.1 深度有限搜索

深度优先搜索的无边界问题可以通过提供一个预先设定的深度限制 \(l\) 来解决

深度 \(l\) 的节点当作无后继节点看待，虽然解决了无限路径问题，但如果 \(l<d\) 则找不到解

时间复杂度为 \(O(b^{l})\)，空间复杂度为 \(O(bl)\)

2.2.2 迭代深度有限搜索

每次改变限制深度，多次调用深度有限搜索算法，就得到了叠代深入深度优先搜索算法

结合了广度优先和深度优先两种算法的优点：分支因子有限时是完备的 / 路径代价是节点深度的非递增函数时是最优的

时间复杂度分析：深度由 \(1\) 迭代到 \(d\)，每次迭代都要遍历一次树，则每层节点（从 \(0\) 到 \(d\)）被遍历的次数从 \(d\) 依次递减，因此 \(d*1+(d-1)*b+...+1*b^{d}=O(b^d)\)

空间复杂度分析：\(O(bd)\)

2.3 无信息搜索策略对比

评价标准	广度优先	深度优先	深度有限	迭代深入	双向搜索
完备性	是 A	否	否	是 A	是 A / D
时间复杂度	\(O(b^{d+1})\)	\(O(b^m)\)	\(O(b^l)\)	\(O(b^d)\)	\(O(b^{\frac{d}{2}})\)
空间复杂度	\(O(b^{d+1})\)	\(O(bm)\)	\(O(bl)\)	\(O(b^d)\)	\(O(b^{\frac{d}{2}})\)
最优性	是 C	否	否	是 C	是 C / D

关于 A / B / C / D的解释：A—如果 \(b\)有限则是完备的 / B—单步耗散 \(≥e\) 则是完备的 / C—如果单步耗散都是相同的则是最优的 / D—两个方向上都使用广度优先搜索

3 启发式搜索策略

盲目搜索的不足：效率低，耗费过多的计算空间与时间，因为待扩展的节点顺序固定，系统不会对有希望达到目标的节点特别关照

启发式搜索（有信息搜索）：利用相关领域特征的启发信息来排列待扩展节点的顺序，从而选择“最有希望”的节点作为下一个被扩展的节点，这种搜索策略称之为启发式搜索

3.1 启发式搜索策略基本思想

• 假定有一个估值函数 \(f(n)\)，可以帮助确定下一个要扩展的最优节点。把当前新状态按估计值从小到大的顺序插入 OPEN 表中

• 估值函数 \(f\) 需要与当前状态到目标状态的距离相关，否则将变回盲目搜索

  • \(f\) = 状态节点的深度（无附加信息），则为广度优先搜索

  • \(f\) = 状态节点的深度的负数（无附加信息），则为深度优先搜索

贪婪最佳优先搜索 / A* 搜索（A* 算法）

3.2 贪婪最佳优先搜索

贪婪最佳优先搜索的评价函数 \(f(n)=h(n)\)

\(h(n)\)——从节点 n 到目标节点的最低代价的估计值

举例：罗马尼亚公路问题中，采用的启发函数定义为当前状态到目标的直线距离，但是在该问题中，贪婪算法可能会陷入死循环，不具备完备性

3.3 A* 搜索

基本思路：避免扩展耗散值已经很大的路径

评价函数：\(f(n)=h(n)+g(n)\)

• \(g(n)\)：从初始节点到该节点 n 的路径耗散
• \(h(n)\)：从节点 n 到目标节点的最低代价的估计值（和上文的定义一样），称为启发式或启发函数
• \(f(n)\) = 经过节点 n、具有最低代价的解的估计代价值（所有评价函数代价的下限）

---

A* 算法的性能取决于启发函数 \(h(n)\)，若启发函数 \(h(n)\) 满足一定条件，则 A* 搜索是完备的和最优的

如果 \(h(n)\) 是可采纳的，那么使用 Tree-Search 的 A* 算法是最优的，启发函数 \(h(n)\) 是可采纳的——\(h(n)\) 满足 \(h(n) ≤ h^*(n)\)

证明：假设某次优目标节点 \(G_2\) 已经产生并且在 Fringe 表中排队，设 n 是 Fringe 表中到达最优节点 \(G\) 的最短路径上的一个未扩展节点

① \(f(G_2)=g(G_2)\)

② \(f(G)=g(G)\)

③ \(g(G_2)>g(G)\)

④ \(f(G_2)>f(G)\)

⑤ \(h(n)\le h^*(n)\), \(g(n)+h(n)\le g(n)+h^*(n)\)

⑥ \(f(n) \le f(G)\)

⑦ \(f(G_2) \ge f(n)\)

因此，算法不会在选择 n 节点之前选择 \(G_2\) 进行扩展

\(h^*(n)\) 是从当前节点 n 到达目标的最低真实代价，即 \(f(n)\) 永远不会高估经过节点 n 的解的实际代价——\(f(n)≤f^*(n)\)，所以是最优解

如果启发函数大于这个上限 \(h^*(n)\)，则搜索算法出现发散，不能保证总能找到最优解

---

如果要求不以指数级增长，则启发函数需要满足

\[|h(n)-h^*(n)|\le O(log(h^*(n))) \]

即启发函数 \(h(n)\) 代表了算法采用的启发信息量

如果令 \(f(n) = g(n) + 0\)，此时启发为 \(0\)，退化为盲目搜索，必定能找到最优解，但效率最低

如果添加“一点点”启发，搜索效率提高并仍然能找到最优解

启发函数不能高于 \(h^*(n)\)，但是要尽量接近 \(h^*(n)\)

---

A* 搜索的关键如何找到是一个合适的启发函数，寻找策略：

• 从松弛问题中获得——松弛问题的最优解的耗散是原问题的一个可采纳的启发函数
• 从给定问题子问题的解耗散中获得——建立模式数据库，存储每个可能子问题实例
• 从经验中学习——使用归纳学习算法，使用相关状态特征来预测

4 博弈搜索

在竞争的环境中，每个智能体的目的是冲突的，由此引出对抗搜索问题—称为博弈。从智能体角度看，博弈是多智能体之间的竞争和对抗

本部分讨论两人对决、确定的、全局可观察的、竞争对手轮流行动、零和游戏的博弈

---

井字棋博弈树

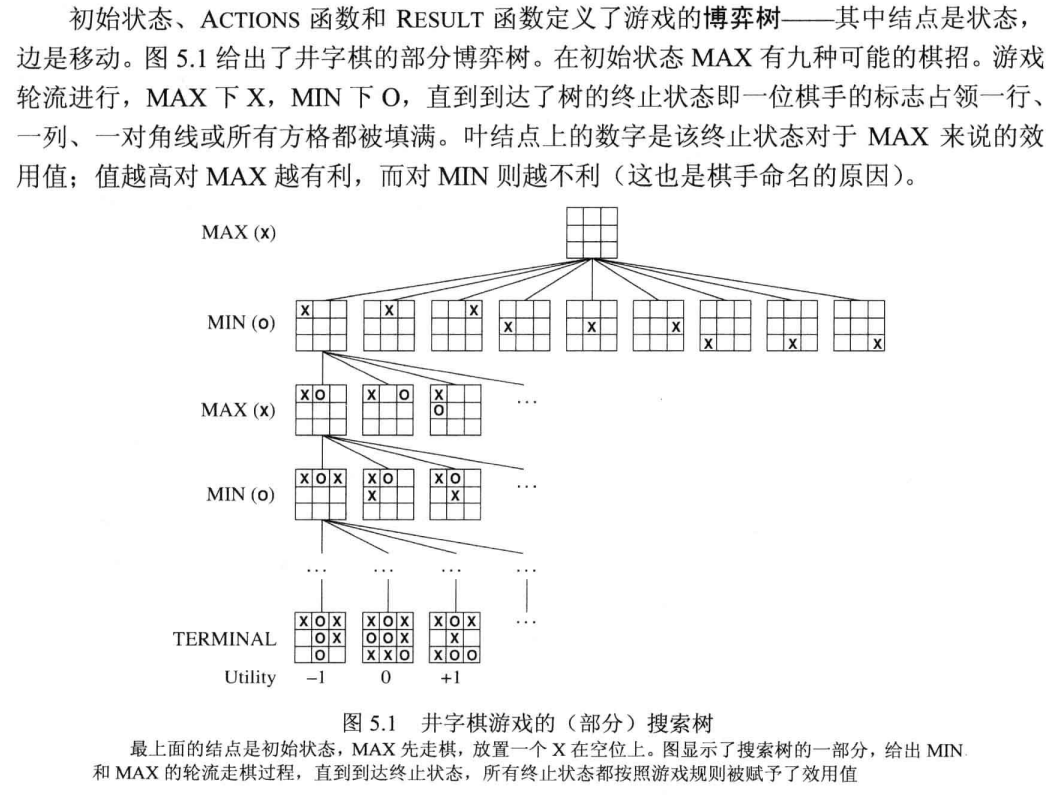
主要探讨两个问题——如何搜索到取胜的路径 / 如何提高搜索效率

相应的方法——最优策略（极大极小决策）/ \(\alpha-\beta\) 剪枝

4.1 极大极小策略

给定一颗博弈树，最优策略可以通过检查每个节点的极大极小值来决定，记为 \(MAX-MIN(n)\)。假设两个游戏者始终按照最优策略行棋，那么节点的极大极小值就是对应状态的效用值（对于 \(MAX\) 而言）。显然，终止状态的极大极小值就是它的效用值自身。更一步，对于给定的选择，\(MAX\) 喜欢移动到有极大值的状态，而 \(MIN\) 喜欢移动到有极小值的状态，所以有下面的公式：

\[MAX-MIN(n)=\begin{cases} Utility(n) \qquad 当\ n\ 为终止状态\\ max_{s\in son(n)}MAX-MIN(s)\qquad 当\ n\ 为\ MAX \ 节点\\ min_{s\in son(n)}MAX-MIN(s)\qquad 当\ n\ 为\ MIN \ 节点 \end{cases} \]

\(MAX\) 取其后继节点中最大者，\(MIN\) 取其后继节点中最小者

该算法执行深度优先搜索，假设树的深度为 \(m\)，每个节点的合法行棋有 \(b\) 个，则时间复杂度为 \(O(b^m)\)，一次性生成所有后继节点空间复杂度为 \(O(bm)\)，每次生成一个后继节点空间复杂度为 \(O(m)\)

4.2 \(\alpha-\beta\) 剪枝

通过剪枝可以忽略一些分支，这些分支不影响算法结果

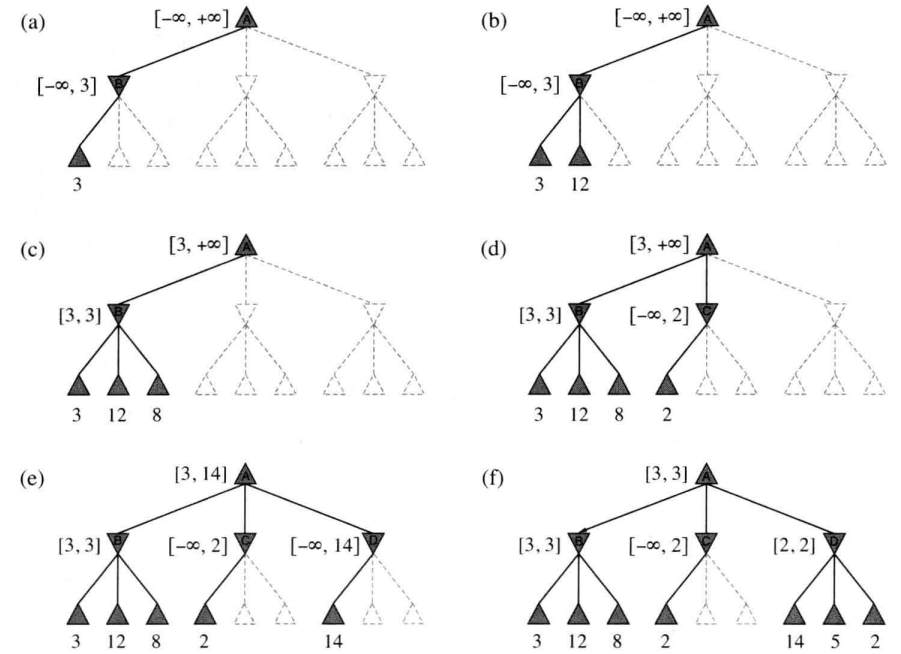
\(a\). \(B\) 下第一个叶节点的值为 \(3\)，此时作为 \(MIN\) 层的节点 \(B\) 的值最多为 \(3\)

\(b\). \(B\) 的第二个叶节点的值为 \(12\)，\(MIN\) 不会采取该行动，此时 \(B\) 的值仍然至多为 \(3\)

\(c\). \(B\) 的第三个叶节点的值为 \(8\)；此时 \(B\) 的所有后继已经遍历，\(B\) 的值即为 \(3\)

\(d\). \(C\) 的第一个叶节点的值为 \(2\)，所以 \(C\) 的值至多为 \(2\)，但是已经知道 \(B\) 的值为 \(3\)，因此 \(MAX\) 不会选择 \(C\)，此时 \(C\) 的其它后继就不会考虑了（这里就是 \(\alpha-\beta\) 剪枝的实例）

\(e\). \(D\) 的第一个叶节点的值为 \(14\)，此时 \(D\) 的 \(MIN\) 至多为 \(14\)，大于 \(3\)，所以要继续探索 \(D\)，此时根的范围为 \([3, 14]\)

\(f\). \(D\) 的第二个叶节点的值为 \(5\)，还需要继续探索，第三个叶节点为 \(2\)，因此 \(D\) 的值为 \(2\)。

经过上述过程，\(MAX\) 在根节点的决策是走到值为 \(3\) 的 \(B\) 节点

---

\(\alpha-\beta\) 剪枝的名称取自描述这条路径上的回传值的两个参数：

• \(\alpha=\) 到目前为止路径上发现的 \(MAX\) 的最佳（即极大值）选择
• \(\beta=\) 到目前为止路径上发现的 \(MIN\) 的最佳（即极小值）选择

\(\alpha-\beta\) 搜索中需要不断更新 \(\alpha\) 和 \(\beta\) 值，并且当某个节点的值分别比当前的 \(MAX\) 的 \(\alpha\) 或者 \(MIN\) 的 \(\beta\) 值更差的时候裁剪该节点剩下的分支

\(\alpha-\beta\) 剪枝的效率很大程度上依赖于后继状态的次序。比如上面 \(e\) 和 \(f\)，因为先生成的最差后继，不会剪掉任何后续——这意味着应该先检查可能最好的后续

如果可以做到，则 \(\alpha-\beta\) 剪枝只需要检查 \(O(b^{\frac{m}{2}})\) 个节点来做出决策，这意味着有效分支因子为 \(\sqrt{b}\)，而不是 \(b\)；如果后继状态次序不是最佳的顺序，则要检查的节点数大概是 \(O(b^{\frac{3m}{4}})\)

5 局部搜索策略

5.1 局部搜索与最优化

与系统地搜索状态空间（保留各种路径）相对，不关心路径的搜索算法就是局部搜索算法

5.2 爬山法搜索

爬山法（hill-climbing）——就是向评价函数值减小的方向持续移动（反向登高过程） / 如果没有比当前状态更好的子状态（到达顶峰），则算法结束

一种局部贪婪搜索，优点在于能很快朝着解的方向进展。缺点在于：极易陷入局部最优值，因此该算法不具备完备性

5.3 模拟退火搜索

将爬山法和随机行走以某种方式结合，以同时获得完备性和效率

想象一个小球在滚动，如何晃动平面，晃动强度足以使小球弹出评价函数的局部极小值点，同时不会从全局极小值点出去

晃动强度：接受劣状态的概率

核心就是如何确定晃动强度

5.3.1 模拟退火算法解决思路

思路：开始使劲晃动（先高温加热）然后慢慢降低摇晃的强度（逐渐降温）[退火过程]

算法核心——选择移动

• 选择随机移动，如歌子状态更好，则 \(100\%\) 接受该子状态，否则以某个小于 \(1\) 的概率接受
• 接受概率是温度的函数：\(P=e^{\frac{\Delta E}{T}},\ \Delta E<0\)
  1. \(\Delta E\)：评价值变坏的梯度，与 \(P\) 成反比，该值越大意味着新评价值远低于旧评价值
  2. 温度 \(T\) 与 \(P\) 成正比

按照模拟退火思路，\(T\) 在算法迭代中逐渐减小。可以证明，如果 \(T\) 下降足够慢，那么模拟退火搜索将找到概率接近 \(1\) 的全局最优

5.3.2 模拟退火算法基本步骤

• 基本步骤

  给定初温 \(t=t_0\)，随机产生初始状态 \(s=s_0\)，令 \(k=0\)

  \(Repeat\)

  ​ \(Repeat\)

  ​ 产生新状态 \(s_j=Generate(S)\)

  ​ \(if\ min\{1,exp[\frac{-(C(s_j)-C(s))}{t_k}]\}\ge random[0,1]\) \(s=s_j\)

  ​ \(Until\) 抽样稳定准则满足

  ​ 退温 \(t_{k+1}=update(t_k)\) 并令 \(k=k+1\)

  \(Until\) 算法终止准则满足

• 影响优化结果的主要因素：三函数两准则 \(+\) 初温

5.3.3 模拟退火算法参数和操作设计

1. 状态产生函数
   • 原则：产生的候选解应遍布全部解空间
   • 方法：在当前状态的领域结构内以一定概率方式（均匀分布、正态分布、指数分布等）产生
2. 状态接受函数
   • 原则：在固定温度下，接受使目标函数下降的候选解的概率要大于使目标函数上升的候选解概率
   • 具体形式对算法影响不大，一般采用 \(min\{1,exp(\frac{-\Delta C}{t})\}\)
3. 初温
   • 初温越大，获得高质量解的机率越大，但花费的计算时间更多
   • 方法：数据差异度越大，初始温度越高
     1. 均匀抽样一组状态，以各状态目标值得方差为初温
     2. 随机产生一组状态，确定两两状态间的最大目标值差，根据差值，利用一定的函数确定初温
     3. 利用经验公式
4. 温度更新函数
   • 时齐算法的温度下降函数
     1. \(t_{k+1}=\alpha t_k,k\ge 0,0<\alpha<1\)，\(\alpha\) 越接近 \(1\) 温度下降越慢，且其大小可以不断变化
     2. \(t_{k}=\frac{K-k}{K}t_0\)，\(t_0\) 为初始温度，\(K\) 为算法温度下降总次数

5.3.4 模拟退火算法优缺点

• 模拟退火算法的优点：质量高；初值鲁棒性强；简单、通用、易实现
• 模拟退火算法的缺点：由于要求较高的初始温度、较慢的降温速率、较低的终止温度，以及各温度下足够多次的抽样，因此优化过程较长

5.4 遗传算法

遗传算法（generic algorithm / GA），一种重要的最优化方法，是进化算法的一种，借鉴生物界的进化规律(适者生存，优胜劣汰的种群进化遗传机制)

与剪枝搜索一样，遗传算法也是从 k 个随机状态开始——这 k 个状态称为种群，每个状态称为个体

• 个体编码：通常为向量表示

• 评价值：每个状态用其评价函数（适应度函数）给出评价值（适应值）

• 遗传操作包括选择、杂交、变异，来产生新一代种群，如此逐代进化，直到满足目标为止

5.4.1 遗传算法简要描述

1. 定义问题，状态的编码表示和适应度函数
2. 随机选择初始种群
3. 根据适应度函数，为每个个体计算适应值
4. 选择操作：为每个个体指定一个与其适应值成正比的被选择概率，根据概率选择两个个体
5. 杂交、变异操作：所选个体通过杂交/变异等操作产生新个体，加入种群，实现一次种群进化
6. 如果找到了解或者某种限制已到，则过程结束；否则转 \(3\)

5.4.1 遗传算法特点

• 遗传算法也结合了“上山”趋势和随机搜索，并在并行搜索线程之间交换信息
• 遗传算法的主要优势来自于杂交
  1. 杂交的优势在于它能够将独立发展的若干个相对固定的字符（能够执行有用的功能——“砖块”）组合起来，提高了搜索的粒度
  2. 所谓有用的砖块，就是几个结合起来可以构造问题的解

5.4.3 遗传算法模式

• 遗传算法上述特点可以用模式（schema）来解释——模式是某些位置上的数字尚未确定的一个状态子串
• 能够匹配模式的字符串称为该模式的实例
  1. 如果一个模式的实例的平均适应值超过均值，则种群内这个模式的实例数量会随时间而增长
  2. 遗传算法在模式和解的有意义成分相对应时才会工作得最好

举例：模式 \(*10101110\) 可以与 \(010101110\) 和 \(110101110\) 匹配；模式 \(*1010*110\) 可以和 \(010100110\)、\(010101110\)、\(110100110\)、\(110101110\) 匹配

模式定理：适应值高于群体平均值的模式在下一代的代表串数目将会增加，而适应值低于群体平均值的模式在下一代的代表串数目将会减少

积木块假设：长度较短、高于平均适应度的模式（积木块）在遗传算子的作用下，相互结合，能生成长度较长、适应度较高的模式

6 参考链接

【人工智能】— 博弈、极小极大值、α-β剪枝、截断测试

【人工智能】—局部搜索算法、爬山法、模拟退火、局部剪枝、遗传算法

人工智能第五章——对抗搜索（博弈搜索）