数据结构1.1-单调栈

一、简述

本节介绍一下单调栈以及单调栈的一些应用。

二、单调栈

所谓单调栈，就是具有存储的元素呈现某种单调性的栈。

比如：从栈底元素到栈顶元素是单调递减的，就是一个单调递减栈。

下面我们引入几道题目来更好的理解一下。

三、例题

1.[AcWing830.单调栈]

题目描述

给定一个长度为 \(N\) 的整数数列，输出每个数左边第一个比它小的数，如果不存在则输出 \(−1\)。

输入格式

第一行包含整数 \(N\)，表示数列长度。

第二行包含 \(N\) 个整数，表示整数数列。

输出格式

共一行，包含 \(N\) 个整数，其中第 \(i\) 个数表示第 \(i\) 个数的左边第一个比它小的数，如果不存在则输出 \(−1\)。

数据范围

\(1≤N≤10^5\)

\(1≤\) 数列中元素 \(≤10^9\)

输入样例

5
3 4 2 7 5

输出样例

-1 3 -1 2 2

解题思路

既然是介绍单调栈，那么我们肯定是使用单调栈来解决。具体思路：我们要输出每个数左边第一个小于它自己的数，我们构造一个单调单调递增的栈，首先我们从左往右遍历序列，当栈不空的时候，我们比较栈顶元素和当前数 \(a_i\) 的大小，如果栈顶元素大于等于 \(a_i\)，我们就弹出栈顶，直至栈为空或者不再满足为止，如果栈为空，说明 \(i\) 之前没有元素小于 \(a_i\)，就输出 \(-1\)，如果栈中还有元素，那当前的栈顶就是 \(i\) 左边第一个小于 \(a_i\) 的数。然后我们将 \(a_i\) 加到栈顶。

C++代码

#include <iostream>
using namespace std;
const int N = 100010;

int n, tt;
int stk[N];

int main()
{
    scanf("%d", &n);
    for(int i = 0; i < n; i ++)
    {
        int x;
        scanf("%d", &x);
        while(stk[tt] >= x && tt) tt --;
        if(tt == 0)
            printf("-1 ");
        else
            printf("%d ", stk[tt]);
        stk[++ tt] = x;
    }
    return 0;
}

2.[Daimayuan Online Judge.最大矩形面积]

题目描述

有一张 \(n\) 列的网格图，每列有一些格子被小蜗从底向上涂了色。现在给你每一列被涂色的格子的高度 \(a_i\)，请你求出被涂色的格子组成的最大矩形的面积。

输入格式

第一行一个整数 \(n\)，表示总列数。

接下来一行 \(n\) 个数 \(a_1,a_2,...,a_n\)。

输出格式

输出一行一个数，表示最大面积。

数据范围

对于 \(100\%\) 的数据，保证 \(1≤n≤2×10^5,1≤a_i≤10^9\)。

输入样例

5
1 2 5 3 4

输出样例

9

解题思路

具体思路：我们对于每一个 \(a_i\)，往其左边和右边找到小于 \(a_i\) 的第一个数所在的位置，分别是 \(l_i\) 和 \(r_i\)。那么对于这之间的矩形面积为 \((r_i - l_i - 1)*{a_i}\)。然后我们对于所有的矩形面积求最大值即可。

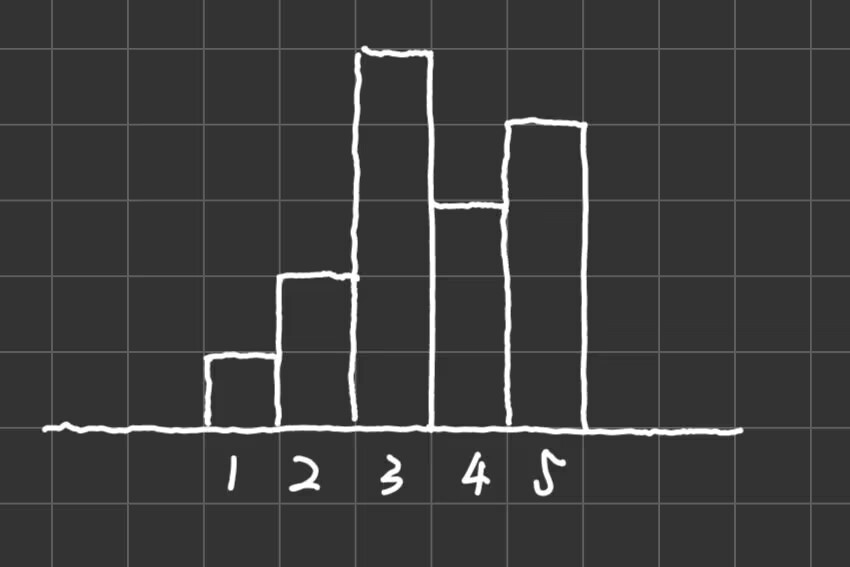
比如样例：对于 \(a_1,...,a_5\)，分别形成的矩形面积为 \(5、8、5、9、4\)，在枚举的时候我们可以看到其正确性：首先是尽可能往两边延伸，且可以覆盖在 \(a_i\) 情况下的最大面积。

C++代码

#include <bits/stdc++.h>
using namespace std;
const int N = 200010;

int n, a[N], stk[N], tt = 0;
int l[N], r[N];

int main()
{
	scanf("%d", &n);
	for (int i = 1; i <= n; i ++) 
		scanf("%d", &a[i]);
	for (int i = 1; i <= n; i ++)
	{
		while (tt && a[i] <= a[stk[tt]])
			tt --;
		if (tt)
			l[i] = stk[tt];
		else 
			l[i] = 0;
		stk[++ tt] = i;
	}
	tt = 0;
	for (int i = n; i >= 1; i --)
	{
		while (tt && a[i] <= a[stk[tt]])
			tt --;
		if (tt)
			r[i] = stk[tt];
		else 
			r[i] = n + 1;
		stk[++ tt] = i;
	} 
	long long ans = 0;
	for (int i = 1; i <= n; i ++)
		ans = max(ans, 1ll * abs(r[i] - l[i] - 1) * a[i]);
	cout << ans;
	return 0;
}

3.[码蹄集MT2036.移山造海]

题目描述

今天，无聊的小码哥打开了他的 \(tr\)，他突发奇想，“我要把一个新世界的一块大陆用水桶运水填成海”，尽管这个点子无聊透顶，但他真的去做了。

由于小码哥使用了修改器，他拥有无限的水桶。一个水桶的水能够填上一块格子。但如果倒入水后水位高于两边中一边土地，那么水会溢出，这桶水相当于没倒过。

另外，世界左右两侧是虚空，水碰到虚空会消失。

现在给了你这个世界的地形图，告诉你这个世界的宽度 \(n\) 以及每一列的土地的高度 \(h\)，问你至少要多少桶水才能将这个世界填满。

输入格式

第一行一个正整数 \(n\)。

第二行 \(n\) 个非负整数 \(h_i\)，表示第 \(i\) 列土地的高度。

输出格式

一个整数，表示至少需要几桶水。

数据范围

\(3≤n≤10000,0≤h≤10000\)

输入样例1

6
3 0 2 0 1 0

输出样例1

3

输入样例2

5
1 0 0 0 1

输出样例2

3

输入样例3

9
4 1 2 3 6 3 2 1 3

输出样例3

9

解题思路

最初的想法是记录所有的极大值点，然后计算两两相邻极大值间的水桶数，但是经同学的帮助，也想到了不适用的情况，比如 5 2 3 2 3 6 3 2 3 2 5 这种情况，答案就不对了。那么正确的思路应为：找到最大值的位置，往其左边和右边保存单调不增的序列，比如前面的例子最大值为 \(6\)，往左和往右是 \(5\)，然后在这之间进行填海操作。然后我们就可以使用单调栈了(碰巧今天复习了单调栈，就用到了这道题上)。

C++代码

#include <bits/stdc++.h> 
using namespace std;
const int N = 10010;

int n, h[N];
int stk[N], tt = 0;

int main()
{
    int Max = 0;
    scanf("%d", &n);
    for (int i = 1; i <= n; i ++) 
    {
        scanf("%d", &h[i]);
        if (h[i] > h[Max]) Max = i;
    }

    int ans = 0;
    // 左边
    for (int i = Max - 1; i >= 1; i --)
    {
        while (tt && h[i] >= h[stk[tt]])
            tt --;
        stk[++ tt] = i;
    }
    // 遍历左边
    for (int i = 1; i + 1 <= tt; i ++) 
    {
        int k = min(h[stk[i]], h[stk[i + 1]]);
        for (int j = stk[i + 1] + 1; j <= stk[i] - 1; j ++)
            ans += k - h[j];
    }
    for (int i = stk[1] + 1; i < Max; i ++)
        ans += min(h[stk[1]], h[Max]) - h[i];
    tt = 0;
    for (int i = Max + 1; i <= n; i ++)
    {
        while (tt && h[i] >= h[stk[tt]])
            tt --;
        stk[++ tt] = i;
    }
    for (int i = Max + 1; i < stk[1]; i ++)
        ans += min(h[stk[1]], h[Max]) - h[i];
    for (int i = 1; i + 1 <= tt; i ++)
    {
        int k = min(h[stk[i]], h[stk[i + 1]]);
        for (int j = stk[i] + 1; j <= stk[i + 1] - 1; j ++)
            ans += k - h[j];
    }
    cout << ans;
    return 0;
}