PyTorch中的梯度计算图（Computational Graph）的原理

PyTorch中的梯度计算图（Computational Graph）是其实现自动微分（Autograd）的核心机制，用于动态追踪张量操作并高效计算梯度。以下从原理与实现两个角度详细说明：

---

一、梯度计算图的核心原理

1. 动态有向无环图（Dynamic DAG）
   • 结构与组成：计算图由节点（张量或操作）和边（数据流向）构成。叶子节点（如用户创建的张量）通常是模型参数或输入数据，非叶子节点由前向传播中的运算生成。
   
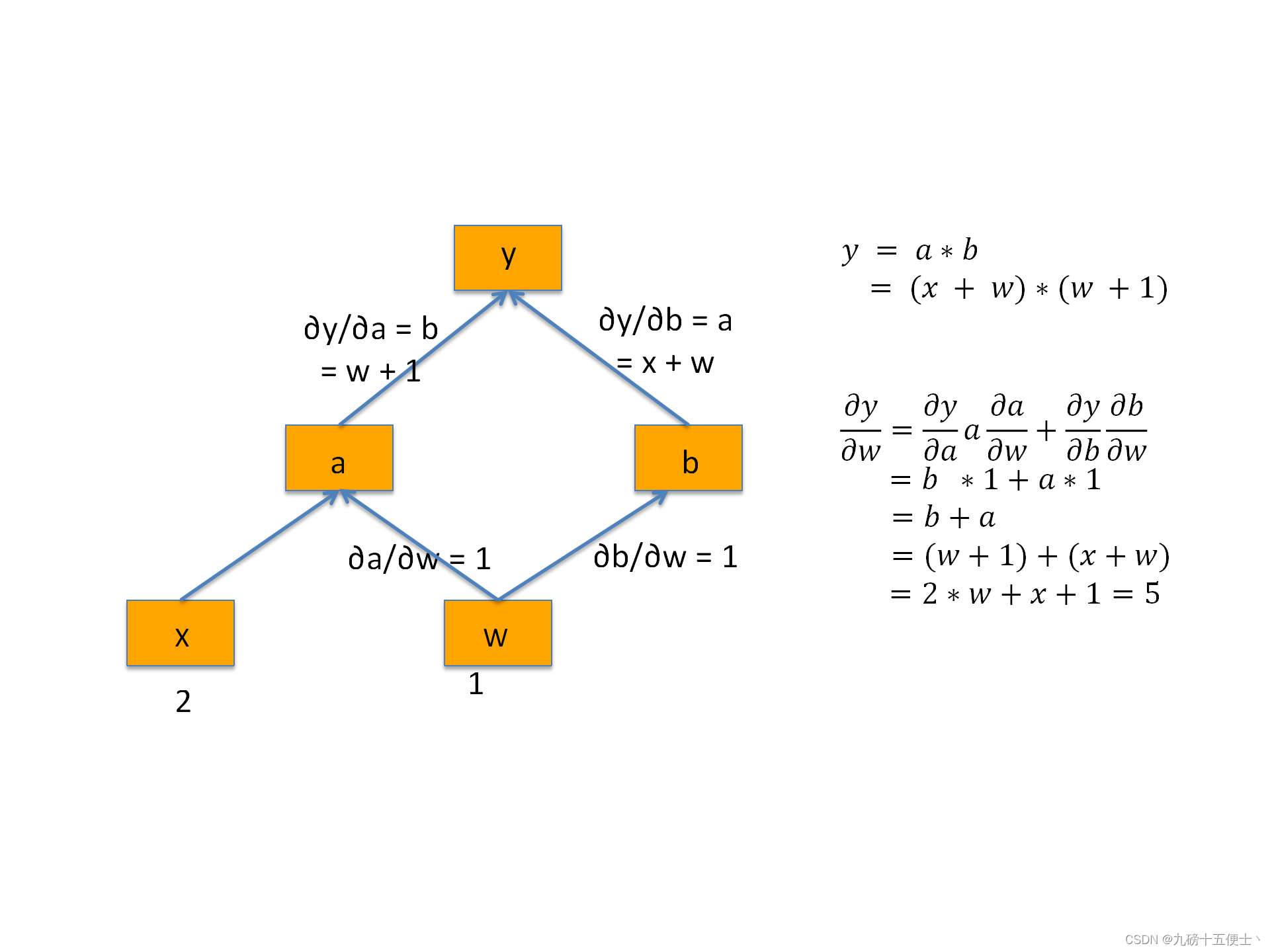
   • 动态性：PyTorch采用动态图机制，每次前向传播时会实时构建新的计算图，允许灵活处理条件分支、循环等复杂结构。

2. 自动微分与梯度记录
   • 梯度追踪：通过设置张量的requires_grad=True，PyTorch会记录所有相关操作，生成grad_fn属性（存储操作类型及输入信息）。

   • 反向传播：调用.backward()后，系统从输出节点开始，沿计算图反向应用链式法则计算梯度，结果存储在叶子节点的.grad属性中。

3. 梯度计算的灵活性
   • 标量与向量处理：默认仅对标量输出自动求导，向量需通过gradient参数指定方向向量（如y.backward(gradient=权重)）。

   • 梯度控制：通过torch.no_grad()禁用梯度追踪，或使用.detach()分离张量以节省内存。

---

二、实现机制与关键步骤

1. 前向传播与图构建
   • 当对requires_grad=True的张量执行操作（如加法、乘法）时，PyTorch会动态生成计算图，记录操作的grad_fn（如AddBackward、MulBackward）。

   • 示例：

   x = torch.tensor(2.0, requires_grad=True)
   y = x**2  # 生成PowBackward节点
   y.backward()  # 反向传播计算梯度
   print(x.grad)  # 输出4.0（即dy/dx=2x）
   

2. 反向传播与链式法则
   • 反向传播触发：调用.backward()后，从输出节点（如损失函数对应的标量）开始，按grad_fn回溯计算梯度。

   • 梯度累积与清零：默认梯度会累积，需在每次迭代前通过optimizer.zero_grad()手动清零，避免参数更新错误。

3. 动态图的优化特性
   • 内存效率：反向传播后，非叶子节点的中间梯度默认被释放，仅保留叶子节点的梯度。

   • 灵活调试：支持结合Python原生调试工具（如pdb）逐步检查计算图状态。

---

三、与其他框架的对比
PyTorch的动态图与TensorFlow的静态图（已弃用）形成对比：
• 动态图优势：适用于需要频繁修改网络结构（如RNN）、条件分支复杂的场景，且更易调试。

• 静态图劣势：需预先定义完整计算流程，灵活性较低，但可通过图优化提升计算效率。